4.2. Структурні середні

До середніх величин, окрім степеневих середніх, відносять також і структурні середні – моду і медіану.

Якщо для обчислення статечних середніх необхідно використовувати все наявні значення ознаки, то мода і медіана визначаються лише структурою розподілу. Тому їх і іменують структурними позиційними середніми. Мода і медіана характеризують величину варіанти, що займає певне положення ранжируваному варіаційному ряду. Моду і медіану часто використовують як середню характеристику в тих сукупностях, де розрахунок середньою статечною неможливий або недоцільний.

Модою називається значення ознаки, що зустрічається найчастіше, в одиниць даної сукупності.

Мода широко використовується в комерційній практиці і застосовується в тих випадках, коли потрібно охарактеризувати величину ознаки, що зустрічається найчастіше (наприклад, взнати розмір взуття, має найбільший попит, ціну на ринку, по якій було продано найбільшу кількість товару і так далі).

У дискретному варіаційному ряду мода відповідає найбільшій частоті спостережуваної ознаки.

Приклад. За даними таблиці. 4.5 про продажі взуттю визначити модальний розмір взуття.

Таблиця 4.5

Дані про продаж взуття

Розмір взуття	34	35	36	37	38	39	40
Число куплених пар	2	10	20	88	19	9	1

Модальний розмір взуття 37, оскільки взуттю цього розміру було продано більш всього – 88 пар (найбільша частота ознаки в дискретному варіаційному ряду).

У інтервальному ряду розподілу для обчислення моди необхідно визначити, в першу чергу, інтервал, в якому вона знаходиться, тобто модальний інтервал. Модальним інтервалом є інтервал, в якому спостережувана ознака має найбільшу частоту.

Для визначення моди в рядах з рівними інтервалами користуються наступною формулою:

(4.11)

де х₀ – нижній кордон модального інтервалу;

h– величина модального інтервалу;

f_mo – частота модального інтервалу;

f_mo-1 – частота інтервалу передування модальному;

f_mo+1 – частота інтервалу, наступного за модальним.

Приклад. Є група студентів, яка згрупована по росту таким чином (таблиця. 4.6).

Таблиця 4.6

Ріст студентів в групі

Групи росту, см. (х)	К-ть студентів, чіл. (f)	Накопичена частота (Sf)
160-165	3	3
165-170	7	10
170-175	16	26
175-180	10	36
180-185	9	45
185-190	3	48
190-195	2	50
Итого	50	–

Необхідно визначити модальне зростання – найбільш зростання студентів, що часто зустрічається. Як модальний приймаємо інтервал, в якому знаходиться зростання студентів в межах 170-175 см., оскільки в цьому інтервалі є 16 студентів – більшість. Тоді, модальне зростання студентів складе:

Мода – це саме те число, яке найчастіше зустрічається і в практиці має найширше вживання. Наприклад, за допомогою моди визначають тип покупця, що найбільш часто зустрічається. Або, наприклад, при вивченні попиту населення по певний розмір взуття, представляє інтерес визначення модального розміру, а середній розмір взуття, сам по собі, не має якого-небудь сенсу. У цих випадках, при характеристиці сукупності, як узагальнювальний показник перевага віддається моді, а не середньою арифметичною.

Медіаною називається те значення ознаки, яке знаходиться в середині варіаційного ряду і ділить його на дві рівні частини.

Якщо варіаційний ряд дискретний і містить непарне число варіант, то значення середньої ознаки в ряду і буде медіаною.

Наприклад: є наступні дані про стаж роботи (в літах) семи продавців: 1, 2, 2, 3, 5, 7, 10. Це дискретний варіаційний ряд з непарним числом варіант. У даному прикладі медіаною є четверта варіанта – 3 роки.

Якщо дискретний варіаційний ряд містить парне число варіант, то медіаною буде середня арифметична два суміжних варіант, таких, що знаходяться в центрі ряду.

Наприклад: бригада з шести продавців розподілена за стажем роботи (в роках) таким чином: 1, 3, 4, 5, 7, 9. Цей дискретний варіаційний ряд містить парне число варіант, центральними з яких є значення 4 і 5. Тоді медіана визначається як (4+5) /2=4,5 роки.

Для знаходження медіани в інтервальному варіаційному ряду необхідно спочатку визначити медіанний інтервал, тобто той інтервал, в якому знаходиться медіана. Медіанним називається такий інтервал, накопичена (кумулятивна) частота якого рівна або перевищує половину суми частот.

Для інтервального варіаційного ряду медіану визначають по формулі:

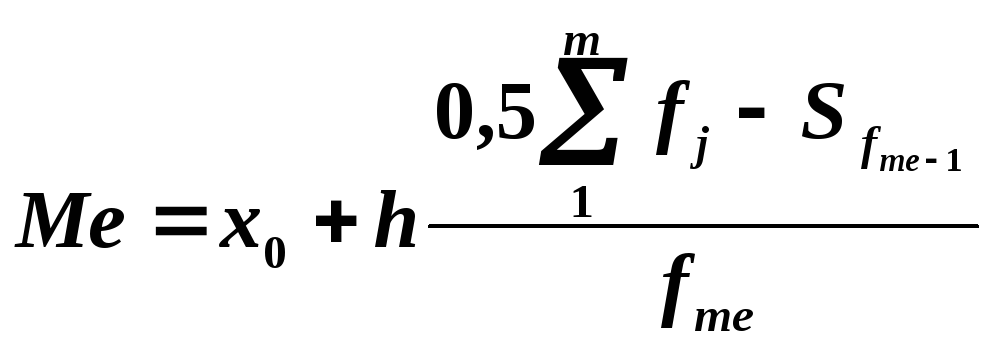(4.12)

де х₀ – нижній кордон медіанного інтервалу;

h – величина медіанного інтервалу;

–півсума частот медіанного інтервалу;

–кумулятивна частота (сума накопичених частот) перед медіанним інтервалом;

–частота медіанного інтервалу.

Приклад. повернемося до даних попереднього прикладу – угрупування студентів по росту. Визначимо медіанне зростання студентів. Як медіанний, приймаємо інтервал, в якому знаходиться зростання студентів в межах 170-175 см., оскільки накопичена частота в ньому , тобто перевищує половину суми частот . Тоді медіанне зростання студентів складе:

У розглянутому прикладі модальний і медіанний інтервали збігаються, то це лише окремий випадок. Часто модальний і інтервальний – різні інтервали.

Медіана також, в окремих випадках, має великі переваги перед середньою арифметичною. Якщо варіаційний ряд відносно невеликий, то на чисельне значення середньою арифметичною можуть робити впливи випадкові коливання крайніх варіант ряду, що ніяк не позначиться на значенні медіани. Наприклад, в інтервальному варіаційному ряду розподілу сімей по величині доходу, медіана буде найбільш прийнятній для аналізу статистичній сукупності.

Відмітимо, що відмінність між середньою арифметичною величиною, модою і медіаною зазвичай мале, якщо розподіл статистичних величин формою наближається до нормального закону.

При вивченні статистичної сукупності в деяких випадках самими розповсюдженими є мода і медіана і ось чому. На відміну від алгебри середніх, які значною мірою є абстрактною характеристикою статистичного ряду розподілу, мода і медіана виступають як конкретні величини, співпадаючі із сповна певними варіантами цього ряду. Це робить їх незамінними при вирішенні ряду практичних завдань. Так, при визначенні обсягу виробництва і реалізації найбільш ходових по розмірах товарів (взуття, одягу) було б дивним користуватися середньою арифметичною. Мода в цьому випадку найбільш відповідна величина. Медіана зручна у тому випадку, коли середнє значення ряду повинне мати певні конкретні характеристики. Наприклад, якщо ряд розподілу сімей по кількості членів сім'ї або ряд розподілу підприємств по мірі ритмічності їх роботи, то в цих випадках медіана (як, втім, і мода) буде переконливішою для аналізу.