
Дискретная математика - Лабораторная работа 5
.pdf
Лабораторная работа №5 НОРМАЛЬНЫЕ ФОРМЫ И ПОЛИНОМЫ
Цель: ознакомиться с нормальными формами булевых функций и формулами их представления, научиться преобразовывать булеву функцию при помощи дистрибутивных законов.
Теоретические сведения
Большое значение отводится в прикладных вопросах функциям двух переменных. Рассмотрим таблицу истинности этих функций.
Таблица 1 Основные логические операции
Обозначен |
Набор |
Другие |
Название |
|
|
|
|
|
ие |
истинности |
обозначения |
|
Булева |
||||
логической |
Чтение |
|||||||
логической |
значений |
логической |
формула |
|||||
операции |
|
|||||||
операции |
|
операции |
|
|
|
|
||
|
|
|
|
|
|
|||
0 |
0000 |
0 |
Константа 0 |
любое 0 |
0 |
|
||
|
0001 |
|
Конъюнкция, |
|
|
|
|
|
х1 х2 |
|
х1 & x2 |
логическое |
х1 и х2 |
x1x2 |
|||
|
х1·х2, |
умножение, |
||||||
|
|
|
|
|
|
|||
|
|
|
логическое «И» |
|
|
|
|
|
х1 ← х2 |
0010 |
х1 х2 |
Отрицание |
х1, но не |
|
|
|
|
x1 x2 |
||||||||
|
|
х1 х2 |
импликации |
х2 |
||||
х1 |
0011 |
х1 |
Повторение х1 |
как х1 |
x1 |
|||

х2 ← х1 |
0100 |
х2 х1 |
Отрицание |
х2, но не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
обратной |
|
|
|
|
|
|
|
|
x1x2 |
|||||||||||||||||||||||||||
|
|
|
|
|
х2 х1 |
х1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
импликации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
0101 |
x2 |
Повторение x2 |
как x2 |
|
|
|
|
|
|
|
|
|
|
x2 |
|||||||||||||||||||||
|
|
|
|
0110 |
|
|
|
|
|
|
|
|
|
Сумма по модулю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разделительная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 х2 |
|
|
|
|
|
|
|
|
|
|
или х1, |
|
x1 x2 x1 x2 |
||||||||||||||||||||||||
|
х1 ≡ х2 |
дизъюнкция, |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
или х2 |
(x1 x2 )(x1 x2 ) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разделительное |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«ИЛИ», |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неравнозначность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0111 |
|
|
|
|
|
|
|
|
|
Дизъюнкция, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
логическое |
|
|
|
|
|
|
|
x1 x2 |
|||||||||||||||
х1 х2 |
|
х1 + х2 |
сложение, |
х1 или х2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
логическое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«ИЛИ» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
Стрелка Пирса, |
не х1 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 ↓ х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x1 |
||||||||||||||||||||
, x1 x2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
функция Вебба |
не х2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2 |
||||||||||
х1 х2 |
|
|
|
|
|
|
|
|
|
Эквиваленция; |
х1 как х2 |
|
|
x1 |
x2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Равнозначность |
(x1 |
|
|
|
)( |
|
x2 ) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
x1 |
||||||||||||||||||||||||||
|
|
|
|
1010 |
¬x2 , |
|
|
|
|
Отрицание х2 |
не х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x2 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|||||||||||||||||||||
|
|
|
|
1011 |
х2→х1 |
|
если х2, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
х2→х1 |
|
Обратная |
х1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
х2 х1 |
|
|
|
|
|
x1 x2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
Импликация |
из х2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
х2 х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
следует х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1100 |
¬x1 , |
|
|
Отрицание х1 |
не х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x1 |
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
||||||||||||||||||||
|
|
|
|
1101 |
х1 → х2 х1 |
|
если х1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
х2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
х1 → х2 |
|
х2 |
Импликация |
|
|
|
|
|
|
x1 x2 |
|||||||||||||||||||||||||||
|
из х1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
х1 х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
следует х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
|
|
|
|
|
|
Штрих Шеффера |
не х1 или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1|х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 x2 |
||||||||||||||||||||||
х1 х2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
не х2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1111 |
1 |
|
|
|
|
|
|
Константа 1 |
любое 1 |
1 |
|
|
|
|
|
|
|
|||||||||||||||||

Ход работы
Задание 1
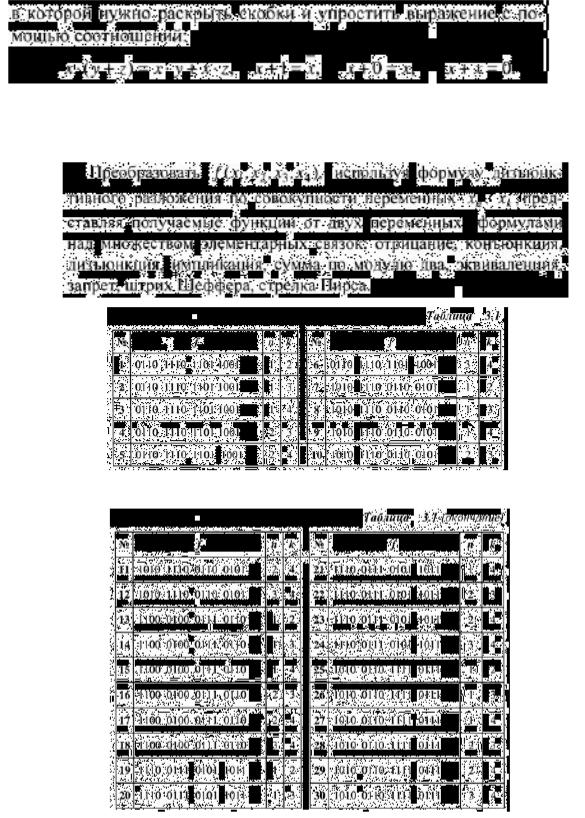
Варианты заданий взять из таблицы 3.1 в соответствии с номером по списку в журнале.
Пример выполнения задания 1:


Задание 2
Варианты заданий взять из таблицы 3.2 в соответствии с номером по списку в журнале.
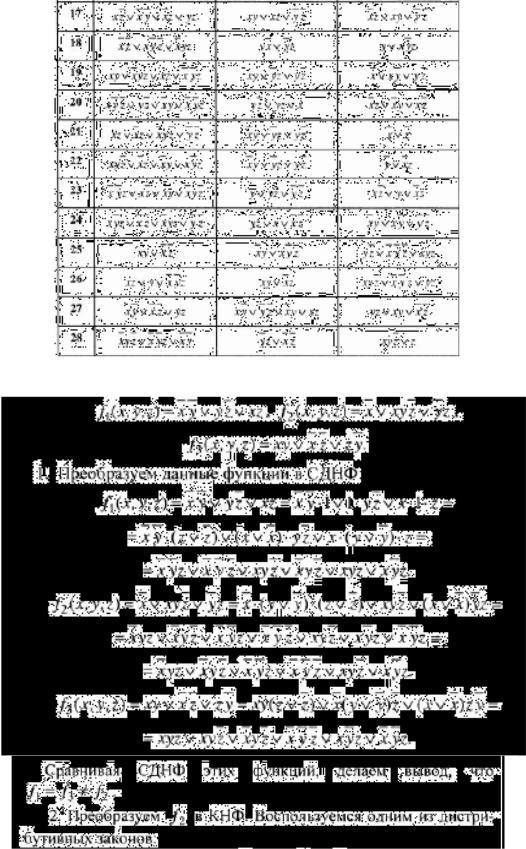
Пример решения задания 2:

Содержание отчёта:
1)Номер, тема и цель лабораторной работы.
2)Решение заданий № 1, 2 в соответствии со своим вариантом.
3)Вывод.
