МУ до ПЗ КЛ 2012 укр вер 2 семестр (2)

52

6.4Контрольні запитання

1.Які елементи пам'яті прийнято називати тригерами?

2.Які тригери називаються бістабільними?

3.Як виглядає узагальнена схема тригерного пристрою?

4.Як виглядає схема RS-тригера в базисі «І-АБО-НІ»?

5.Як виглядає схема RS-тригера, який має парафазні виходи ?

7 ЗАБЕЗПЕЧЕННЯ СТІЙКОСТІ ФУНКЦІОНУВАННЯ ЦИФРОВИХ АВТОМАТІВ

7.1 Мета заняття

Провести аналіз причин появи гонок в автоматах, засвоєння апаратних та алгоритмічних способів боротьби з явищем гонок в автоматах, рішення задач протигоночного кодування станів автомата.

7.2 Короткі основні відомості з теорії та вирішення типових завдань

7.2.1.Гонки в автоматі

Завдання кодування станів є однією з основних задач канонічного методу структурного синтезу автоматів. Кодування полягає у встановленні взаємнооднозначної відповідності між множиною А = {а1,. . . , ам} станів автомата і множиною R-компонентних векторів {К1,. . . , КМ}, Кm = (еm1, ..., emR), де еmr - стан r-го елементу пам'яті, r = 1,. . . , R. Якщо еmr {0, 1}, тобто алфавіт станів елементів пам'яті двійковий, R ] log2M [. Далі заради простоти обмежимося використанням в якості елементів пам'яті RS-тригерів, які будемо позначати

T1,. . . , ТR.

Перехід автомата з одного стану в інший здійснюється за рахунок зміни станів елементів пам'яті. Так, якщо автомат переходить зі стану аm з кодом 0101

53

в стан аs з кодом 1001, то це означає, що тригер Т1 переходить зі стану 0 в стан 1, тригер Т2 - зі стану 1 у стан 0, а стану тригерів Т3 і Т4 НЕ змінюються.

При функціонуванні автомата можуть з'явитися так звані змагання. Явище змагань виникає внаслідок того, що елементи пам'яті мають різні, хоча і досить близькі, часи спрацьовування. Крім того, різні також затримки сигналів збудження, що надходять на вхідні канали елементарних автоматів по логічним ланцюгах неоднакової довжини. Якщо при переході автомата з одного стану в інший повинні змінити свої стани відразу декілька запам'ятовуючих елементів, то між ними починаються змагання. Той елемент, який виграє ці змагання, тобто змінює свій стан раніше, ніж інші елементи, може через ланцюг зворотного зв'язку змінити сигнали на входах деяких запам'ятовуючих елементів до того, як інші елементи, які приймають участь у змаганнях, змінять свої стани. Це може призвести до переходу автомата в стан, не передбачений його графом. Тому в процесі переходу зі стану аm в стан аs під дією вхідного сигналу zf (рис. 7.1, а) автомат може опинитися в деякому проміжному стані аk або аl в залежності від того, який елемент пам'яті виграє змагання. Якщо потім при тому ж вхідному сигналі автомат з ak і al перейде в стан аs, то такі змагання є допустимими, або некритичними. Якщо ж в цьому автоматі є перехід, наприклад, з аk в aj as під дією того ж сигналу zf (рис. 7.1, б), то автомат може перейти в aj, а не в as і правильність його роботи тим самим буде порушена. Такі змагання називаються критичними змаганнями або гонками. При кодуванні станів гонки повинні бути усунені. Кодування з усуненням гонок називається протигоночним.

Рис. 7.1. Змагання між елементами пам'яті а) некритичні, б) критичні.

Один із способів ліквідації гонок полягає в тактуванні вхідних сигналів автомата імпульсами певної тривалості. Передбачається, що крім вхідних

54

каналів x1,. . . , хL є ще один канал С від генератора синхроімпульсів (ГСІ), по якому надходить сигнал С = 1 в момент приходу імпульсу і С = 0 при його відсутності. У зв'язку з цим вхідним сигналом на переході (am, as) буде не zf, a Сzf. Тоді, якщо тривалість імпульсу tС менше самого короткого шляху проходження тактованого сигналу зворотного зв'язку по комбінаційній схемі, то до моменту переходу в проміжний стан ak (рис. 7.1, б) сигнал С дорівнює нулю і, отже, Сzf = 0, що виключає гонки.

Інший спосіб ліквідації гонок полягає у введенні подвійної пам'яті (рис. 7.2). У цьому випадку кожен елемент пам'яті дублюється, причому перепис з нижнього елемента пам'яті в верхній відбувається в момент відсутності тактуючого імпульсу (С=0). Сигнали зворотного зв'язку для одержання функції збудження і функцій виходів автомата знімаються з верхнього ряду тригерів. Таким чином, змагання можуть виникнути тільки між нижніми тригерами, сигнали зворотного зв'язку не зможуть змінитися до тих пір, поки С не стане рівним нулю. Але тоді вхідний сигнал Сzf, також дорівнює нулю, а тому гонок бути не може.

Рис. 7.2. Подвійна пам'ять

7.2.2 Протигоночне кодування.

Суть і алгоритм розв'язування станів

Нехай (, ) і (, ) - дві пари двійкових кодів довжини R. Ці пари будуть називатися розв'язаними, якщо при деякому I (1 i I) i-розряд коду приймає значення 1 на парі (,) і протилежне значення на парі (,). Якщо це не дотримується, пари називаються зв'язаними.

55

Теорема. В автоматі, стан якого закодовано двійковими кодами кінцевої довжини, гонки відсутні тоді і тільки тоді, коли для будь-яких двох переходів (am, as) і (ak, al) при as al, що відбуваються під дією одного і того ж вхідного сигналу відповідні пари розв'язані.

Алгоритм протигоночного кодування заснований на цій теоремі, ідея полягає в наступному: послідовно переглядаючи всі пари переходів, що мають хоча б 1 загальний вхідний сигнал, який здійснює ці переходи, слід присвоювати розрядам кодів такі значення, щоб ці пари кодів станів були розв'язані.

Нехай (am, as) і (ak, al) пари переходів автомата, а , , , - відповідно четвірка кодів станів am, as, ak, al довжини i.

Примітка. Четвірка кодів, , , складається із 0, 1 і Х.

Алгоритм розв'язування пар:

1.Якщо при деякому r (1 r R) значення r-розряду четвірки , , , , утворюють набір 0011, пара переходів вважається розв'язаною і переходить до наступної пари.

2.Якщо при деякому r (1 r R) значення r-розряду четвірки , , , , утворює один з наборів

слід довизначити невизначені значення r-розряду четвірки так, щоб його значення утворили набір 0011. Перехід до наступної пари.

3.Якщо при деякому r (1 r R)) значення r-розряду четвірки , , , , утворює набір 1100, пара вважається розв'язаною. Перехід до наступної пари.

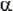4.Якщо при деякому r (1 r R) значення r-розряду четвірки , , , утворює один з наборів

56

слід довизначити невизначені значення r-розряду четвірки так, щоб його значення утворили набір 1100. Перехід до наступної пари.

В результаті розв'язування пар переходів довжина коду виявляється не мінімальною, тому при введенні нового розряду можуть бути розв'язані пари, які були розв'язані раніше. Отже алгоритм протигоночного кодування передбачає мінімізацію довжини одержуваних кодів станів. Суть полягає в наступному: виключається 1 з розрядів кодів, в результаті чого деякі пари можуть виявитися зв'язаними. Застосовують алгоритм розв'язування. Виключають ще 1 розряд. Знову застосовують алгоритм розв'язування. І так до тих пір поки довжина коду не перестане зменшуватися. Якщо в результаті роботи алгоритму деякі значення розрядів буду невизначені, то їх визначають довільно.

7.2.3.Приклад протигоночного кодування

1.Розв'язання пар переходів

Розглянемо алгоритм протигоночного кодування на прикладі автомата, функція переходів якого задана таблицею (Табл. 7.1).

Таблиця. 7.1

Пари переходів, які відбуваються під дією сигналів z1, z2, z3 утворюють масиви М1, М2, М3.

М1 = ((а1, а2), (а2, а2), (а3, а4), (а4, а4), (а5, а6), (а6, а6)). М2 = ((а1, а1), (а2, а3), (а3, а3), (а4, а1), (а5, а3)).

М3 = ((а2, а5), (а3, а7), (а5, а5), (а7, а7)).

Починаємо розв'язувати пари з М1. Перехід (а1, а2) з (а2, а2) розв'язувати не треба, тому що стани а2 і а2 співпадають. Пару переходів (а1, а2) і (а3, а4) будемо розв'язувати введенням змінної 1, як в (Табл. 7.2).

Таблиця. 7.2