12.4. Модель экономического роста р. Солоу

В модели Солоу центральное место отводится технологическому прогрессу, который обеспечивает непрерывный экономический рост. К другим моделям данного направления относится однофакторная модель Домара-Харрода. В этой модели рост продукта связывается с нормой эффективностью накопления. Центральное уравнение этой модели имеет следующий вид: у=ав, где (1)

У – темп прироста продукта, а – норма накопления, в – эффективность накопления (коэффициент капиталоотдачи).

При вычислении нормы накопления (а) следует учесть, что, во-первых часть накопления осуществляется за счет амортизационного фонда и используется для возмещения выбытия основного капитала, во-вторых, из фонда накопления обеспечивается вложение не только в основной, но и в оборотный капитал, включая резервы.

Неоклассическая модель в условиях равновесия между спросом и предложением учитывает изменчивость коэффициента капиталоотдачи. Соотношение "капитал – производство" становится гибким вследствие того, что неоклассические модели учитывают не один, а два производственных фактора и допускают их взаимозаменяемость. Допуская различные комбинации производственных факторов, можно добиться роста объемов производства даже при той же технике. Среди аналитических инструментов неоклассических моделей главное место занимает производственная функция: У=f(K,L), где У- продукт, а К и L – затраты на капитал и труд. Объем и динамика продукта связывается с объемом и динамикой совокупных затрат и их эффективностью: или Y = abk+где d – коэффициент, отражающий соотношение величин факторов К и L к величине продукта У;

b и - параметры функции, характеризующие эластичность объемов и динамики продукта от затрат факторов производства, т.е. параметры, показывающие насколько увеличится объем производства, если любой производственный фактор увеличится на 1%;

Ки П- темпы роста соответственно капитала и труда.

Модель Солоу имеет возможность описать эти изменения в динамике, т.е. делает его более похожим на фильм, чем фотографию. Модель роста Солоу показывает, как сбережения, рост населения и технологический прогресс воздействуют на рост объема производства во времени.

Модель дает основу, с помощью которой можно проанализировать один из наиболее важных вопросов экономики: какая часть производственного продукта должна потребляться сегодня, и какая часть его должна сберегаться для использования в будущем. Поскольку сбережения равны инвестициям, сбережения определяют объем капитала, которым экономика будет располагать в будущем.

Предложение товаров в модели Солоу описывается с помощью известной производственной функции: Y=F (K,L), где К – капитал, L-труд.

Т.е. объем производства зависит от запасов капитала и используемого труда. Модель Солоу предполагает, что производственная функция обладает свойством постоянной отдачи от масштаба.

Производственная функция с постоянной отдачей от масштаба удобна для этой цели, потому что объем производства на одного рабочего зависит тогда от количества капитала, приходящегося на одного работника.

Производственную функцию можно записать так у=f(k), где f(k)=F (k,1). На рис. Изображена эта производственная функция

У f(k) Закон убывающей эффективности

Выпуск (аналогия).

на одного

работника МРК

1

капитал на одного работника К

Тангенс угла наклона данной производственной функции показывает, сколько дополнительного продукта на одного работника можно получить, если увеличить капиталовооруженность на одну единицу. Эта величина является предельным продуктом капитала МКР. Это можно записать так:

МКР = f(k + 1) - f(k). Заметим, что по мере роста капиталовооруженности график производственной функции становится более пологим, т.е. угол наклона уменьшается. Такая производственная функция характеризуется понижающейся предельной производительностью капитала: каждая дополнительная единица капитала производит меньше продукта, чем предыдущая. Когда запас капитала на одного работника невелик, каждая дополнительная единица капитала дает большую отдачу. Если же капиталовооруженность труда высокая, то дополнительная единица капитала менее эффективна и дает меньше дополнительной продукции.

В модели Солоу спрос предъявляется со стороны потребителей и инвесторов. Иными словами, продукция произведенная каждым рабочим, делится между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного рабочего: У=с+I, где с – потребление, I – инвестиции.

Модель Солоу предполагает, что функция потребления принимает простую форму C = (1 – S)·у, где норма сбережения S принимает значения от 0 до 1. Эта функция означает, что потребление пропорционально доходу. Каждый год часть (1 – S) дохода потребляется и часть S сберегается.

Роль такой трактовки потребления выяснится, если мы заменим величину C величиной (1 – S)·у в тождестве национальных счетов: у =(1 – S)·у + I. После преобразования получим: I = S·у. Это уравнение показывает, что инвестиции (как и потребление) пропорциональны доходу. Если инвестиции равны сбережениям, норма сбережений S показывает, какая часть произведений продукции направляется на капитальные вложения.

Представив две главных составляющих модели Солоу – производственную функцию и функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост. Запасы капитала могут изменяться по двум причинам: 1. Инвестиции приводят к росту запасов капитала. 2. Часть капитала изнашивается, то есть амортизируется, что приводит к уменьшению запасов капитала. Для того, чтобы понять, как изменяются запасы капитала, необходимо найти факторы, определяющие величину инвестиций и амортизации. Инвестиции в расчете на одного работника являются частью продукта, приходящегося на одного работника (S·y). Заменив y выражением производственной функции, мы представим инвестиции на одного работника как функцию от капиталовооруженности: I = S·f(k).

Чем выше уровень капиталовооруженности k, тем выше объем производства f(k) и больше инвестиции I. Это уравнение, которое включает в себя производственную функцию и функцию потребления, связывает существующие запасы капитала k с накоплением нового капитала i. На графике показано, как норма сбережений определяет разделение продукта на потребление и инвестиции для каждого из значений k.

У Производительность f(k)

С Sf(k)

у

i

капиталовооруженность k

Норма сбережений S определяет деление производственного продукта на потребление и инвестиции. Для любого уровня капиталовооруженности k объем производства есть f(k), инвестиции равны S·f(k), а потребление составляет f(k) – S·f (k).

Предположим, что ежегодно выбывает определенная доля капиталаσ. Назовем σ нормой выбытия. Например, если капитал эксплуатируется в среднем 25 лет, то норма выбытия равна 4% в год (σ= 0,04). Таким образом, количество капитала, которое выбывает каждый год, cоставляет σ·k. На графике показано, как выбытие зависит от запасов капитала.

σ К

Выбытие

σ к

Капиталовооруженность

Влияние инвестиций и выбытия на запасы капитала можно выразить с помощью следующего уравнения:

Изменение запасов капитала =инвестиции – выбытие, т.е. к=I-σк, где к есть изменение запасов капитала, приходящихся на одного работника за год. Поскольку инвестиции равны сбережениям, изменение запасов капитала может быть записано так: к=Sf(к)- σк. Это уравнение показывает, что изменение запасов капитала равно инвестициям Sf(к) минус выбытие капитала σк.

Чем выше капиталовооруженность, тем больше объем производства и инвестиции, приходящиеся на одного работника. Однако, чем больше запасы капитала, тем больше и величина выбытия.

На рис. показано, что существует единственный уровень капиталовооруженности, при котором инвестиции равны величине износа. Если в экономике достигнут именно такой уровень, то он не будет меняться во времени, поскольку две действующие на него силы (инвестиции и выбытие) точно сбалансированы. Таким образом, при данном уровне капиталовооруженности . Назовем эту ситуацию состоянием устойчивой капиталовооруженности и обозначим его k^*.

Предположим, что запасы капитала в начальном состоянии превышают k^*, например, в точке k₂. В этом случае инвестиции меньше, чем выбытие: капитал выбывает быстрее, чем добавляется. Таким образом, капиталовооруженность будет сокращаться, опять приближаясь к устойчивому уровню. В момент, когда запасы капитала, приходящиеся на одного работника, достигнут устойчивого уровня, инвестиции сравняются с выбытием, и капиталовооруженность не будет ни расти, ни падать.

Предположим, что экономика начинает развиваться, находясь в устойчивом состоянии при норме сбережений S₁ и запасах капитала k₁^*. Норма сбережений затем возрастает с S₁ до S₂, вызывая соответствующий сдвиг вверх кривой Sf(k). При начальном уровне сбережений S₁ и начальных запасах капитала k₁^*,

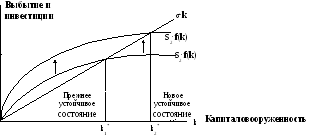
инвестиции как раз компенсирует выбытие капитала. Сразу после повышения нормы сбережений инвестиции увеличиваются, но запас капитала, и следовательно, выбытие остаются пока неизменными; в итоге инвестиции превышают выбытие. Капитал будет постепенно расти до тех пор, пока экономика не достигнет нового устойчивого состояния k₂^* с большой капиталовооруженностью и более высокой производительностью труда, чем в прежнем устойчивом состоянии.

Модель Солоу показывает, что норма сбережений является ключевой (определяющей) детерминантой величины устойчивой капиталовооруженности. Если норма сбережений более высока, то экономика будет иметь при прочих равных условиях больший запас капитала и более высокий уровень производства.

Более высокие сбережения ведут к более быстрому росту, но это ускорение длится не вечно. Увеличение нормы сбережений обеспечивает рост до тех пор, пока экономика не достигнет нового устойчивого состояния. Если в экономике поддерживается высокая норма сбережений, то и капиталовооруженность, и производительность будут высоки, но и сохранить высокие темпы экономического роста навечно не удастся.

В соответствии с моделью Солоу страна, которая направляет значительную часть дохода на сбережения, будет иметь высокую устойчивую капиталовооруженность труда и, вследствие этого, высокий уровень душевого дохода. Страны с высоким уровнем инвестиций (США, Канада или Япония) обычно имеют высокий душевой доход, в то время как страны с низким уровнем инвестиций (Эфиопия, Заир, Чад) имеют низкий доход на душу населения. Международный опыт, таким образом, подтверждает предсказания модели Солоу о том, что норма сбережений является важнейшей детерминантой богатства или бедности страны.

Теперь рассмотрим вопрос: какие размеры накопления являются оптимальными.

Уровень накопления капитала, обеспечивающий устойчивое состояние с наивысшим уровнем потребления, называется Золотом уровнем накопления капитала, или "Золотым правилом" Э.Фелпса, и обозначается k^**.

Устойчивый уровень потребления есть разница между выпуском и выбытием капитала в устойчивом состоянии. Оно показывает, что увеличивающаяся капиталовооруженность двояко воздействует на величину потребления: она способствует росту выпуска продукции, но в то же время большее количество продукции требуется для возмещения выбытия капитала. На рис. выпуск продукции и выбытие в устойчивом состоянии показаны в виде функции от устойчивой капиталовооруженности. Потребление в устойчивом состоянии – это разница между объемом производства и выбытием капитала. Рисунок показывает, что существует единственный уровень капиталовооруженности – уровень Золотого правила k^**, при котором душевое потребление достигает максимума.

Если капиталовооруженность меньше ее уровня по Золотому правилу, то рост запасов капитала вызывает рост производства, превышающий увеличение выбытия. В этом случае потребление растет. Кривая производственной функции наклонена круче, чем линия σk^**, так что расстояние между ними (равное потреблению) растет по мере увеличения k^*. С другой стороны, если объем капитала превышает уровень Золотого правила, дальнейший рост капиталовооруженности уменьшит потребление, так как рост выпуска продукции окажется меньше прироста выбытия капитала.

При капиталовооруженности, соответствующей уровню Золотого правила, производственная функция и линия σk^* имеют одинаковый наклон, и потребление достигает максимального уровня.

Если же устойчивый запас капитала превышает уровень Золотого правила, то рост объема капитала снижает потребление, поскольку предельный продукт капитала меньше, чем норма выбытия. Поэтому следующее условие составляет само Золотое правило МРК = σ. При капиталовооруженности на уровне Золотого правила предельный продукт капитала равен норме выбытия. Другими словами, если Золотое правило выполняется, предельный продукт за вычетом нормы выбытия, МРК = σ, равен нулю.

Базовая модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост. Высокий уровень сбережений временно увеличивает темпы роста, но экономика в конце концов приближается к устойчивому состоянию, при котором запасы капитала и объем производства постоянны. Для того, чтобы объяснить непрерывный экономический рост, который наблюдается в большинстве стран мира, нужно расширить модель Солоу и включить в нее два других источника экономического роста: рост населения и технологический прогресс.

Рост численности работников ведет к сокращению капиталовооуженности каждого из них. Изменение запаса капитала, приходящегося на одного работника, составит: k = I – σ·k – n·k. Три составляющих в правой части этого уравнения показывают влияние инвестиций, выбытия капитала и роста населения на величину капиталовооруженности. Инвестиции увеличивают k, а выбытие капитала и рост населения уменьшает ее. Для того, чтобы воспользоваться этим равенством, заменим I на S f(k) и перепишем его: k = S f(k) - (σ + n)·k. Эффекты выбытия капитала и роста населения теперь объединены. Уравнение показывает, что рост населения уменьшает капиталовооруженность таким же образом, как и выбытие. Выбытие уменьшает k за счет сокращения запасов капитала, в то время как рост населения уменьшает k, распределяя капитал между большим количеством работающих.

Для того, чтобы экономика была в устойчивом состоянии, инвестиции S f(k), должны компенсировать последствия выбытия капитала и роста населения – (σ + n)·k, что представлено на рис. точкой двух кривых.

Инвестиции

(σ+n)·k

S·f(k)

k*

k Капиталовооруженность

Устойчивый уровень

Рост населения дополняет исходную модель Солоу по трем направлениям. Во-первых, он позволяет приблизиться к объяснению причин экономического роста. В устойчивом состоянии экономики при растущем населении капитал и выпуск продукции на одного работника остаются неизменными, но поскольку количество работников растет с темпом n, капитал и объем производства тоже растут с темпом n. Следовательно, рост населения не может объяснить длительного роста уровня жизни, поскольку объем производства в расчете на одного работника в устойчивом состоянии остается постоянным. Однако рост населения может объяснить непрерывный рост валового выпуска продукции.

Во-вторых, рост населения позволяет дать дополнительно объяснение того, почему некоторые страны богаты, а другие – бедны.

Так модель Солоу предсказывает, что страны с более высокими темпами роста населения будут иметь более низкий ВНП на душу населения.

Инвестиции

(σ + n2)·k

(σ + n1)·k

S·f(k)

k₂^* k₁^* k

Капиталовооруженность

В-третьих, рост населения влияет на уровень накопления капитала по Золотому правилу. Вспомним, что потребление на одного работника равно с = у - i. Поскольку устойчивый объем производства есть f(k^*), а инвестиции устойчивого состояния – это (σ + n)·k^*, устойчивый уровень потребления можно определить как с^*= f(k^*) - (σ+n)·k^*. Уровень k^*, который максимизирует потребление, таков, что МРК = σ + n, или соответственно МРК – σ = n. В устойчивом состоянии по Золотому правилу предельный продукт капитала минус норма выбытия равен темпу прироста населения.

Теперь включим в модель Солоу технологический прогресс – третий источник экономического роста. Запишем производственную функцию следующим образом: Y = F(K,L х Е), где Е представляет собой новую переменную, которую мы назовем эффективностью труда одного работника. Эффективность труда зависит от здоровья, образования и квалификации рабочей силы.

Описание технологического прогресса через приращение эффективности труда делает его аналогичным росту населения.

Уравнение, показывающее изменение к с течением времени, теперь выглядит следующим образом: Новый элемент этой формулы g, темп технологического прогресса, появляется постольку, поскольку к есть количество капитала в расчете на единицу труда с постоянной эффективностью. Если величина g велика, то общее количество единиц труда с постоянной эффективностью растет быстро, а прирост капитала на такую единицу труда сравнительно мал и может стать отрицательным.

Таким образом, с учетом технологического прогресса наша модель в конце концов может объяснить, почему уровень жизни растет из года в год. Тем самым мы показывали, что технологический прогресс может поддерживать непрерывный рост выпуска продукции на одного работника, тогда как высокий уровень сбережений ведет к высоким темпам роста только до момента достижения устойчивого состояния. Как только экономика достигает устойчивого состояния, темп роста производства на одного работника зависит только от скорости технологического прогресса. Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущий уровень жизни.

Введение в модель технологического прогресса изменяет также условия выполнения Золотого правила. Золотое правило для накопления капитала определяет устойчивый уровень, при котором максимизируется потребление на единицу труда с постоянной эффективностью. Следует сказать, что устойчивый уровень потребления на единицу труда с неизменной эффективностью составляет: .

Устойчивый уровень потребления максимизируется, если:

МРК – σ + n + g, или МРК – σ = n + g. Таким образом, при запасе капитала по Золотому правилу чистый предельный продукт капитала (МРК – σ) равен темпу прироста объема производимой продукции n + g.