Лабораторная работа №1

“Электрооптический эффект в кристаллах”

Цель работы: изучить теорию электрооптических эффектов в кристаллах. Для кристалла KDP выбрать схему опыта для измерения линейных электрооптических коэффициентов и рассчитать соответствующие полуволновые напряжения.

Ход работы

1. Записываем уравнение оптической индикатрисы для кристалла без поля.

2. Записываем уравнение индикатрисы при произвольно ориентированном внешним электрическом поле Е = Е₁, Е₂, Е₃).

3. Для различных (X, Y, Z и др.) срезов получаем сечение индикатрисы - уравнение эллипса.

4. Проводим эллипс к главным осям и находим направления поляризации собственных волн и их показатели преломления.

5. Выбираем схему опыта для измерения электрооптических коэффициентов.

6. По известным табличным значениям r_{i j} рассчитать полуволновые напряжения для измерений r_{i j}.

Теория

Оптические свойства кристаллов в большинстве случаев описываются тензором обратной диэлектрической проницаемости , который в системе собственных осей имеет вид

. (1)

В нецентросимметричных кристаллах возможен линейный электрооптический эффект. Он проявляется в том, что изменения тензора линейно зависят от приложенного поля, т.е.

. (2)

При этом

. (3)

Для наглядного представления оптических свойств кристаллов наиболее часто используется указательная поверхность, называемая оптической индикатрисой. Ее уравнение имеет вид

. (4)

где - радиус-вектор. В декартовой системе координат имеем

. (5)

Оптическая индикатриса представляет собой, в общем случае, трехосный эллипсоид и полностью характеризует оптические свойства прозрачных негиротропных кристаллов.

Большой вклад в теорию электрооптического эффекта внес Поккельс. Далее будем пользоваться его обозначениями.

Будем обозначать , . Тогда изменения компонент (поляризационных констант по Поккельсу)

. (7)

Без влияния внешнего поля

. (8)

После приложения поля

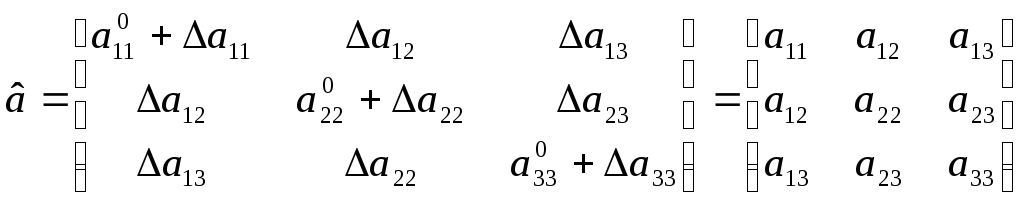. (9)

Оптическая индикатриса при этом принимает вид

(10)

Под действием электрического поля оптическая индикатриса, вообще говоря, поворачивается и деформируется.

Пусть свет в кристалле идет в направлении оси . Сечение оптической индикатрисы плоскостью имеет вид

(11)

и представляет собой эллипс. Путем поворота системы координат на угол , определяемый соотношением

, (12)

эллипс приводится к главным осям и принимает вид

; (13)

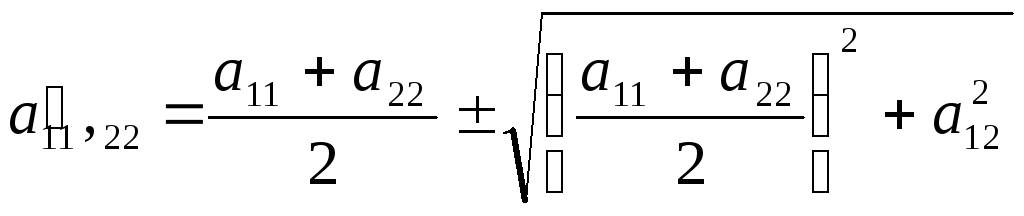. (14)

Длины полуосей эллипса численно равны показателем преломления собственных волн в кристалле, т.е.

(15)

Направления новых осей являются направлениями поляризации собственных волн соответственно.

Аналогичные расчеты проводятся, если свет распространяется в кристалле вдоль оси 0x, 0y или вдоль произвольного направления.

Таким образом, для получения максимального электрооптического эффекта необходимо выбрать направление приложения внешнего электрического поля и направление распространения света . Обычно используется либо продольная геометрия опыта, когда , либо поперечная, когда . Выбор зависит от симметрии кристалла и его физических свойств.

Литература

1. И.С. Желудев Физика кристаллических диэлектриков. М.: Наука, 1968. Гл.20.

2. Переломова Н.В., Тагиева М.М. Задачник по кристаллофизике. М. Наука, 1982. Пр.11.