
Математика курс лекций 1 курс / Лекция 7. Векторы
.docxВекторы. Лекция 7.
Векторы.
Основные понятия.
Величины, которые полностью определяются своим численным значением, называются скалярными. Это площадь, длина, объем, температура, работа, масса и т. д.
Другие величины – сила, скорость, ускорение определяются не только числовым значением, но и направлением. Такие величины называются векторными. Их изображают в виде геометрических объектов – векторов.
Вектор
– направленный
прямолинейный отрезок, т. е. отрезок,
имеющий длину и определенное направление.
Если
 – начало вектора,
– начало вектора,
 – его конец, то такой вектор обозначается
как
– его конец, то такой вектор обозначается
как
 ,
или
,
или
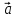 .
Вектор
.
Вектор
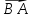 с началом в точке
с началом в точке
 и концом в точке
и концом в точке
 называется противоположным
вектору
называется противоположным
вектору
 и обозначается как
и обозначается как
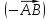 ,
или
,
или
 .
.
Длиной
или модулем вектора
 называется длина отрезка
называется длина отрезка
 и обозначается
и обозначается
 .
.
Вектор,
длина которого равна нулю, называется
нулевым
вектором
и обозначается как
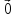 .
Считается, что он не имеет направления.
.
Считается, что он не имеет направления.
Вектор,
длина которого равна 1, называется
единичным
вектором
и обозначается как
 .
.
Векторы
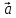 и
и
 называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Это обозначается
как
называются коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Это обозначается
как
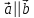 .
Нулевой вектор
.
Нулевой вектор
 считается коллинеарным любому вектору.
считается коллинеарным любому вектору.
Два
вектора считаются равными
 ,
если они одинаково направлены и имеют
одинаковые длины.
,
если они одинаково направлены и имеют
одинаковые длины.
Из
определения равенства векторов следует,
что векторы можно переносить параллельно
своему направлению. Поэтому в дальнейшем
будем считать, что все векторы имеют
начало в точке
 начала координат. Тогда для обозначения
вектора достаточно указать координаты
его конца – точки
начала координат. Тогда для обозначения
вектора достаточно указать координаты
его конца – точки
 .
На рис. 32 изображен вектор
.
На рис. 32 изображен вектор
 ,
на рис. 33 вектор
,
на рис. 33 вектор
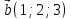 .
.

Три вектора в пространстве называются компланарными, если они лежат в одной или параллельных плоскостях.
Линейные операции над векторами.
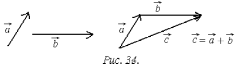
Сложение векторов.
Пусть
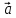 и
и
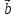 два произвольных вектора. Переместим
вектор
два произвольных вектора. Переместим
вектор
 таким образом, что бы его начало совпало
с концом вектора
таким образом, что бы его начало совпало
с концом вектора
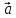 ,
тогда вектор, начало которого совпадает
с началом
,
тогда вектор, начало которого совпадает
с началом
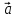 ,
конец – с концом вектора
,
конец – с концом вектора
 ,
называется суммой векторов
,
называется суммой векторов
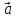 и
и
 и обозначается как
и обозначается как
 (рис. 34). Это правило сложения векторов
называется правилом
треугольника.
Если у векторов
(рис. 34). Это правило сложения векторов
называется правилом
треугольника.
Если у векторов
 и
и
 совместить начала и построить на их
основе параллелограмм, то его диагональ,
проходящая через это начало будет равна
так же вектору
совместить начала и построить на их
основе параллелограмм, то его диагональ,
проходящая через это начало будет равна
так же вектору
 (рис. 35). Это правило называется правилом
параллелограмма.
Разностью векторов
(рис. 35). Это правило называется правилом
параллелограмма.
Разностью векторов
 и
и
 называется сумма векторов
называется сумма векторов
 и
и
 (рис. 36). Таким образом, в параллелограмме,
построенном на векторах
(рис. 36). Таким образом, в параллелограмме,
построенном на векторах
 и
и
 ,
одна диагональ будет равна сумме этих
векторов, другая – их разностью (рис.
37). По свойству сторон и диагоналей
параллелограмма справедлива формула
,
одна диагональ будет равна сумме этих
векторов, другая – их разностью (рис.
37). По свойству сторон и диагоналей
параллелограмма справедлива формула 


 .
.
Произведением
вектора
 на число
на число
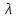 называется вектор
называется вектор
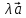 (или
(или
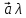 ),
который имеет длину
),
который имеет длину
 ,
коллинеарен вектору
,
коллинеарен вектору
 и имеет то же направление, если
и имеет то же направление, если
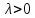 и противоположное вектору
и противоположное вектору
 ,
если
,
если
 .
Таким образом, векторы
.
Таким образом, векторы
 и
и
 всегда коллинеарны.
всегда коллинеарны.
Свойства линейных операций над векторами.
Для
любых векторов
 и
и
 ,
чисел
,
чисел
 и
и
 справедливы следующие соотношения:
справедливы следующие соотношения:
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
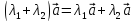 ;
;
5)
 .
.
Обозначим
единичные векторы, направленные вдоль
осей
 и
и
 соответственно через
соответственно через
 и
и
 .
Тогда вектор
.
Тогда вектор
 может быть представлен в виде суммы
векторов
может быть представлен в виде суммы
векторов
 (рис. 38). Соответственно в пространстве
верно равенство
(рис. 38). Соответственно в пространстве
верно равенство
 .
.
Векторы
 называются ортами.
называются ортами.
Длина вектора.
Пусть
вектор
 в трехмерном пространстве имеет
координаты
в трехмерном пространстве имеет
координаты
 .
Тогда его длина равна длине отрезка
.
Тогда его длина равна длине отрезка
 ,
где точки
,
где точки
 и
и
 имеют координаты соответственно
имеют координаты соответственно
 и
и
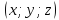 и может быть вычислена по формуле
и может быть вычислена по формуле
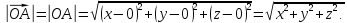
На
плоскости вектор
 имеет длину
имеет длину
 .
.
Условие коллинеарности двух векторов.
Пусть
ненулевые векторы
 и
и
 коллинеарны. Тогда
коллинеарны. Тогда
 ,
следовательно,
,
следовательно,
 .
Отсюда
.
Отсюда
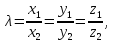 т.
е. координаты векторов пропорциональны.
Это и есть условие
коллинеарности векторов
т.
е. координаты векторов пропорциональны.
Это и есть условие
коллинеарности векторов
 и
и
 .
.
Скалярное произведение векторов.
Скалярным
произведением двух ненулевых векторов
 и
и
 называется число,
равное произведению длин этих векторов
на косинус угла между ними.
называется число,
равное произведению длин этих векторов
на косинус угла между ними.
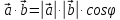 .
.
С
другой стороны скалярное произведение
можно представить как произведение
длины одного вектора на длину проекции
на него второго вектора, как указано,
например, на (рис. 39).
 .
.
Ненулевые
векторы
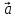 и
и
 назовем ортогональными,
если угол между ними составляет
назовем ортогональными,
если угол между ними составляет
 .
В этом случае
.
В этом случае
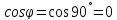 и выполняется равенство
и выполняется равенство
 ,
которое называют условием
ортогональности векторов
,
которое называют условием
ортогональности векторов
 и
и
 .
.
Свойства скалярного произведения векторов.
1)
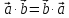 ;
;
2)

3)
 ;
;
4)
 .
.
В
частности, для единичных векторов (орт)
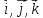 справедливы соотношения
справедливы соотношения
 .
.
Выразим значение скалярного произведения через координаты векторов.
Пусть
в пространстве заданы векторы
 и
и
 .
Тогда
.
Тогда
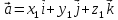 ,
,
 и по свойствам скалярного произведения
и по свойствам скалярного произведения


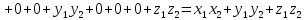 .
.
Таким
образом,
 .
.
Исходя
из этой формулы, можно записать значение
косинуса угла между векторами
 и
и
 в пространстве
в пространстве

Аналогичная
формула верна и для плоских векторов
 и
и
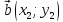
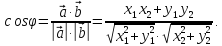
Векторное произведение векторов.
В пространстве рассматриваются векторные произведения векторов.
Векторным
произведением вектора
 на вектор
на вектор
 называется вектор
называется вектор
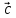 ,
который удовлетворяет следующим трем
свойствам (рис. 40):
,
который удовлетворяет следующим трем
свойствам (рис. 40):
1)
вектор
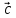 перпендикулярен векторам
перпендикулярен векторам
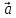 и
и
 ,
т. е.
,
т. е.
 и
и
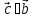 ;
;

2)
вектор
 имеет длину, равную площади параллелограмма,
построенного на векторах
имеет длину, равную площади параллелограмма,
построенного на векторах
 и
и
 ,
т. е.
,
т. е.
 ;
;
3)
вектор
 направлен в ту сторону, из которой
поворот от вектора
направлен в ту сторону, из которой
поворот от вектора
 к вектору
к вектору
 виден против часовой стрелки.
виден против часовой стрелки.
Обозначается
векторное произведение как
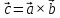 .
.
Свойства векторного произведения.
1)
Для любых векторов
 и
и
 справедливо равенство
справедливо равенство
 ;
;
2)
для любого числа
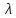 справедливо
справедливо
 ;
;
3)
ненулевые векторы
 и
и
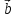 коллинеарны тогда и только тогда, когда
их векторное произведение равно нулевому
вектору
коллинеарны тогда и только тогда, когда
их векторное произведение равно нулевому
вектору
 .
.
4)
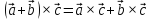 .
.
В
частности, для единичных векторов (орт)
 (рис. 41) справедливы
соотношения
(рис. 41) справедливы
соотношения
 ,
,
 ,
,
 ,
,
 .
.
Выразим
векторное произведение векторов
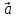 и
и
 через их координаты. Пусть
через их координаты. Пусть
 и
и
 .
Тогда
.
Тогда
 ,
,
 и
по свойствам векторного произведения
и
по свойствам векторного произведения

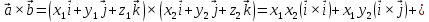

 +
+
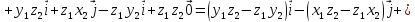

Таким образом

Это есть символическая формула для вычисления координат векторного произведения через координаты исходных векторов.
Так как длина векторного произведения по определению есть площадь параллелограмма, построенного на исходных векторах, то эта площадь вычисляется по формуле
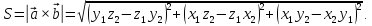
Площадь
треугольника, построенного на векторах
 и
и
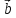 равна
равна
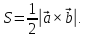
Смешанное произведение векторов.
В пространстве так же можно рассматривать комбинированные векторные и скалярные произведения векторов.
Смешанным
произведением трех векторов
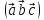 называется скалярное произведение
векторов
называется скалярное произведение
векторов
 и
и
 ,
т. е.
,
т. е.
 .
.
Построим
на векторах
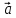 ,
,
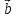 и
и
 параллелепипед (рис. 42). Обозначим
параллелепипед (рис. 42). Обозначим
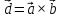 ,
тогда
,
тогда
 .
.
Так
как
 ,
где
,
где
 – площадь параллелограмма, построенного
на векторах
– площадь параллелограмма, построенного
на векторах
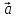 и
и
 ,
а
,
а
 равна
равна
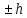 ,
где
,
где
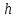 - высота параллелепипеда, то смешанное
произведение равно
- высота параллелепипеда, то смешанное
произведение равно
 ,
где
,
где
 – объем параллелепипеда. Таким образом,
смешанное произведение векторов
– объем параллелепипеда. Таким образом,
смешанное произведение векторов
 ,
,
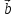 и
и
 по модулю равно объему параллелепипеда,
построенного на этих векторах. Объем
пирамиды, построенных на этих векторах
будет равен
по модулю равно объему параллелепипеда,
построенного на этих векторах. Объем
пирамиды, построенных на этих векторах
будет равен
 .
.
Свойства смешанного произведения.
1)
Смешанное произведение векторов
 ,
,
 и
и
 не меняется при их циклической
перестановке, т. е.
не меняется при их циклической
перестановке, т. е.
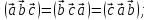
2) смешанное произведение не меняется при перемене местами знаков векторного и скалярного произведений, т. е.
 ;
;
3) смешанное произведение меняет знак при перемене мест любых двух его векторов, т. е.
 ;
;
4)
смешанное произведение ненулевых
векторов
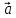 ,
,
 и
и
 равно нулю тогда и только тогда когда
они компланарны.
равно нулю тогда и только тогда когда
они компланарны.
Выразим
значение смешанного произведения
векторов
 ,
,
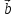 и
и
 через их координаты. Пусть
через их координаты. Пусть
 ,
,
 ,
,
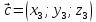 Тогда
Тогда
 ,
,
 ,
,
 и по свойствам векторного и скалярного
произведений, имеем
и по свойствам векторного и скалярного
произведений, имеем
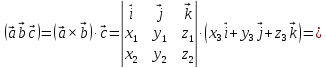

 .
.
Таким образом, справедливо соотношение

