
ВИ_практика_Новое
.pdf
Лабораторная работа №1 Вычисление значений функционала.
Функция y y(x), |
x [a,b] непрерывная вместе со своей первой производной и удовлетво- |
|||||||||||||||||||||||||||||||||
ряющая условию y(a) c, |
y(b) d называется допустимой кривой. |
|
|
|||||||||||||||||||||||||||||||
Обозначим через Y {y C[(1a),b] : y(a) c, y(b) d} |
– множество всех допустимых кривых. Ка- |
|||||||||||||||||||||||||||||||||
ждой |
допустимой |
|
кривой |
y Y |
|
|
|
|
|
поставим |
|
|
|
в |
соответствие |
функционал |
||||||||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
F (x, y, z) C(2) . |
|
|
|
|
|
|
|
||||||||||||||
I ( y) F(x, y(x), yx (x))dx , |
где функция |
Основная задача вариационного ис- |
||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числения(ОЗВИ) имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I ( y) min, |
y Y |
|
|
|
|
|
|
(1) |
|||||||||||||
Допустимая кривая y0 Y |
называется минималью, |
если I ( y0 ) I ( y), y Y . |
|
|
||||||||||||||||||||||||||||||
y0 Y называется слабой минималью и обозначают СМ, если I ( y0 ) I ( y), y Y |
для неко- |
|||||||||||||||||||||||||||||||||
торого 0 . Здесь Y |
-окрестность в пространстве C[(1a),b] кривой y0 : |
|
|
|||||||||||||||||||||||||||||||
Y |
|
|
yx0 (x) yx (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
{y Y : |
y0 (x) y(x) |
, |
, x [a,b]} . |
|
|
|
|
|
|
|||||||||||||||||||||||||
Задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Подобрать значения A и B для условия допустимости кривых y a 1, y b 1 |
|
|||||||||||||||||||||||||||||||||
а) |
y |
Ax B ; б) y |
2 |
Ax 2 Bx C ; в) |
|
y |
3 |
Asin x B ; г) y |
5 |
Ae x B . |
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Вычислить значение фукнционала для полученных фукнций; |
|
|
|
|||||||||||||||||||||||||||||||
3. Сравнить полученные значения и выбрать лучшую функцию для задачи минимизации |
||||||||||||||||||||||||||||||||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y y'2 4 y2 8y cosx 4x2 dx, y 0 1, |
y 2 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
y |
Ax B ; б) y |
2 |
x 2 Ax B ; в) y |
3 |
Asin x B ; г) |
y |
4 |
Ae x |
B . |
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. Подберем значения коэффициентов A и B для заданного условия допустимости кривой |
||||||||||||||||||||||||||||||||||
а) |
y1 |
Ax B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y1 |
0 A 0 B 1 |
|
|
B 1 |
B 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
y |
|
2 A 2 B 2 |
|
A 2 1 2 A 1 2 |
y1 |
|
x 1; |
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) y2 x 2 Ax B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
0 0 A 0 B 1 |
|
|
B 1 |
|
|
|
|
B 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 x2 1.5x 1; |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||
y2 |
2 4 A 2 B 2 |
4 2A 1 |
2 |
|
A |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в) |
y3 Asin x B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y3 0 A 0 B 1 |
|
|
|
B 1 |
|
B 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y3 33.33sin x 1; |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
y3 2 A sin 2 B |
2 |
|
Asin 2 1 |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
y4 Ae x B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
y |
|
0 A 1 B 1 |
|
|
|
A B 1 |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
1 y4 |
0.16e x 0.84; |
|
|
||||||||||||||
|
|
2 A e2 B |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
y |
|
|
|
A e2 1 1 |
|
A |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
|
1 |
||||||||||||||||||||||||||||||||
2. Вычислим значения функционала для полученных допустимых кривых.
а) |
y1 0.5x 1; |
|
y1' 0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
J y |
|
2 |
|
1 |
2 |
|
|
|
x |
|
2 |
|
x |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
5 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 |
|
|
1 |
|
8 |
|
1 cos x |
4x |
|
dx |
|
|
|
4x 5x |
|
|
8cos x 4x cos x dx |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x cos xdx x sin x |
sin xdx x sin x cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
2 |
|
5 |
|
3 |
|
|
|
|
|
|
|
||||
|
u |
x, dv cos xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2x |
|
|
|
x |
|
|
8sin x 4 x sin x cos x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
du dx, v sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
203 |
4 cos 2 16 sin 2 20.95; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
y |
2 |
x2 1.5x 1 , |
y |
2 |
' 2x 1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J y2 |
|
2 |
|
|
|
3 |
2 |
|
|
|
|
2 |
|
3 |
|
|
2 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
2x |
|
|
|
4 x |
|
|
|
|
x |
1 |
8 x |
|
|
|
|
|
x |
1 cos x 4x |
|
dx |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x2 cos xdx x2 sin x 2 x sin xdx x2 sin x 2 x cos x cos xdx x2 2 sin x 2x cos x |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x2 , dv cos xdx |
|
u x, dv sin xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2xdx, v sin x |
|
|
|
du dx, v cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
263 |
20 cos 2 17.09; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
y3 33.33sin x 1 , y3 ' 33.33cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
J y3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4443.56 sin2 x 266.64 sin x 4 8 33.33sin x 1 cosx 4x2 dx |
|
|
|
|
|||||||||||||||||||||||||||||||||
1110.89 cos2 x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6465.01; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) y4 0.16e x |
0.84 , y5 ' 0.16e x |
|
|
|
|
|
|
|||||||
2 |
|
0.16e |
x |
2 |
4 0.16e |
x |
0.84 |
2 |
8 0.16e |
x |
0.84 cos x 4x |
2 |
|
|
J y4 |
|
|
|
|
|
|
|
dx |
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x cos xdx e x sin x e x sin xdx e x sin x e x cos x e x cos xdx |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
e x , dv cos xdx |
u e x , dv sin xdx |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du e x dx, v sin x |
du e x dx, v cos x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
e |
|
cos xdx |
|
|
e |
|
sin x cos x |
|
|
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0.16 2 |
5e |
2x |
8 0.13e x 4 0.84 2 4 0.16e x sin x cos x 8 0.16 sin |
||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравним полученные значения функционала: |
|
|
|||||||||||||||
J |
y1 |
20.95, |
|
|
|
|
|
|
|
|
|||||||
J y2 |
17.09, |
|
|
|
|
|
|
|
|
||||||||
J y3 |
6465.01, |
|
|
|
|
|
|
||||||||||
J y4 |
1527.1 |
|
|
|
|
|
|
|
|
||||||||
Ответ: Лучшая функция для задачи минимизации y2 x 2 |
1.5x 1 . |
||||||||||||||||
|
4 |
|
|
2 |
|
|
|
||||
x |
x3 |
|
1527.1; |
||
|
|||||
|
3 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
2 |
Варианты
|
1 |
y'2 4 y2 8xy 2x2 dx; |
|||
1. |
J y |
||||
|
1 |
|
|
||
|
1 |
y'2 4 y2 2xy x2 dx; |
|||
2. |
J y |
||||
|
1 |
|
|
||
|
1 |
y'2 4 y2 |
4x2 y x cosx dx; |
||
3. |
J y |
||||
|
1 |
|
|
||
|
2 |
y'2 9 y2 |
2xy xsin x dx; |
||
4. |
J y |
||||
|
0 |
|
|
|
|
|
0 |
y'2 4 y2 2 y xe2x dx; |
|||
5. |
J y |
||||
|
2 |
|
|
||
|
1 |
y'2 9 y2 2 y sin x x2ex dx; |
|||
6. |
J y |
||||
|
0 |
|
|
|
|
|
1 |
y'2 4 y2 |
6 yex 2x cosx dx; |
||
7. |
J y |
||||
|
1 |
|
|
||
|
1 |
y'2 y2 4 yex xsin x dx; |
|||
8. |
J y |
||||
|
1 |
|
|
||
|
1 |
y'2 4 y2 8ye2x 3x2 dx; |
|||
9. |
J y |
||||
|
1 |
|
|
||
|
2 |
2 y'2 2 y2 |
y cosx 5x dx; |
||
10. |
J y |
||||
|
0 |
|
|
|
|
|
2 |
2 y'2 2 y2 |
xysin x 6xex dx; |
||
11. |
J y |
||||
|
0 |
|
|
|
|
|
2 |
2 y'2 2 y2 |
y sin2x x2 sin x dx; |
||
12. |
J y |
||||
|
0 |
|
|
|
|
|
2 |
2 y'2 2 y2 |
y cosx xe2x dx; |
||
13. |
J y |
||||
|
0 |
|
|
|
|
|
2 |
2 y'2 2 y2 |
ye2x sin3x x sin x dx; |
||
14. |
J y |
||||
|
1 |
|
|
|
|
|
1 |
2 y'2 2 y2 |
yex 4xe2x dx; |
||
15. |
J y |
||||
|
1 |
|
|
||
|
|
1 |
|
|
|
|
|
16. |
J y 2 y'2 2 y2 3yex cosx 5x2e2x dx; |
||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
2 ye2x 4sin x dx; |
||||
17. |
J y 2 y'2 2 y |
||||||
|
|
1 |
|
|
|
|
|
|
|
4 |
y'2 4 y2 |
4 y cos2x 3x2 dx; |
|||
18. |
J y |
||||||
|
|
2 |
|
|
|
|
|
|
|
1 |
y'2 9 y2 |
6 y sin3x 5x2 dx; |
|||
19. |
J y |
||||||
|
|
0 |
|
|
|
|
|
|
|
2 |
y'2 4 y2 |
4 yex sin x x2 sin x dx; |
|||
20. |
J y |
||||||
|
|
0 |
|
|
|
|
|
|
|
2 |
y'2 4 y2 |
4 yex sin2x x2 dx; |
|||
21. |
J y |
||||||
|
|
0 |
|
4 ye x x sin x dx; |
|||
|
|
1 |
|||||
22. |
J y |
y'2 y 2 |
|||||
|
|
1 |
|
|
|
|
|
|
J y |
2 |
y'2 9 y 2 |
2xy x sin x dx; |
|||
23. |
|
||||||
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
24. |
J y |
2 y'2 2 y 2 ye 2x 4 sin x dx; |
|||||
|
|
1 |
|
|
|
|
|
|
|
2 |
y'2 4 y2 |
8y cosx 4x2 dx; |
|||
25. |
J y |
||||||
|
|
0 |
|
|
|
|
|
|
|
4 |
y'2 4 y2 |
4 y cos2x 3x2 dx; |
|||
26. |
J y |
||||||
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
27. |
J y y'2 2 y'ex sin x ex cosx dx; |
|
|||||
|
|
1 |
|
|
|
|
|
|
|
1 |
y'2 9 y2 |
4 ye2x cos3x dx; |
|
|
|
28. |
J y |
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
0 |
4 y sin3x 5x2 dx; |
|
|||
29. |
J y y'2 9 y2 |
|
|||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
30. |
J y y'2 2 y'ex cosx dx; |
|
|||||
|
|
1 |
|
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
3 |

Лабораторная работа №2 Построение экстремалей для функционалов.
Пусть дана некоторая допустимая кривая y(x) Y , тогда функция y x , x a,b назы-
вается вариацией этой допустимой кривой, если y(x) y(x) y(x), x [a,b] снова является допустимой, то есть y(x) Y .
Удобно вариацию представлять в виде: y(x) h(x), x [a,b] , где h(x) – описывает форму вариации, а множитель еѐ величину. При 1, y h , поэтому функцию h(x) также называют вариацией допустимой кривой.
Из определения допустимых кривых вытекает, что некоторая функция h(x), x [a,b]
будет вариацией тогда и только тогда, когда |
|
|||
1) |
h(x) C(1) |
; |
|
|
|
[a,b] |
|
|
|
2) |
h(a) h(b) 0 . |
|
|
|
Обозначим через H h x C(1) |
: h a h b 0 . Для ОЗВИнекоторая вариация |
h H |
||
|
|
[a,b] |
|
|
подходит сразу для всех допустимых кривых.
Вариация |
h0 {h(x) 0, x [a,b]} |
называется тривиальной: она оставляет любую до- |
||||||||||||||||||||||||||||||||||
пустимую кривую на месте. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Зафиксируем некоторую допустимую кривую |
y Y |
|
и вариацию h H , тогда если до- |
|||||||||||||||||||||||||||||||||
пустимо разложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Y ( y) Y ( y) Y ( y) Y ( y h) Y ( y) Y ( y, h) |
|
|
|
(2) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
2Y ( y, h) 0( 2 ) , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
то коэффициент при называетсяпервой вариацией функционала, а коэффициент при |
2 |
|||||||||||||||||||||||||||||||||||
– |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
второй вариацией функционала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Из разложения (2) следуют правила вычисления вариаций функционала: |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
, 2 J y, h |
d 2 |
|
J y h |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
J y, h |
|
|
J y h |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
d |
|
|
d 2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для функционала J y ОЗВИ получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
d b |
|
|
|
|
|
|
|
|
|
|
b |
F x, y, y |
|
|
|
|
|
F |
x, y, y |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
J y, h |
|
|
|
F x, y h, yx hx dx |
|
|
|
|
|
|
|
|
x |
|
h x |
|
|
|
|
|
x |
|
|
(2а) |
||||||||||||
d |
|
|
|
|
|
y |
|
|
|
|
|
|
yx |
|
|
hx x dx , |
||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
0 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
d |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 J y, h |
|
F x, y h, yx hx |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
d 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2б) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
b |
2 |
F x, y, yx h2 x 2 |
2 |
F x, y, yx h x hx x |
2 |
F x, y, yx hx2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
x dx |
|
|
|
|
|||||||||||||||||||||||||||
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
y yx |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
||||||
Теорема 1 Пусть y 0 – слабая минималь ОЗВИ, тогда:
1)Y ( y0 , h) 0, h H (условие стационарности);
2)2Y ( y0 , h) 0, h H .
Теорема 2(условие Эйлера). Если y 0 – слабая минималь ОЗВИ, то она необходимо всюду на [a,b] должна удовлетворять уравнению
F |
|
d |
|
F |
0 (уравнение Эйлера) |
(3) |
|
|
|
||||
y |
|
dx yx |
|
|||
(т.е. при подстановке в уравнение (3) y0 должна обращать его в верное тождество на [a,b]).
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
4 |
Из теоремы 2 следует, что решение ОЗВИ надо искать только среди решений уравнения (3).
Распишем подробно уравнение (3) вычислив во 2-м слагаемом полную производную по x (для удобства умножим уравнение (3) на -1):
2 F |
y xx |
2 F |
y x |
2 F |
|
F |
0 |
* |
|
|
|
|
(3 ) |
||||
2 |
y y x |
x y x |
y |
|||||
y x |
|
|
|
|
|
Из (3*) видно, что относительно искомой функции y уравнение Эйлера, есть обыкно-
венное дифференциальное уравнение II-го порядка. Предположим, что мы нашли его общее решение на [a, b]:
y (x,c1,c2 ), x a,b
Выделим из него допустимые кривые. Они выделяются с помощью условий y (a, c1, c2 ) c .
y (b, c1, c2 ) d
Допустимые кривые, которые являются решением уравнения Эйлера называются
экстремалями ОЗВИ.
Условие Эйлера можно переформулировать: любая слабая минималь находится среди экстремалей задачи.
Для решения ОЗВИ надо: по функционалу построить уравнение Эйлера, решить его, построить экстремали и проверить условия существования решения и условия II-го порядка.
Задание. Для каждого фукнционала:
1.Составить развернутое уравнение Эйлера;
2.Найти общее решение уравнения;
3.Построить экстремаль;
4.Для первого функционала вычислить значение на экстремали;
5.Построить график экстремали (по возможности).
Пример
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx, y 0 1, y 2 1 |
|
|
||||||||||
|
J y y'2 4 y2 |
8y cosx 4x2 |
|
|
||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. Составляем развернутое уравнение Эйлера: |
|
|
|
|||||||||||||||||||||||||
|
F x, y, y |
x |
|
y'2 4 y 2 8 y cos x 4x2 ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
8y |
8cos x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
F |
|
|
|
|
|
2 F |
|
|
|
2 F |
|
|
|
2 F |
|
|
|
d F |
|
|
|
||||||
|
|
|
2 y' |
|
|
|
|
|
2 , |
|
|
|
0 , |
|
|
|
|
0 , |
|
|
|
2 y'' |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
yx |
|
, 2 yx |
|
|
y yx |
|
|
|
x yx |
|
|
|
; |
|
|||||||||||||
|
|
|
|
|
|
|
|
dx yx |
|
|
||||||||||||||||||
2y'' 0 y' 0 8y 8cos x 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y'' 4y 4cos x – развернутое уравнение Эйлера. |
|
|
|||||||||||||||||||||||||
2. Находим общее решение уравнения: |
|
|
|
|||||||||||||||||||||||||
|
y y0 y1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a) 2 4 0; |
|
|
2; |
y |
0 |
C e2x |
C |
2 |
e 2x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 Asin x B cos x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
y1' Acos x B sin x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
y1'' Asin x B cos x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
5 |
|||||||||||||||||||||||||||
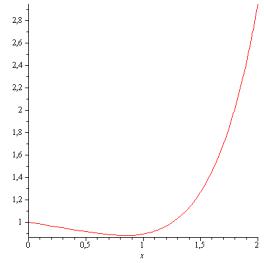
Asin x B cos x 4Asin x 4B cos x 4D 4cos x; |
|
|
|
|
|
|||||||||||||||||||||||||||||||
A 0, |
B |
4 |
, D 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y C e2x C |
|
e 2x |
|
4 |
cos x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Находим экстремаль: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y 0 C e2 0 |
C |
|
e 2 0 |
|
4 |
cos0 C C |
|
|
4 |
1; |
|
C C |
|
|
1 |
|
||||||||||||||||||||
2 |
|
2 |
|
|
2 |
|
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
1 |
|
5 |
|
|
1 |
|
5 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y 2 C e4 C |
|
e 4 |
|
|
4 |
|
|
|
|
|
C e8 C |
|
|
|
|
|
4 |
|
|
|
e4 |
|||||||||||||||
2 |
|
|
|
|
cos 2 1; |
2 |
1 |
|
|
|
cos 2 |
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
C |
5 4cos 2 e4 1 |
0.024; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
5 e8 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
C2 0.176; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y 0.024e2x 0.176e 2x |
4 |
cosx – экстремаль. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Вычисляем значение на экстремали: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx 9.898 |
|
|
|
|
|
|
|
|
|
|
|
||||
J y |
y'2 4 y 2 8 y cos x 4x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
0
Значение функционала на лучшей функции из лабораторной работы №1 J y1 11.392 больше значения на полученной экстремали J y 9.898 .
5. График экстремали имеет вид:
Варианты |
|
|
|
|
|
|
|
|
Вариант 1 |
|
|
|
Вариант 2 |
|
|
|
|
1 |
|
dx; y 1 3, y 1 1; |
1 |
dx; y 1 2, y 1 4; |
||||
J y y'2 4 y 2 8xy 2x2 |
J y y'2 4 y2 2xy x2 |
|||||||
1 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
2 |
y'2 4 y'sin 2x x2 dx; |
|
|
|
J y y'2 4 y'e2x sin 2 x dx; |
y 0 1, y 2 2; |
J y |
y 0 1, y 2 1; |
|||||
0 |
|
|
|
0 |
|
|
|
|
5 |
|
|
|
2 |
y'2 4 y2 8y cos x 4x2 dx; |
|
||
J y yy'2 dx; |
y 1 2, y 5 6; |
|
J y |
y 0 1, y 2 3; |
||||
1 |
|
|
|
0 |
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
6 |
Вариант 3 |
|
|
Вариант 8 |
|
|
||
1 |
4x2 y x cos x dx; y 1 2, y 1 0.5; |
1 |
4 ye x x sin x dx; |
|
|||
J y y'2 4 y2 |
J y y'2 y2 |
y 1 1, y 1 3; |
|||||
1 |
|
|
1 |
|
|
||
2 |
y'2 4 y'cos 2x 5sin 3x dx; |
|
4 |
y'2 4 y 2 |
4 y cos 2x 3x2 dx; y 2 1, y 4 4; |
||
J y |
y 0 2, y 2 3; |
J y |
|||||
0 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
|
|
|
J y yy'2 dx; y 0 2, y 1 1; |
|
J y yy'2 dx; y 1 2, y 3 5; |
|
||||
0 |
|
|
|
1 |
|
|
|
Вариант 4 |
|
|
Вариант 9 |
|
|
||
2 |
y'2 9 y2 |
2xy x sin x dx; |
|
1 |
|
|
|
J y |
y 0 1, y 2 2; |
J y y'2 4 y2 8 ye2x 3x2 dx; |
y 1 1, y 1 3; |
||||
0 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
J y yy'2 dx; y 0 2, y 1 1; |
|
J y y' y'2 cos 2 x sin 2 x dx; y 1 1, y 1 2; |
|||||
0 |
|
|
|
1 |
|
|
|
0 |
4 y sin 3x 5x2 dx; y 1 2, y 0 0; |
5 |
|
|
|
||
J y y'2 9 y2 |
J y yy'2 dx; y 1 2, y 5 6; |
|
|||||
1 |
|
|
1 |
|
|
|
|
Вариант 5 |
|
|
Вариант 10 |
|
|
||
0 |
2 y xe2x dx; y 2 0, y 0 1; |
2 |
2 y'2 2 y2 y cos x 5x dx; |
|
|||
J y y'2 4 y2 |
J y |
y 0 2, y 2 2; |
|||||
2 |
|
|
0 |
|
|
|
|
1 |
|
|
3 |
y' y'2 sin 2 x e2x dx; y 1 1, y 3 4; |
|||
J y y'2 2 y'e x cos x dx; y 1 2, y 1 3; |
J y |
||||||
1 |
|
|
1 |
|
|
|
|
5 |
|
|
|
3 |
|
|
|
J y yy'2 dx; y 2 3, y 5 6; |
|
J y yy'2 dx; y 1 2, y 3 5; |
|
||||
2 |
|
|
|
1 |
|
|
|
Вариант 6 |
|
|
Вариант 11 |
|
|
||
1 |
y'2 9 y2 |
2 y sin x x2e x dx; y 0 1, y 1 1; |
2 |
2 y'2 2 y2 xy sin x 6xe x dx; y 0 1, y 2 2; |
|||
J y |
J y |
||||||
0 |
|
|
|
0 |
|
|
|
1 |
y'2 9 y2 |
4 ye 2x cos 3x dx; |
|
2 |
y' y'2 e x sin x dx; y 0 2, y 2 1; |
||
J y |
y 0 3, y 1 2; |
J y |
|||||
0 |
|
|
|
0 |
|
|
|
5 |
|
|
|
4 |
|
|
|
J y yy'2 dx; y 1 2, y 5 6; |
|
J y yy'2 dx; y 0 2, y 4 4; |
|
||||
1 |
|
|
|
0 |
|
|
|
Вариант 7 |
|
|
Вариант 12 |
|
|
||
1 |
6 ye x 2x cos x dx; y 1 1, y 1 3; |
2 |
2 y'2 2 y2 y sin 2x x2 sin x dx; y 0 1, y 2 4; |
||||
J y y'2 4 y 2 |
J y |
||||||
1 |
|
|
0 |
|
|
|
|
1 |
|
|
1.5 |
|
|
||
J y y'2 4 y'e x cos x sin x dx; |
y 1 1, y 1 2; |
J y y' y'2 sin 2x cos 2x dx; y 0.5 1, y 1.5 2; |
|||||
1 |
|
|
0.5 |
|
|
||
2 |
|
|
|
3 |
|
|
|
J y yy'2 dx; y 0 1, y 2 3; |
|
J y yy'2 dx; y 1 2, y 3 5; |
|
||||
0 |
|
|
|
1 |
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
7 |
Вариант 13 |
|
Вариант 18 |
|
|
2 |
2 y'2 2 y2 y cos x xe2x dx; |
|
4 |
4 y cos 2x 3x2 dx; y 2 2, y 4 3; |
J y |
y 0 1, y 2 2; |
J y y'2 4 y2 |
||
0 |
|
|
2 |
|
2 |
y' xy'2 x2 y' dx; y 1 2, y 2 1; |
1 |
2x 2xy' dx; y 1 2, y 1 1; |
|
J y |
J y y' y'2 e |
|||
1 |
|
|
1 |
|
|
|
2 |
J y yy'2 dx; y 0 1, y 2 3; |
||
|
|
0 |
Вариант 14 |
||
|
|
2 |
J y |
|
2 y'2 2 y 2 ye 2x sin 3x x sin x dx; |
|
|
1 |
y 1 2, y 2 3; |
||
|
|
1 |
J y |
|
y' e x y'2 xy' dx; y 1 0, y 3 2; |
|
|
1 |
|
|
5 |
J y |
|
yy'2 dx; y 2 3, y 5 6; |
|
|
0 |
Вариант 15 |
||
|
|
1 |
J y |
2 y'2 2 y 2 ye x 4xe 2x dx; y 1 1, y 1 2; |
|
|
|
1 |
|
|
2 |
J y |
y'2 4 y 2 8 y cos x 4x2 dx; y 0 1, y 2 3; |
|
|
|
0 |
|
|
3 |
J y |
yy'2 dx; y 1 2, y 3 5; |
|
|
|
1 |
Вариант 16 |
||
|
|
1 |
J y |
|
2 y'2 2 y 2 3ye x cos x 5x2e2x dx; |
|
|
1 |
y 1 2, y 1 1; |
||
|
|
2 |
J y |
|
y' y'2 x2 y'2 dx; y 0 1, y 2 2; |
|
|
0 |
|
3 |
|
|
J y yy'2 dx; y 1 2, y 3 5; |
|
||
|
1 |
|
|
Вариант 19 |
|
|
|
|
1 |
6 y sin 3x 5x2 dx; |
|
J y y'2 9 y2 |
y 0 3, y 1 1; |
||
|
0 |
|
|
|
1 |
|
|
J y y' y'2 e x xy' dx; y 1 0, y 3 2; |
|||
|
1 |
|
|
|
5 |
|
|
J y yy'2 dx; y 2 3, y 5 6; |
|
||
|
2 |
|
|
Вариант 20 |
4 ye x sin x x 2 sin x dx; |
||
|
2 |
||
J y |
y'2 4 y 2 |
||
|
0 |
|
|
y 0 2, y 2 3; |
|
|
|
|
1 |
|
|
J y |
y'2 2 y' e x sin x e x cos x dx; |
y 1 2, y 1 3; |
|
|
1 |
|
|
|
4 |
|
|
J y |
yy'2 dx; y 0 2, y 4 4; |
|
|
|
0 |
|
|
Вариант 21 |
|
|
|
|
2 |
4 ye x sin 2x x2 dx; y 0 2, y 2 3; |
|
J y y'2 4 y2 |
|||
|
0 |
|
|
1 |
y' e x y'2 xy' dx; y 1 0, y 3 2; |
J y |
1
5 |
|
|
|
4 |
|
|
J y yy'2 dx; y 1 2, y 5 6; |
|
|
J y |
yy'2 dx; y 0 2, y 4 4; |
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Вариант 17 |
|
|
Вариант 22 |
|
|
|
|
|
|
|
|
||
1 |
|
|
|
1 |
|
|
J y 2 y'2 2 y2 ye2x 4sin x dx; |
|
|
|
|
||
y 1 4, y 1 3; |
J y |
y'2 y2 4 ye x xsin x dx; |
y 1 1, y 1 3; |
|||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
2 |
|
|
J y y' y'2 cos 2x sin 2x dx; |
y 0.5 1, y 0.5 0.5;J y |
|
|
|||
y'2 4 y'e2x sin 2 x dx; |
y 0 1, y 2 2; |
|||||
0.5 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
1 |
|
|
J y yy'2 dx; y 0 2, y 4 4; |
|
|
|
|
|
|
|
|
J y |
yy'2 dx; y 0 2, y 1 1; |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
8 |
Вариант 23 |
|
|
|
|
|
|
|
|
|
|
Вариант 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
y'2 9 y2 2xy x sin x dx; |
|
|
2 |
y'2 4 y2 |
|
4 ye x sin 2x x2 dx; |
|
|||||||||||||||||||||||||||||||
J y |
y 0 1, y 2 2; |
J y |
|
y 0 2, y 2 3; |
||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y' |
2 |
|
|
|
|
x |
cos x sin x dx; |
y 1 1, y 1 2; |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||||||||
|
4 y'e |
|
|
x |
2 |
1y' |
2 |
y' e |
|
|
||||||||||||||||||||||||||||||
J y |
|
|
|
J y |
|
|
|
|
|
|
dx; y 2 1, y 4 2; |
|||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y yy'2 dx; y 1 2, y 5 6; |
|
|
|
1 y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
J y |
|
|
|
dx; y 1 4, y 5 2; |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 24 |
|
|
|
|
|
|
|
|
|
|
Вариант 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
J y 2 y'2 2 y2 |
|
ye 2x 4sin x dx; y 1 4, y 1 3; |
|
|
|
|
|
|
|
|
|
|
|
|
4 y sin 3x 5x2 dx; |
y 1 2, y 0 0; |
||||||||||||||||||||||||
|
J y y'2 9 y2 |
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y y' xy'2 x2 y' dx; |
y 1 2, y 2 1; |
|
y'2 2xy'ln x ln x dx; y 1 1, y 3 2; |
|||||||||||||||||||||||||||||||||||||
J y |
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y yy'2 dx; y 0 2, y 4 4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
J y y |
|
y' |
dx; y 1 1, y 5 7; |
|
|||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 25 |
|
|
|
|
|
|
|
|
|
|
Вариант 29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y y'2 4 y2 8 y cos x 4x2 dx; y 0 1, y 2 3; |
|
y'2 9 y2 |
|
4 ye2x cos 3x dx; y 0 3, y 1 2; |
||||||||||||||||||||||||||||||||||||
J y |
|
|||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
2 y' |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
J y |
|
y'2 |
|
|
|
|
|
|
|
|
e3x dx; y 2 1, y 4 2; |
J y y' |
2 |
2 y'e |
x |
sin x e |
x |
cos x dx; y 1 2, y 1 3; |
||||||||||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J y y 1 y'2 dx; y 1 3, y 5 6; |
|
|
|
y 1 y'2 dx; y 1 6, y 5 1; |
|
|||||||||||||||||||||||||||||||||||
J y |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 26 |
|
|
|
|
|
|
|
|
|
|
Вариант 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y y'2 4 y 2 4 y cos 2x 3x2 dx; y 2 1, y 4 4; |
|
y'2 4 y2 |
|
8 y cos x 4x2 dx; y 0 1, y 2 3; |
||||||||||||||||||||||||||||||||||||
J y |
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
4 |
|
|
|
4 y' |
|
|
|
y 2.5 2, y 4 4; |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
||||||||||
|
y'2 |
|
|
|
|
|
|
|
sin 2x dx; |
|
|
|
2 |
|
|
|
2 y' |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
J y |
|
y' |
|
|
|
|
|
|
|
|
|
|
|
e |
|
dx; y 2 2, y 4 2; |
|||||||||
|
2.5 |
|
|
|
4 x |
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y yy'2 dx; y 1 2, y 5 6; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
J y y 1 y'2 dx; y 2 4, y 5 6. |
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
9 |

Лабораторная работа №3 Задачас функционалом от нескольких функций.
Условие Эйлера будет справедливо и для случая функционалов, зависящих от нескольких функций.
ТеоремаВ случае, если фукнционал зависит от нескольких фукнций
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ( y) F(x, y1,..., yn , y1',..., yn ')dx , удовлетворяющих условиям yi a ci , yi b di i |
|
, необ- |
||||||||||||
1, n |
||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ходимыми условиями экстремума будут условия |
||||||||||||||
F |
|
|
|
d F |
0, |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
y |
|
dx |
y ' |
|||||||||||
|
1 |
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
||||
|
F |
|
|
|
d F |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0. |
||
y |
|
|
|
dx y |
|
|
||||||||
|
n |
|
|
|
n |
' |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задание:
1.Составить систему уравнений Эйлера;
2.Найти общее решение системы;
3.Построить экстремаль;
4.Вычислить значение фукнционала.
Пример
|
|
2 |
2 y' z' y2 z 2 ze2x dx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
J y, z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y 2 0, z 2 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y 2 3, |
z 2 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. Составим систему уравнений Эйлера: |
|
|
|
|
|
|
|
|||||||||||||||||||||
F |
|
d |
|
F |
0 |
F |
2 y, |
F |
2z', |
|
d |
|
F |
2z' ' |
|
|||||||||||||
|
y |
|
dx yx |
|
|
y |
|
y x |
|
|
|
|
|
dx y x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
' |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
|
d F |
0 |
|
F |
2z e |
2x |
, |
F |
2 y', |
d F |
2 y' |
|||||||||||||||
|
z |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dx |
|
x |
z |
|
z |
x |
|
dx z |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2z'' 2 y 0
2x
2 y'' 2z e
2. Находим общее решение системы дифференциальных уравнений:
yz'' y'' z(4) ;
z(4) z 12 e2x z z0 z1
4 1 0 2 1 |
1, |
|
|
i |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
3,4 |
|
|
|
|
|
|
||
z |
0 |
C e x |
C |
2 |
e x C |
3 |
sin x C |
4 |
cos x |
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
z Ae |
2x |
z |
(4) |
16 Ae |
2x |
|
1 |
e |
2x |
, A |
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
32 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
1 |
e2x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z C e x C |
|
e |
x C |
|
sin x C |
|
cos x |
1 |
e2x ; |
|
|||||||||||||||||
2 |
3 |
4 |
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариационное исчисление. Практика Мережа В.Л., Ратобыльская Д.В. |
10 |
||||||||||||||||||||||||||
