
Termeh_shpory
.docx
![]() где
где ![]() и
и ![]() -
масса и расстояние от оси вращения
-
масса и расстояние от оси вращения ![]() частицы
частицы
твердого тела , ![]() -
его угловая скорость. Обозначив вел,
стоящую в круглых скобках, через I,
получим
-
его угловая скорость. Обозначив вел,
стоящую в круглых скобках, через I,
получим![]()
где I - так наз момент инерции твер тела относит оси00':

48.

𝜔
– угловая скорость,
 -
расстояние до точки, кот в данный момент
вращается
-
расстояние до точки, кот в данный момент
вращается

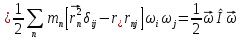 ;
;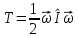
35,36
Будем
рассматривать р-е ур-ий дв-я кол-ся
мех-ой сис-мы в лин прибл.,т.е когда будем
строить ф-ю Лагранджа,то ф-ии будет
реализовывать разложение слагаемых
до 2ого порядка по оклон.обобщающих
координ.от состояния устойчивого
равновесия. L(ϕ,ψ,ϕ,ψ)Пусть
механич.сис-ма имеет r
степеней свободы.Эта механич.сис ма
определ-ся обобщ.коорд. коорд-ми
q1,q2….qr..Обозначим
qr,где
L=1,2….r,тогда
L=L(qλ,qλ)=T-U(qλ)Будем
рассматривать состо-я мех сис-мы,где
потенц.энергия минимальна.Xλ=qλ-q(0)λ
отклон.обобщ.коорд-ты
от положения
равновесия. U(qλ)=U(q(0)λ+xλ)=
U(q(0)λ)+ +
+
 +…. T=
+…. T= Ф-ю Лагранжа для колеб.многомерной
сис-мы в лин.приближении можем записать
в виде L=
Ф-ю Лагранжа для колеб.многомерной
сис-мы в лин.приближении можем записать
в виде L= где
где
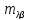 координаты опред.пар-ми
координаты опред.пар-ми
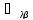 коэ-ты
коэ-ты![]()
57.L
TL=LL
T=I-усл
ортогональности.Матр L
облад св-ми ортогон наз матр Лор.
x'=Lxx
(1);x’=Lx(1’)-
преобр Лор.Из опр этой матр след частн
преобр Лор.
 x1’=L11x1+L14x4;x2’=x2;x3’=x3;x4’=L41x1+L44x4;
L112+L412=1
x1’=L11x1+L14x4;x2’=x2;x3’=x3;x4’=L41x1+L44x4;
L112+L412=1
L11L14+L41L44=0 ; L142+L442=1
x'=L11x+L14x4;L11x+L14ict=0(3);L14/L11=-i
L11=1/1-2 ; L44=1/1-2 ;L14=i/1-2 ;L41= -i/1-2
(1/1-2)+(2/1-2)=(1/1-2)-док-ли L11
x1’=(x/1-2)+(x4i/1-2);x4’=(-ix/1-2)+(x4/1-2);x’=(x-t)/1-2;ict’=(i(/c2)x+ict)/1-2 t’=(t-(/c2)x)/1-2; =/c;
L= 1/1-2 0 0 i/1-2 0 1 0 0 -i/1-2 0 0 1/1-2 0 0 1 0
x’=(x-t)/1-2; y=y’ z=z’ -частные преобра Лоренца
t’=t-(/c2)x/1-2
<<cx=x’-t;y’=y;z’=z;t’=t(обычные преобразования Галилея).
50
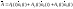
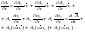
 ,
, -относительная
(локальная) производная. Производная
вектора А связана с переносным
вращательным движением.
-относительная
(локальная) производная. Производная
вектора А связана с переносным
вращательным движением.
55.Ориентация вращ-ия ТВ.тела опр-ся углами Эйлера:
 -прецесионный
угол, θ
-нутационный,
-прецесионный
угол, θ
-нутационный,
ψ -угол собств.вращения ТВ.тела.
В мех-ке вращ.тв.тела эти 3 угла явл.обобщ.коорд.и
Они
явл.3 степ. свободы ТВ.тела.
X=L-ось
Lили
ось узлов Нутационное вращение со
временем мен-ся(θ);
I1=I2=I3;L=T-U= =L(
=L( θ
, ψ,
θ
, ψ, θ
, ψ);
θ
, ψ);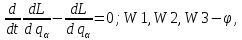 θ
, ψ;
θ
, ψ;
W=W1n1+W2n2+W3n3=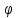 n3+ θ n3+ ψ n3;W3= ψ+
n3+ θ n3+ ψ n3;W3= ψ+ θ;
θ;
N3=an3+bn3;n1=an2+bn1;a=sin ψ;
B=cos
ψ;W1= sin ψ sin θ+ θ cos ψ;
sin ψ sin θ+ θ cos ψ;
W2=
 cos ψ sin θ- θ sin ψ
cos ψ sin θ- θ sin ψ
56Дифференциальное
уравнения вращательного движения
твердого тела может быть получено,
исходя из теоремы об изменении
кинетического момента
![]()

![]() это кинети момент
тела относительно оси вращения.принимая
это кинети момент
тела относительно оси вращения.принимая
![]() получим
получим![]() или
через угол вращения
или
через угол вращения![]() .
(1) это есть уравнение вращательного
движения(в диф.форме) твердого тела.
Используя уравнение (1)можно решать
следующие две основные задачи динамики
вращательного движения твердого тела:
.
(1) это есть уравнение вращательного
движения(в диф.форме) твердого тела.
Используя уравнение (1)можно решать
следующие две основные задачи динамики
вращательного движения твердого тела:
1) Зная вращательный момент, найти закон вращения тела или его угловую скорость w , т.е. j =f(t).
2) Зная закон вращения, т.е. j =f(t), найти вращательный момент внешних сил.
Частный случай:
Если![]() то тело вращается равноускоренно, т.е.
e =const.
то тело вращается равноускоренно, т.е.
e =const.
19.z1=0,
z2=0
– ур-ия связи y1=0,
y2=0
x1+x2+ =0
– длина нерастяжимой нити. Эта система
имеет одну степень свободы. Используем
общее ур-ие динамики:
=0
– длина нерастяжимой нити. Эта система
имеет одну степень свободы. Используем
общее ур-ие динамики:
 +
+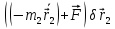 =0;
=0;
 +
+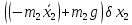 =0,
поскольку
=0,
поскольку
 ,
тогда получаем:
,
тогда получаем:
 =0,
тогда
=0,
тогда
 ,
поскольку из
,
поскольку из
 ,
то
,
то
 .
.
11.
Будем рассматривать движение маятника
при условии, что угол отклонения мал,
тогда, если измерять угол в радианах,
справедливо утверждение: На тело
действуют сила тяжести и сила натяжения
нити. Равнодействующая этих сил имеет
две составляющие: тангенциальную,
меняющую ускорение по величине, и
нормальную, меняющую ускорение по
направлению (центростремительное
ускорение, тело движется по дуге).Т.к.
угол мал, то тангенциальная составляющая
равна проекции силы тяжести на касательную
к траектории:![]() Угол
в радианах равен отношению длины дуги
к радиусу (длине нити), а длина дуги
приблизительно равна смещению (x »s):
Угол
в радианах равен отношению длины дуги
к радиусу (длине нити), а длина дуги
приблизительно равна смещению (x »s):
![]() Сравним полученное уравнение с уравнением
колебательного движени
Сравним полученное уравнение с уравнением
колебательного движени
![]()

![]()
![]()
![]() Аналогичные
вычисления можно проделать с помощью
закона сохранения энергии. Учтем, что
потенциальная энергия тела в поле
тяготения равна
Аналогичные
вычисления можно проделать с помощью
закона сохранения энергии. Учтем, что
потенциальная энергия тела в поле
тяготения равна
![]()
![]() а
полная механическая энергия равна
максимальной потенциальной или
кинетической:
а
полная механическая энергия равна
максимальной потенциальной или
кинетической:
![]() Запишем закон сохранения энергии и
возьмем производную от левой и правой
частей уравнения:
Запишем закон сохранения энергии и
возьмем производную от левой и правой
частей уравнения:
![]() Т.к. производная от постоянной величины
равна нулю, то
Т.к. производная от постоянной величины
равна нулю, то
![]() Производная суммы равна сумме производных:
Производная суммы равна сумме производных:
![]()

![]()
Следовательно
![]()
![]()
20.Н.У.
 ,
,
 ,
m
,
m =(0,-mg),
=(0,-mg),
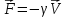 =(-
=(- ,
-
,
- )=
(-
)=
(-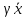 ,
-
,
-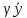 );
);
m =
m
=
m ;
;
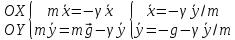 ;
Пусть
;
Пусть
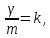
 ;
; ;
;
 =0;
=0;
 =0;
=0;
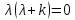 ;
;
 ;
;
 ;
x=C1e0t+
C2e-kt=
C1+
C2-kt;
t=0;
0= C1+
C2;
C1=
-C2;
;
x=C1e0t+
C2e-kt=
C1+
C2-kt;
t=0;
0= C1+
C2;
C1=
-C2;
 =-
C1e-kt
=-
C1e-kt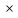 (-k)=
C1ke-kt
(-k)=
C1ke-kt
C1=V0cosα/k;

 =-g;
y=y0+
=-g;
y=y0+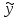 ;
;
 =0;
=0;
 =0;
x1=0;
=0;
x1=0;
 y0=
C3+
C4-kt;
t=0; C3+
C4=0;
C3=-
C4;
y0=
C3(1-e-kt);
y0=
C3+
C4-kt;
t=0; C3+
C4=0;
C3=-
C4;
y0=
C3(1-e-kt);
 ;
t=0; V0sinα=
;
t=0; V0sinα=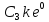 ;
;
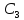 =
V0sinα/k;
y0=
V0sinα(
=
V0sinα/k;
y0=
V0sinα( )/k;
)/k;

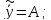
 kA=-g; A=-g/k;
kA=-g; A=-g/k;
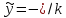 ;
;
 –кинем-ий з-н
–кинем-ий з-н
hmax
если
 t,
t,
 =0;
V0sinα
=0;
V0sinα =g/k;
=g/k;
 g/k
V0sinα;
t=-ln(g/k
V0sinα)/k;
l=
V0cosα/k-
gcosα/k2sinα;
g/k
V0sinα;
t=-ln(g/k
V0sinα)/k;
l=
V0cosα/k-
gcosα/k2sinα;
h= V0sinα (1- g/k V0sinα) /k + g ln(g/k V0sinα)/k2
44.В
гамильтоновой механике каноническое
преобразование — это любое преобразование
фазового пространства системы,
сохраняющее его симплектическую
структуру.Канонические преобразования
обычно задаются производящей функцией.
Пусть F(q,Q,t) — произвольная невырожденная
функция старых координат, новых координат
и времени:
![]() Тогда
она задаёт каноническое преобразование
по правилу
Тогда
она задаёт каноническое преобразование
по правилу![]()
![]()
![]() где
(q,p) — старые координаты и импульсы
системы, а (Q,P) — новые координаты и
импульсы.Действие, выраженное как
функция координат и импульсов конечной
точки
где
(q,p) — старые координаты и импульсы
системы, а (Q,P) — новые координаты и
импульсы.Действие, выраженное как
функция координат и импульсов конечной
точки![]() задаёт
каноническое преобразование гамильтоновой
системы.
задаёт
каноническое преобразование гамильтоновой
системы.
