21 Модель Максвела

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет имени Ф.Скорины»

Физический факультет

Отчет по лабораторной работе

№ 21

ИЗУЧЕНИЕ НА МЕХАНИЧЕСКОЙ МОДЕЛИ

РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА ПО СКОРОСТЯМ

Выполнили:

Студенты группы Ф-14

Завольский Егор и

Холодилина Татьяна

Лабораторная работа № 21

ИЗУЧЕНИЕ НА МЕХАНИЧЕСКОЙ МОДЕЛИ

РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА ПО СКОРОСТЯМ

Цель работы: получить и изучить на механической модели распределение

частиц, аналогичное распределению Максвелла молекул газа по скоростям, определить вероятную скорость частиц.

Приборы и принадлежности: установка для изучения закона

распределения Максвелла, пшено, линейка.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Молекулы в газе движутся хаотично, поэтому абсолютные значения их скоростей не совпадают друг с другом. Чтобы описать распределение молекул газа по скоростям, будем рассматривать вероятность того, что молекула имеет скорость, абсолютная величина которой лежит в интервале от 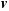до 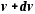. Каждая из трех составляющих вектора скорости по осям координат является случайной величиной, распределенной по нормальному закону Гаусса:

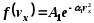
где 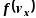-- плотность вероятности, А₁ и _некоторые константы, которые легко определить из условия:

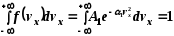
Вероятность того, что составляющие скорости молекулы находятся одновременно в интервалах

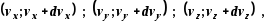
зависит только от модуля 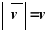, или что то же самое, от квадрата скорости. Вместо квадрата составляющих скорости в качестве аргумента берут соответствующие им значения кинетических энергий

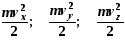и полную кинетическую энергию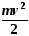

тогда уравнение (1) может быть переписано в виде

(1)

где A₂ и _ - новые постоянные;

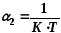
где К – постоянная Больцмана, Т – температура по шкале Кельвина. Таким образом формула (1) примет вид

Чтобы получить закон распределения Максвелла по скоростям, необходимо проинтегрировать (3) по всем значениям скоростей, лежащим внутри тонкого шарового слоя радиусом v и толщиной dv. Объем этого слоя равен 4v²dv.

Следовательно , функцию распределения по абсолютным значениям скоростей можно получить из функции (3), умножив ее на 4v². Тогда

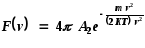
Внесем 4в значение постоянной А₂ и введем А = 4А₂. Тогда

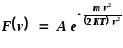
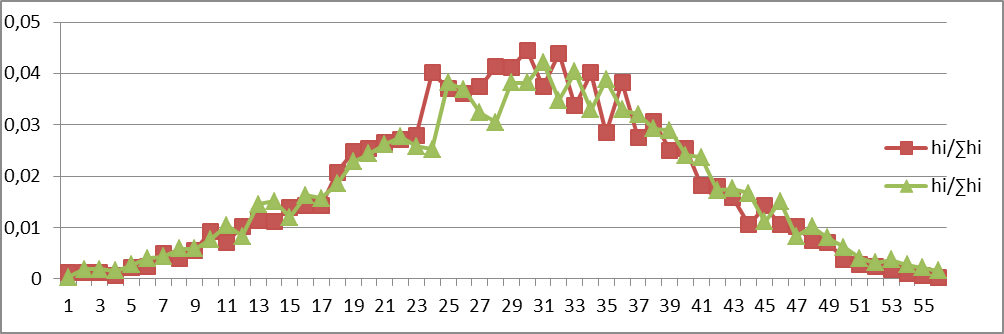
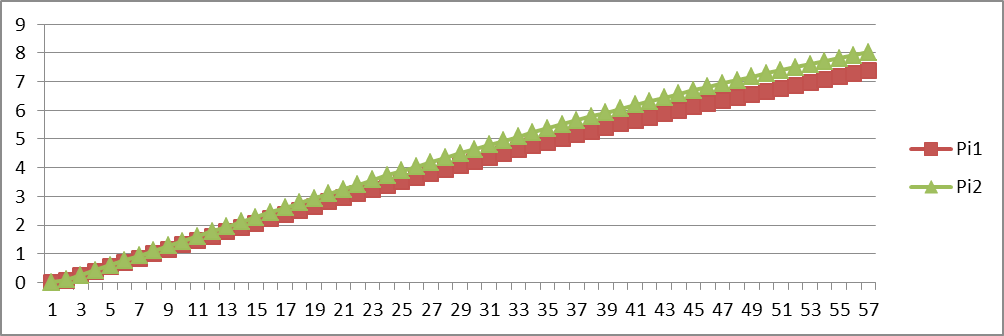
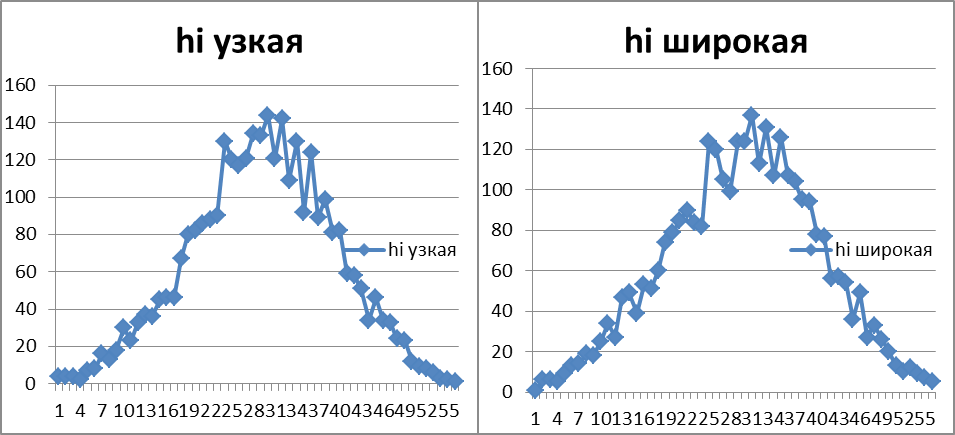
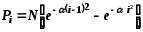, N=∑i

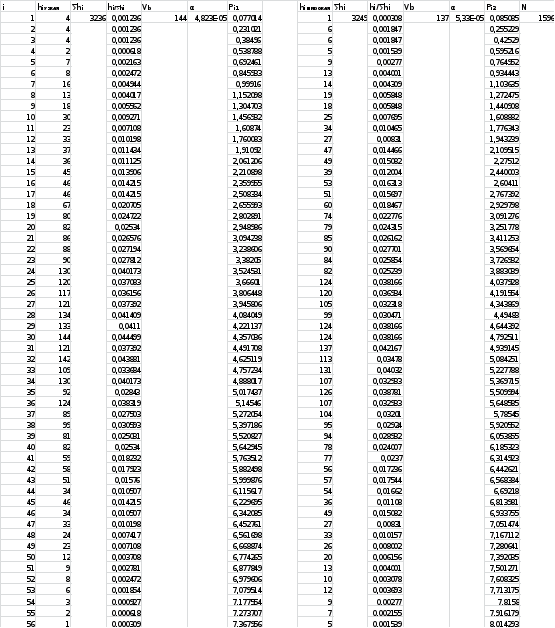
Вывод: получили и изучили на механической модели распределение частиц аналогичное распределению Максвелла молекул газа по скоростям, определили вероятную скорость частиц, построили графики распределения, источниками погрешностей служат случайный характер движения частиц и различные внешние факторы, сравнили полученные результаты с распределением Максвелла, общая картина представляется довольно схожей.