
Краткий конспект лекций
ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Краткий конспект лекций по аналитической геометрии предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.
ОГЛАВЛЕНИЕ
|
Введение |
4 |
|
Лекция 1. Метод координат |
5 |
|
Лекция 2. Прямые на плоскости |
8 |
|
Лекция 3. Прямые в пространстве |
12 |
|
Лекция 4. Плоскости в пространстве |
14 |
|
Лекция 5. Кривые второго порядка |
18 |
|
Контрольные вопросы |
23 |
ВВЕДЕНИЕ
Краткий конспект лекций по аналитической геометрии предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.
Лекция 1
Метод координат
Контрольные вопросы:
1. Расстояние между
двумя точками
![]() и
и![]() на плоскости.
на плоскости.
2. Нахождение
координат
![]() точки М, делящей в отношении λ заданный
отрезок.
точки М, делящей в отношении λ заданный
отрезок.
3. Нахождение площади треугольника по координатам его вершин.
Метод координат заключается в установлении соответствия между точками прямой (плоскости, пространства) и их координатами – действительными числами при помощи системы координат.
Прямоугольная система координат Оху на плоскости задается двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок.
Координатами точки
М в системе координат Оху
называются координаты радиус-вектора
![]() .
.
Расстояние между
двумя точками
![]() и
и![]() на плоскости вычисляется по формуле
на плоскости вычисляется по формуле
![]() . (1)
. (1)
Координаты
![]() точки М, делящей в заданном отношении
λ отрезок
АВ,
где
точки М, делящей в заданном отношении
λ отрезок
АВ,
где
![]() ,
,![]() ,
,![]() ,
находятся по формулам
,
находятся по формулам
![]() ,
,
![]() . (2)
. (2)
Если λ = 1, т.е. точка М делит отрезок АВ пополам, получаются формулы координат середины отрезка
![]() ,
,
![]() . (3)
. (3)
Площадь треугольника
с вершинами
![]() ,
,![]() ,
,![]() вычисляется по формуле
вычисляется по формуле
![]() ,
где
,
где
![]() . (4)
. (4)
Пример 1. Отрезок AB четырьмя точками разделён на пять равных частей. Определить координату ближайшей к A точки деления, если A(-3), B(7).
Решение.
Пусть
![]() - искомая точка; тогда
- искомая точка; тогда![]() .
.
Следовательно, по
формуле
![]() находим
находим![]() ,
т.е.С(-1).
,
т.е.С(-1).
Пример 2. Известны точки А(1), В(5) – концы отрезка АВ; вне этого отрезка расположена точка С, причем ее расстояние от точки А в три раза больше расстояния от точки В. Определить координату точки С.
Решение.
Отметим, что
![]() .
Таким образом,
.
Таким образом,
![]() ,
т.е. C(7).
,
т.е. C(7).
Пример 3.
Определить
расстояние между точками
![]() и
и![]() .
.
Решение.
По формуле (1) получим
![]()
Пример 4. Даны
вершины треугольника АВС:
![]() ,
,![]() ,
,![]() .
Определить координаты точки пересечения
медиан треугольника.
.
Определить координаты точки пересечения
медиан треугольника.
Решение.
Найдем координаты
точки D
– середины отрезка АВ;
имеем
![]() ,
,![]() .
ТочкаМ,
в которой пересекаются медианы, делит
отрезок СD в
отношении 2:1,
считая от вершины С.
Следовательно, координаты точки М
можно определить по формулам
.
ТочкаМ,
в которой пересекаются медианы, делит
отрезок СD в
отношении 2:1,
считая от вершины С.
Следовательно, координаты точки М
можно определить по формулам
![]() ,
,
![]() ,
,
т.е.
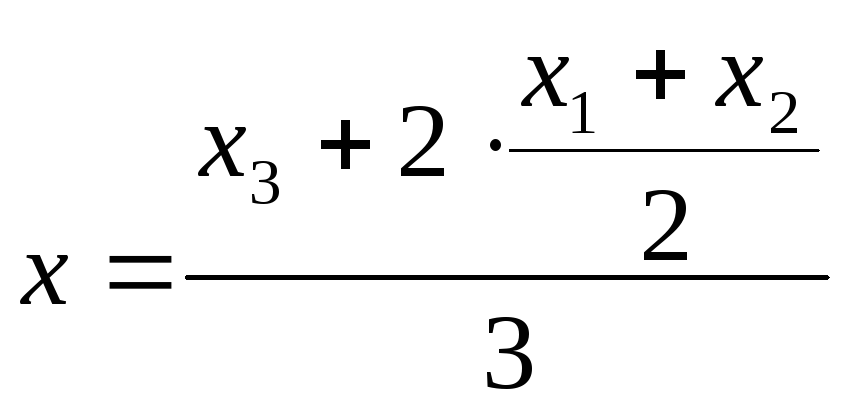 ,
,
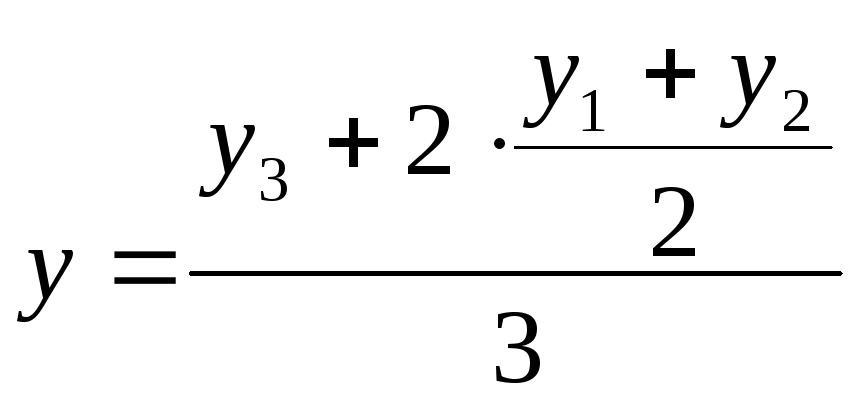 .
.
В результате получаем
![]() ,
,
![]() .
.
Пример 5.
Определить
площадь треугольника с вершинами:
![]() ,
,![]() ,
,![]() .
.
Решение.
Используя формулу (4), получим
![]() (кв.ед.).
(кв.ед.).
Пример 6.
Составить уравнение прямой, проходящей
через точку M(-2;-5)
параллельно прямой
![]() .
.
Решение.
Разрешив последнее
уравнение относительно y,
получим
![]() .
Следовательно, в силу условия параллельности
угловой коэффициент искомой прямой
равен -3/4. Воспользовавшись уравнением
.
Следовательно, в силу условия параллельности
угловой коэффициент искомой прямой
равен -3/4. Воспользовавшись уравнением![]() ,
получаем
,
получаем![]() ,
т.е.
,
т.е.![]() .
.
Пример 7. Даны вершины треугольника: А(2; 2), В(-2; -8) и С (-6;-2). Составить уравнение медиан треугольника.
Решение.
Находим координаты середин сторон ВС, АС и АВ:
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,![]()
Уравнения медиан находим с помощью уравнения прямой, проходящей через две данные точки. Уравнение медианы АА1:
![]() ,
или
,
или
![]() ,
т.е.
,
т.е.![]() .
.
Находим уравнение
медианы ВВ1:
поскольку точки В(-2;
-8) и В1(-2;0)
имеют одинаковые абсциссы, медиана ВВ1
параллельна оси ординат. Ее уравнение
![]() .
.
Уравнение медианы
СС1:
![]() ,
или
,
или![]() .
.
Пример 8. Даны вершины треугольника: А(0; 1), В(6; 5) и С(12; -1). Составить уравнение высоты треугольника, проведенной из вершины С.
Решение.
По формуле
![]() найдем угловой коэффициент стороныАВ;
имеем
найдем угловой коэффициент стороныАВ;
имеем
![]() .
В силу условия перпендикулярности
угловой коэффициент высоты, проведенной
их вершиныС,
равен -3/2. уравнение этой высоты имеет
вид
.
В силу условия перпендикулярности
угловой коэффициент высоты, проведенной
их вершиныС,
равен -3/2. уравнение этой высоты имеет
вид
![]() ,
или
,
или![]() .
.
Лекция 2
