
ИДЗ_РЯДЫ_АЛЬБ
.docИндивидуальные домашние задания
ИДЗ – 1 Числовые и функциональные ряды
1 Найти суммы рядов:
1.1
![]() . 1.2
. 1.2
![]() .
.
1.3
![]() . 1.4
. 1.4
![]() .
.
1.5
![]() . 1.6
. 1.6
![]() .
.
1.7
![]() . 1.8
. 1.8
![]() .
.
1.9
![]() . 1.10
. 1.10
![]() .
.
1.11
![]() . 1.12
. 1.12
![]() .
.
1.13
![]() . 1.14
. 1.14
![]() .
.
1.15
![]() . 1.16
. 1.16
![]() .
.
1.17
![]() . 1.18
. 1.18
![]() .
.
1.19
![]() . 1.20
. 1.20
![]() .
.
1.21
![]() . 1.22
. 1.22
![]() .
.
1.23
![]() . 1.24
. 1.24
![]() .
.
1.25
![]() . 1.26
. 1.26
![]() .
.
1.27
![]() . 1.28
. 1.28
![]() .
.
1.29
![]() . 1.30
. 1.30
![]() .
.
2 Исследовать сходимость рядов с неотрицательными членами:
2.1
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.2
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.3
а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.4
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.5
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.6
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.7
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.8
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.9
а) , б)
, б)
![]() ,
в)
,
в)![]() .
.
2.10
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.11
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.12
а)
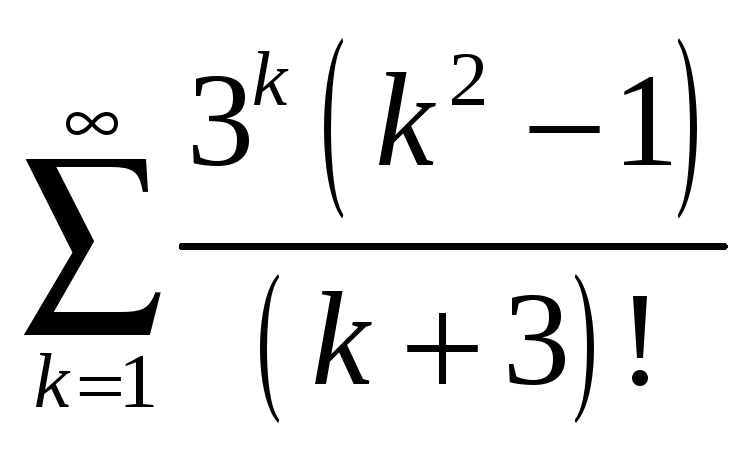 ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.13
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.14
а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.15
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.16
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.17
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.18
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.19
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.20
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.21
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.22
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.23
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.24
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.25
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.26
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.27
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.28
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.29
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
2.30
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
3 Исследовать
сходимость рядов. В случае сходимости
ряда, вычислить его сумму с точностью
![]() .
.
3.1
![]() ,
,
![]() . 3.2
. 3.2
![]() ,
,
![]() .
.
3.3
![]() ,
,
![]() . 3.4
. 3.4
![]() ,
,
![]() .
.
3.5
![]() ,
,
![]() . 3.6
. 3.6
![]() ,
,
![]() .
.
3.7
![]() ,
,
![]() . 3.8
. 3.8
![]() ,
,
![]() .
.
3.9
![]() ,
,
![]() . 3.10
. 3.10
![]() ,
,
![]() .
.
3.11
![]() ,
,
![]() . 3.12
. 3.12
![]() ,
,
![]() .
.
3.13
![]() ,
,
![]() . 3.14
. 3.14
![]() ,
,
![]() .
.
3.15
![]() ,
,
![]() . 3.16
. 3.16
![]() ,
,
![]() .
.
3.17
![]() ,
,
![]() . 3.18
. 3.18
![]() ,
,
![]() .
.
3.19
![]() ,
,
![]() . 3.20
. 3.20
![]() ,
,
![]() .
.
3.21
![]() ,
,
![]() . 3.22
. 3.22
![]() ,
,
![]() .
.
3.23
![]() ,
,
![]() . 3.24
. 3.24
![]() ,
,
![]() .
.
3.25
![]() ,
,
![]() . 3.26
. 3.26
![]() ,
,
![]() .
.
3.27
![]() ,
,
![]() . 3.28
. 3.28
![]() ,
,
![]() .
.
3.29
![]() ,
,
![]() . 3.30.
. 3.30.
![]() ,
,
![]() .
.
4 Найти область сходимости функциональных рядов:
4.1
![]() . 4.2
. 4.2
![]() .
.
4.3
![]() . 4.4
. 4.4
![]() .
.
4.5
![]() . 4.6
. 4.6
![]() .
.
4.7
![]() . 4.8
. 4.8
![]() .
.
4.9
![]() . 4.10
. 4.10
![]() .
.
4.11
![]() . 4.12
. 4.12
![]() .
.
4.13
![]() . 4.14
. 4.14
![]() .
.
4.15
![]() . 4.16
. 4.16
![]() .
.
4.17
![]() . 4.18.
. 4.18.
![]() .
.
4.19
![]() . 4.20
. 4.20
![]() .
.
4.21
![]() . 4.22
. 4.22
![]() .
.
4.23
![]() . 4.24
. 4.24
![]() .
.
4.25
![]() . 4.26
. 4.26
![]() .
.
4.27
![]() . 4.28
. 4.28
![]() .
.
4.29
![]() . 4.30
. 4.30
![]() .
.
5 Найти область сходимости и область равномерной сходимости функциональных рядов:
5.1
![]() . 5.2
. 5.2
![]() .
.
5.3
![]() . 5.4
. 5.4
![]() .
.
5.5
![]() . 5.6
. 5.6
![]() .
.
5.7
![]() . 5.8
. 5.8
![]() .
.
5.9
 . 5.10
. 5.10
![]() .
.
5.11
 . 5.12
. 5.12
![]() .
.
5.13
![]() . 5.14
. 5.14
![]() .
.
5.15
![]() . 5.16
. 5.16
![]() .
.
5.17
![]() . 5.18
. 5.18
![]() .
.
5.19
![]() . 5.20
. 5.20
![]() .
.
5.21
![]() . 5.22
. 5.22
 .
.
5.23
![]() . 5.24
. 5.24
![]() .
.
5.25
![]() . 5.26
. 5.26
![]() .
.
5.27
![]() . 5.28
. 5.28
![]() .
.
5.29
![]() . 5.30
. 5.30
![]() .
.
ИДЗ - 2 Ряды Фурье
1
На промежутке
![]() разложить в ряд Фурье а) по косинусам,
б) по синусам функции (нарисовать в
обоих случаях графики суммы рядов для
разложить в ряд Фурье а) по косинусам,
б) по синусам функции (нарисовать в
обоих случаях графики суммы рядов для
![]() 1,
2, 3):
1,
2, 3):
1.1
![]() =
4 x
+ 6. 1.2
=
4 x
+ 6. 1.2
![]() = 6 x
– 3.
= 6 x
– 3.
1.3
![]() =
2 x
+ 8. 1.4
=
2 x
+ 8. 1.4
![]() = – x
+ 2.
= – x
+ 2.
1.5
![]() = 3 x
+ 5. 1.6
= 3 x
+ 5. 1.6
![]() = – x
+ 1.
= – x
+ 1.
1.7
![]() = 4 x
+ 3. 1.8
= 4 x
+ 3. 1.8
![]() = 9 x
+ 4.
= 9 x
+ 4.
1.9
![]() = 5 x
+ 5. 1.10
= 5 x
+ 5. 1.10
![]() = 2 x
+ 7.
= 2 x
+ 7.
1.11
![]() = 3 x
+
6. 1.12
= 3 x
+
6. 1.12
![]() = 7x
– 6.
= 7x
– 6.
1.13
![]() = 3 x
– 6. 1.14
= 3 x
– 6. 1.14
![]() = 2x
+ 6.
= 2x
+ 6.
1.15
![]() = 3 x
+ 6. 1.16
= 3 x
+ 6. 1.16
![]() =
4 x
– 6.
=
4 x
– 6.
1.17
![]() = 2 x
– 6. 1.18
= 2 x
– 6. 1.18
![]() =
x
+ 6.
=
x
+ 6.
1.19
![]() =
–9
x
+ 1. 1.20
=
–9
x
+ 1. 1.20
![]() = 9 x
– 6.
= 9 x
– 6.
1.21
![]() = 2 x
– 9. 1.22
= 2 x
– 9. 1.22
![]() =
3 x
– 9.
=
3 x
– 9.
1.23
![]() = x
+ 5. 1.24
= x
+ 5. 1.24
![]() = –8 x
– 1.
= –8 x
– 1.
1.25
![]() = 3 x
+ 1. 1.26
= 3 x
+ 1. 1.26
![]() = 8 x
+ 3.
= 8 x
+ 3.
1.27
![]() = 5
x
–
7. 1.28
= 5
x
–
7. 1.28
![]() =
4 x
+
6.
=
4 x
+
6.
1.29
![]() =
–
x
+
6. 1.30
=
–
x
+
6. 1.30
![]() = 5x
+ 6.
= 5x
+ 6.
2
На отрезке
![]() разложить в ряд Фурье функции:
разложить в ряд Фурье функции:
2.1
![]() = 2│x│–
3. 2.2
= 2│x│–
3. 2.2
![]() = 2│x│+
1.
= 2│x│+
1.
2.3
![]() = │x│–
5. 2.4
= │x│–
5. 2.4
![]() = –3│x│+
2.
= –3│x│+
2.
2.5
![]() = 4│x│+
8. 2.6
= 4│x│+
8. 2.6
![]() = –│x│–
6.
= –│x│–
6.
2.7
![]() = –5│x│+
1. 2.8
= –5│x│+
1. 2.8
![]() = –2│x│–
4.
= –2│x│–
4.
2.9
![]() = 3│x│+
7. 2.10
= 3│x│+
7. 2.10
![]() = –2│x│+
5.
= –2│x│+
5.
2.11
![]() = 7│x│–
1. 2.12
= 7│x│–
1. 2.12
![]() = │x│+
9.
= │x│+
9.
2.13
![]() = │x│+
1. 2.14
= │x│+
1. 2.14
![]() = 5│x│.
= 5│x│.
2.15
![]() = –6│x│+2. 2.16
= –6│x│+2. 2.16
![]() = –3│x│+
1.
= –3│x│+
1.
2.17
![]() = 5│x│+
2. 2.18
= 5│x│+
2. 2.18
![]() = –│x│–
6.
= –│x│–
6.
2.19
![]() = │x│–
8. 2.20
= │x│–
8. 2.20
![]() = –4│x│+
1.
= –4│x│+
1.
2.21
![]() = –5│x│+
7. 2.22
= –5│x│+
7. 2.22
![]() = 2│x│–
8.
= 2│x│–
8.
2.23
![]() = 7│x│+
2. 2.24
= 7│x│+
2. 2.24
![]() = │x│+
8.
= │x│+
8.
2.25
![]() = –3│x│+
7. 2.26
= –3│x│+
7. 2.26
![]() = –│x│+
1.
= –│x│+
1.
2.27
![]() = 5│x│+
2. 2.28
= 5│x│+
2. 2.28
![]() = │x│–
6.
= │x│–
6.
2.29
![]() = │x│–
8. 2.30
= │x│–
8. 2.30
![]() = 4│x│+
1.
= 4│x│+
1.
3
Разложить в ряд Фурье на отрезке
![]() функции (нарисовать
графики суммы рядов для
функции (нарисовать
графики суммы рядов для
![]() 1,
2, 3):
1,
2, 3):
3.1 3.2
![]()

![]()

3.3 3.4
![]()

![]()

3.5 3.6
![]()

![]()

3.7 3.8
![]()

![]()

