Вязкость растворов полимеров

Вязкость жидкостей можно для простоты определить как сопротивление жидкости передвижению одного её слоя относителоьно другого при сдвиге, растяжении и других видах деформации.

Вязкость характеризуют интенсивностью работы, затрачиваемой на осуществление течения газа или жидкости с определённой скоростью. При ламинарном сдвиговом течении жидкости между двумя плоскопараллельными пластинками, верхняя из которых движется с постоянной скоростью v под действием силы F , а нижняя неподвижна, слои жидкости перемещаются с разными скоростями: от максимальной у верхней пластинки до нуля у нижней. При этом касательное напряжение τ = , а скорость деформации γ = , где S – площадь пластинок, Н – расстояние между пластинками. Если между τ и γ имеется линейная зависимость, жидкость называется ньютоновской, а отношение τ : γ называется динамической вязкостью (или просто вязкостью) η. Жидкости для которых эта зависимость является нелинейной называются неньютоновскими.

Истинные растворы НМС являются ньютоновскими жидкостями, для них вязкость описывается уравнением Ньютона:

F = η∙s∙

где F – сила, необходимая для возникновения перемещения двух соседних слоёв раствора; du / dx –градиент скорости; η – коэффициент вязкости. Вязкость, вычисленная по уравнению Ньютона, не зависит от напряжения сдвига, определяемой действующей силой, типом вискозиметра и т.д. Величина вязкости при данной температуре для НМС является инвариантной (неменяющейся) характеристикой.

Вязкость золей (η) описывается уравнением Эйнштейна:

η = η₀(1 + 2,5φ)

где η₀ – вязкость дисперсионной среды; φ – объёмная концентрация дисперсной фазы.

[Эйнштейн Альберт (1879-1955), физик-теоретик, один из основателей современной физики, иностранный ч.-к. Российской АН. Эйнштейн создал теорию относительности, является автором основополагающих трудов по квантовой теории света: ввёл понятие фотона (1905), установил законы фотоэффекта и многое другое. Развил статистическую теорию броуновского движения, создал квантовую статистику и т.д. С 1933 г работал над проблемами космологии и единой теории поля. Нобелевская премия (1921)].

Уравнение Эйнштейна пригодно только при условии, что взвешанные в жидкости частицы являются твёрдыми шарообразными телами, концентрация дисперсной фазы сравнительно невелика и между частицами отсутствуют взаимодействия.

Вязкость растворов, содержащих макромолекулы, обычно выше вязкости растворов низкомолекулярных веществ и вязкости коллоидных систем при одной и той же концентрации. Например, вязкость 1%-ного раствора каучука в бензине в 18 раз выше вязкости чистого бензина.

Вязкость растворов ВМС не является постоянной величиной; она зависит от условий измерения, в первую очередь от скорости движения раствора в вискозиметре. Вычисленная по уравнению Ньютона вязкость в этом случае является чисто условной величиной и называется эффективной вязкостью. Растворы ВМС являются неньютоновскими жидкостями, так как они не обладают постоянной вязкостью. У растворов ВМС наблюдается аномалия вязкости.

В растворах полимеров происходит образование пространственных структур, образуемых сцеплением макромолекул, что и вызывает резкое повышение вязкости. При течении растворов полимеров работа затрачивается не только на преодоление истинной (ньютоновской) вязкости, но и на разрушение структуры раствора.

Вязкость растворов ВМС зависит от условий определения, в частности от напряжения сдвига. Это связано с тем, что одни и те же макромолекулы могут находиться в различных конформационных состояниях; от линейных до глобул.

{Напомним, что: а) различные геометрические формы молекул, переходящие друг в друга путём вращения вокруг σ-связей, называются конформациями; б) глобулы – это коллоидные частицы сферической формы или макромолекулы, свёрнутые в клубок). }.

По этой причине вязкость концентрированных растворов ВМС может быть неодинаковой (анизотропной) в различных направлениях. Вязкость макромолекул с выпрямленными и ориетированными хаотично по отношению к направлению движения звеньями выше, чем вязкость макромолекул, которые имеют форму клубка или глобул.

Если вязкий раствор ВМС продавливать под давлением через капилляр, то макромолекулы будут ориентироваться и вытягиваться в капилляре, а поэтому наблюдаемая вязкость раствора снижается.

Вязкость растворов ВМС в значительной степени зависит от температуры и свойств растворителя. Растворители способны влиять на конформационную форму макромолекул и за счёт этого изменять вязкость одного и того полимера в разных растворителях. Таким образом, вязкость растворов ВМС определяется природой полимера и природой растворителя.

Точное измерение абсолютной вязкости растворов полимеров затруднительно. Поэтому для растворов ВМС различают относительную, удельную, приведённую и характеристическую вязкость.

Относительная вязкость – это отношение вязкости раствора полимера η_р к вязкости растворителя η₀

η_отн =

Относительную вязкость можно определить по времени истечения раствора ВМС t_p и растворителя t₀ через калиброванное отверстие вискозиметра:

η_отн =

Относительная вязкость является мерой изменения вязкости раствора по сравнению с вязкостью чистого растворителя. Для растворов макромолекул относительная вязкость η_отн обычно больше единицы.

Удельная вязкость – отражает возрастание относительной вязкости по сравнению с единицей:

η_уд = η_отн – 1.

Чтобы учесть влияние концентрации раствора, т.е. оценить, насколько велика удельная вязкость, отнесённая к единице концентрации растворённого вещества, η_уд делят на с. Полученная величина называется приведённой вязкостью. Её величина выражается следующей формулой

η_привед =

Так как η_уд сама зависит от концентрации, приходится вводить ещё одну величину [η] (собственную вязкость), которую получают путем экстраполяции зависимости η_уд / с от концентрации раствора с.

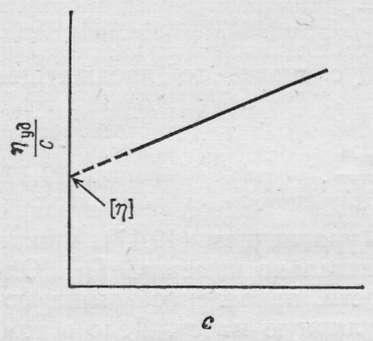
Величину [η] называют характеристической вязкостью или предельным числом вязкости.

[η] = lim η_уд / с

C → 0

Характеристическую вязкость определяют на основании вискозиметрических измерений, используя значения относительной, удельной и приведённой вязкости в качестве вспомогательных величин.

Характеристическая вязкость для данной пары веществ (растворитель – полимер) является условной, но постоянной величиной, которая не зависит от концентрации растворителя и конформационных состояний макромолекул.

В 1930 г Штаудингером было предложено полезное соотношение между молекулярной массой и характеристической вязкостью.

[η] = KM

Это соотношение имело ряд недостатков. Поэтому позже оно было модифицировано. В настоящее время оно известно, как уравнение Марка-Куна-Хаувинка и имеет следующий вид:

[η] = KM ^α,

где К – постоянная величина, экспериментально определяемая для данных макромолекул и растворителя. Показатель степени α зависит от формы макромолекул. Для белков компактной структуры – глобулярных белков – он составляет около 0,5. Для молекул, находящихся в конформации беспорядочного клубка, показатель степени возрастает до 2. Молекулярная масса, определяемая по уравнению Марка-Куна-Хаувинка, называется средневязкостной молекулярной массой М_η.

Величина характеристической вязкости позволяет определить как относительную молекулярную массу полимера, так и размеры и форму его макромолекул. Например, если растворы белков характеризуются величинами [η, лежащими между 3,0 и 4,0 см³/г, то столь малое значение данных величин указывает на глобулярную, весьма компактную структуру этих белков, форма которых незначительно отличается от сферы. Большие значения [η указывают либо на высокую степень асимметричности белков, либо на большой объём, занимаемый данными белками в растворе.