37. Распределение скоростей по сечению трубы при ламинарном режиме.

При ламинарном режиме движение частиц жидкости происходит параллельно стенкам трубы без поперечных перемещений, т.е. параллельно слоям. При этом слой жидкости, непосредственно соприкасающаяся со стенкой, неподвижен, вследствие прилипания к ней, т.е. скорость движения частиц на стенке равна 0.

Используем гипотезу Ньютона для выражения сил трения.

где - коэффициент вязкости,- градиент скорости.

Приравнивая между собою иполучаем:

Интегрируя это уравнение, получим:

Постоянная интегрирования определяется из условия, что скорость у стенки = 0, получаем:и поэтомуМаксимальной является скорость приr = 0 , т.е. на оси трубы и обозначаем через и равна:

Следовательно, выражение для скорости в любой точке потока можно представить через осевую в виде:

Графически это можно изобразить как показано на рисунке. Рисунок отражает параболический закон распределения скоростей в круглой трубе при ламинарном движении жидкости называемый законом Стокса.

38. Потери энергии при ламинарном движении жидкости.

При ламинарном режиме движение частиц жидкости происходит параллельно стенкам трубы без поперечных перемещений , т.е. параллельными слоями. Можно представить что поток жидкости состоит из концентрических цилиндров , движущихся один относительно другого с разными скоростями. При этом слой жидкости , соприкасающийся со стенками трубы остается неподвижным (гипотеза “прилипания”).

Из уравнения нахождения максимальной скорости см. 17 билет. Следует, что величина равна:

Зная величину , найдем из формулы (1) (см. приложение) выражение для потерь напора на трение:

формула (1)

Теперь найдем чему равен :

Мы знаем, что средняя скорость потока при ламинарном режиме равна половине осевой:

Подставим в ранее выведенную формулу для:

или, введя вместо радиуса диаметр трубы и выражая абсолютную вязкость через кинематическую:, получим:

Из этой формулы видно, что потери напора при ламинарном движении пропорциональны первой степени средней скорости или расхода жидкости.

Эту формулу можно представить в другом виде, если учесть, что

Подставим:

или, введя обозначение окончательно получим:

где называетсякоэффициентом гидравлического сопротивления. Все выражение наз. формулой Дарси-Вейсбаха.

39. Механизм и структура турбулентного потока.

Измерения скорости движения частиц жидкости в фиксирован­ных точках турбулентного потока показали, что в каждый момент времени изменяется как ее величина, так и направление. Беспоря­дочный характер движения частиц жидкости — основная особен­ность турбулентности. Но при этом скорость, давление, температура по-прежнему являются непрерывными функциями пространства и времени. Несмотря на беспорядочность в изменениях скорости, всегда имеется основное на­правление движения, ка­ким является течение вдоль оси трубы.

Скорость, измеренную в данный момент времени, называют мгновенной. Мгновенную скорость можно разложить на три составляющие: осевую и поперечные- в плоскости живого сечения потока.

На рисунке показаны типичные графики изменения мгновенных скоростей во времени по каждому из направлений. Как видно из графиков, несмотря на кажущуюся беспорядочность изменений скорости, осредненное ее значение за достаточно большой промежуток времени остается все же постоянным. Поэтому при изучении турбулентных потоков вводятся в рассмотрение осредненные значения – притом не только скоростей, но также давления, плотности, температуры и т.д.

Отклонение мгновенной скорости от осредненной называют пульсацией скорости, которая определяется как разность

Среднее значение скорости:

Поперечные осредненные скорости равны 0

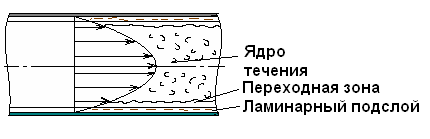
По этой схеме: у стенок образуется весьма тонкий слой жидкости, называемый ламинарным подслоем, в котором движение жидкости происходит по законам ламинарного режима; основная центральная часть потока (ядро), отделенная от этого подслоя переходной зоной, движется турбулентно с почти одинаковой для всех частиц жидкости осредненной скоростью.

Характеристики турбулентного движения могут меняться в зависимости не только от расхода жидкости, диаметра труб и вязкости жидкости, но также в зависимости от состояния внутренней поверхности трубы.