Шпоры по гидре / мои билеты / 25-36

25. Геометрический и энергетический смысл ур-я Бернулли для струйки идеальной жидкости.

z₁ + P₁/γ + ν₁² / 2g = z₂ + P₂/γ + ν₂² / 2g (γ = ρg – объемный вес )

Геометрич.смысл:

z – геометрич. высота (или

геометрич. напор), (высота

положения) центров тяжести

живых сечений элементарной

струйки над плоскостью

сравнения.

P/γ – пьезометрич. высота (или

пьезометрич. напор), (высота давл-я) – соответствует высота

такого столба жид-сти с объемн. весом γ , кот. у своего

основания создает давл-е Р.

z + P/γ – гидростатич. напор (высота).

ν² / 2g – скоростная высота (скор-ной напор)

z + P/γ + ν² / 2g = H = const (вдоль струйки)–

гидродинамический (полный) напор (высота).

Геометрич. смысл: для идеальн. движ-ся жид-сти сумма трех

напоров(высот) – геометрич., пьезометрич. и скоростного есть

величина постоянная вдоль струйки. Т.о. напорная пл-сть в

идеал. жид-сти есть пл-сть горизонтальная.

Энергетич. смысл

z – удельная (отнесенная к единице массы) потенц. энергия

положения частицы в сечениях.

P/γ – удельная потенц. энергия давл-я.

z + P/γ – удельная потенц. энергия (условно).

ν² / 2g - удельная кинетич. энергия

26. Геометрический и энергетический смысл ур-я Бернулли для струйки реальной (вязкой) жидкости.

z₁ + P₁/γ + ν₁² / 2g =z₂ + P₂/γ + ν₂² / 2g + h_п (γ = ρg–объемный вес)

Геометрич.смысл:

z – геометрич. высота (или

геометрич. напор), (высота

положения) центров тяж-ти

живых сечений элементар.

струйки над плоскостью

сравнения.

P/γ – пьезометрич. высота

(или пьезометрич. напор),

(высота давл-я) – соответствует высота такого столба жид-сти с

объемн. весом γ , кот. у своего основания создает давл-е Р.

z + P/γ – гидростатич. напор (высота).

ν² / 2g – скоростная высота (скор-ной напор)

z + P/γ + ν² / 2g = H ≠ const – гидродинамический (полный)

напор (высота) уменьшается по длине струйки, т.о. геометрич.

смысл закл. в том, что в струйке реальной(вязкой) жид-сти

напорная линия явл-ся наклонной, нисходящей.

h_п = h_дл + h_мест = H₁ – H₂ – потеря напора м/у рассматриваемыми

сечениями струйки.

h_дл – потери напора на трение по длине;

h_мест – местные потери напора.

Энергетич. смысл

z – удельная (отнесенная к единице массы) потенц. энергия

положения частицы в сечениях.

P/γ – удельная потенц. энергия давл-я.

z + P/γ – удельная потенц. энергия (условно).

ν² / 2g - удельная кинетич. энергия

27. Ур-ние Бернулли для струйки реальной (вязкой) жид-сти.

На практике приходиться

обращаться с жид-стью

вязкой, обладающей рядом

св-в, кот. не учитываются

при исполь-нии понятия об

идеал. жид-сти.

Вязкость реальной жид-сти –

обуславливает возник-ние

сопрот-я движ-ю и, как следствие,

вызывает потерю части энергии, содержащейся в движущейся

струйке.

В вязкой жид-сти энергия по длине струйки уменьшается,

переходя в рез-те трения в тепловую.

Соотношение значений полной энергии в сечениях:

z₁ + P₁/γ + ν₁² / 2g > z₂ + P₂/γ + ν₂² / 2g

Тогда пусть разность полных удел. энергий в сечениях:

h_п = (z₁ + P₁/γ + ν₁² / 2g ) – ( z₂ + P₂/γ + ν₂² / 2g)

Откуда:

z₁ + P₁/γ + ν₁² / 2g = z₂ + P₂/γ + ν₂² / 2g + h_п (γ = ρg –объемный

вес)

z + P/γ + ν² / 2g = H ≠ const – гидродинамический (полный)

напор (высота) уменьшается по длине струйки, т.о. в струйке

реальной(вязкой) жид-сти напорная линия явл-ся наклонной,

нисходящей.

h_п = h_дл + h_мест = H₁ – H₂ – потеря напора м/у рассматриваемыми

сечениями струйки.

h_дл – потери напора на трение по длине;

h_мест – местные потери напора.

29. Геометрический и энергетический смысл ур-я Бернулли для потока реальной (вязкой) жидкости.

z₁ + P₁/γ + α₁ν_ср1² / 2g = z₂ + P₂/γ + α₂ν_ср2² / 2g + h_п (γ = ρg –

объемный вес)

Геометрич.смысл:

z – геометрич. высота (или

геометрич. напор), (высота

положения) центров тяж-ти

живых сечений потока над

плоскостью сравнения.

P/γ – пьезометрич. высота

(или пьезометрич. напор),

(высота давл-я) – соответствует высота такого столба жид-сти с

объемн. весом γ , кот. у своего основания создает давл-е Р.

z + P/γ – гидростатич. напор (высота).

αν_ср² / 2g – скоростная высота (скор-ной напор), где α – коэф-т

Кориолиса, кот. харак-ет неравномерность распред-я местных

скоростей по живому сечению. В связи с этим вводится понятие

средн. ск-сти потока – это ск-сть, с которой должны были бы

двигаться все частицы(или струйки) жид-сти через данное

живое сечение, чтобы раход всего потока был бы равен

расходу, соответствующему действительным ск-стям этих

частиц (или струек). Значение α зависит от вязкости, ск-сти

движ-я жид-сти, шерох-сти стенок трубо-да, режимов движ-я

жид-сти (α=1 – для движ-я идеал. жид-сти, 1<α<2 – для турбул.

режима, α=2 – для ламинар.)

z + P/γ + αν_ср² / 2g = Н – гидродинамический (полный) напор

(высота).

h_п = h_дл + h_мест = H₁ – H₂ – потеря напора м/у рассматриваемыми

сечениями потока.

30. Уравнения Бернулли для потока реальной жидкости.

При переходе от элементар. струйки идеал. жид-сти к потоку

реальной (вязкой) жид-сти, имеющему конечные размеры и

ограниченному стенками, необх-мо учесть неравномер-сть

распред-нияя ск-стей по сечению, а также потери энергии (на-

нора). То и другое является следствием вязкости жидкости.

При движ-ии вязкой жид-сти вдоль твердой стенки, напр. в

трубе, происходит торможение потока вследствие влияния

вязкости, а также из-за действия сил молекулярного сцепления

между жид-тью и стенкой. Поэтому наибольш. значения ск-сть

достигает в центральн. части потока, а по мере приближения к

стенке она умень-ся практически до нуля. Получается распред-е

ск-тей, подобное тому, ко­торое показано на рис.

Неравномерное распред-е

ск-стей означает сколь­же-

ние (сдвиг) одних слоев или

частей жид-сти по другим,

вследствие чего возникают

касательн. напр-ния

(напр-ния трения). Кроме того,

движ-е вязкой жид-сти часто

сопровождается

вращением частиц, вихреобразованием и перемешиванием. Все

это требует затраты энергии, поэтому удель­ная энергия

движущейся вязкой жид-сти не остается постоянной, как в

случае идеал. жид-сти, а постепенно расходуется на преод-ние

сопрот-ний и, след-но, умень-ся вдоль потока.

Из-за неравномерного распред-я ск-стей приходится вво­дить в

рассмотрение среднюю по сечению ск-сть ν_ср, а также среднее

значение удел. энергии жид-сти в данном сечении.

31. Определение расхода жидкости с использованием трубы Вентури.

Расходомер Вентури относится к дроссельным расходомерам и предст. собой устр-во, устанавливаемое в труб-дах и осуществляющее сужение потока – дросселирование. Расх-р сост. из 2-х участков – плавно суживающегося (сопла) и постеп. расшир-ся (диффузора). Скорость потока в суж-ся месте возрастает, а давл. падает. Возникает разность (перепад) давлений, кот. измер-ся двумя пьезометрами или дифференциальными U-образными маном-ми и опред. образом связана с расходом.

Допустим в сеч 1-1 ск-ть потока равна ₁, давл. р₁, площ. сеч. S₁, а в сеч. 2-2 (самое узкое место) соотв-но ₂, р₂, S₂. Разность показаний пьез-ров в этих сеч-х Н. Ур-я Бернулли и расхода для сеч-й 1-1 и 2-2: p₁/g+₁²/2g=p₂/g+₂²/2g+h_M; ₁S₁=₂S₂, где h_M – потеря напора м/ду сеч-ми 1-1 и 2-2. Учитывая, что и (р₁-р₂)/g=Н, найдем из сист. ур-й: , отсюда объемный расход или , где С=const для данного расходомера. Зная С и показания манометра, мож. найти расход в труб-де для люб. момента времени по послед. ф-ле. Константу С мож. опред-ть теор-ки, а точнее – экспер-но, т.е. в результате градуирования расходомера.

34. Характеристики турбулентного режима движения жидкости при установившемся течении в круглом трубороводе.

В общ. виде турб. поток сост. из 3-х слоев(зон):

ламинар. (Л.) слой (толщ. сост. доли мм);

переход. слой (как Л., так и турб.); ядро

турб. (Т.) режима.

Ск-ть в ядре практич. пост.. Ск-ть жид-ти

в Л. слое: _Л=0_MAX. Ср. ск-ть по сеч-ю трубопровода:

=(0,751)_МАХ. Потери напора по длине трубопровода (ф-ла

Вейсбаха-Дарси): .  (коэф-т гидродинам.

потерь) для Т. потока завис. от Re и шерох-ти. Под шерох-тью

 понимать высоту и форму выступов на стенках

трубопровода. Разл. гладкие и шерох-е трубы. Глад. трубы –

если толщ. Л. слоя (_Л) > выступов на стенке трубопровода (K).

Шерох-е трубы –если _Л<K. В

глад. трубах выступы погружены

в Л. слой, вследствии чего

отсутсвуют вихри, жид-ть

плавно обтекает выступы. Потери м. б. определены с допущ-м

как при Л. режиме. При шерох-х трубах потери обуславл-ся

вихреобразов-м. Потери эн-ии при Т. режиме завис. от шерох-

ти, диаметра трубопровода, вяз-ти и т.д. Одна и та же шерох-ть

м. несказаться в трубопроводе больш. диаметра и играть

значит. роль в трубопроводе мал. диаметра. Поэтому ввод.

понятие относ. шерох-ти =К/r; =K/d.

35. Режимы движения жидкости.

Возможны 2 разл. по своему хар-ру режима движ-я жид-ти:

ламинарный (ЛР) и турбулентный (ТР). При ЛР жид-ть движ-ся

слоями без попереч. перемеш-я, причем пульсации ск-ти и

давл-я отсутсвуют. При ТР слоистость наруш-ся, движ-е жид-ти

сопровождается перемеш-м и пульсациями ск-ти и давл-я.

Критерием для опред-я режима движ-я явл-ся безразмерное

число Рейнольдса. Re=d/; -сред. ск-ть жид-ти; d-диаметр

трубы; -кинем. вязкость жид-ти. ЛР: Re<Re_КР; ТР: Re>Re_КР .

Re_НИЖН. 2320 –ЛТ; Re_ВЕРХН.13800 –установившийся ТР.

v

36. Характеристики ламинарного режима движения жид-ти при установившемся течении в круглом трубопроводе.

Возьмем горизонтальную трубу.

; z₁=z₂=0; ₁=₂; ₁=₂; . Разность высот на

горизонт. уч-ке трубопровода пост.

диаметра дает нам потерю потенц.

энергии на разных уч-ках .

Сост. ур-ие равномерного движ-я в

выделеном стержне жид-ти:

(P₁-P₂)r²-2rl=0, где  -направл-е трения. =(P₁-P₂)r²/(2rl)=

=P_трr/(2l) (1). r. r=0  =0; r=r₀  =_max=P_трr/(2l). Направл-е

трения измен-ся по линейн. з-ну до _max.

Согласно з-ну Ньютона: =-dU/dr (2); (1)=(2);

. Интегрируем:

, U_r –местная ск-ть жид-ти, находящаяся на расст-и r от оси трубы. Приравнив-м выр-ние U=0 и опр-м знач-е постоян. C, при этом изменяя r от 0 до r. C=P_трr₀²/(4l) U_r= P_тр(r₀²-r²)/(4l) (3). При r=0 U_r=U_rmax.

z + P/γ + ν² / 2g = H ≠ const – полная удельная механич. энергия

движущейся жид-сти;

h_п = h_дл + h_мест = H₁ – H₂ – потеря полной удел. энергии по длине

струйки м/у сечениями.

h_дл – потери энергии на трение по длине;

h_мест – местные потери энергии.

Гидравлич. уклон – уменьшение значения полн. удел. энергии

жидк-сти вдоль струйки, отнесенное к единице его длины. Он

присутств. только в вязкой жид-сти и всегда направлен в

сторону движ-я, т.к. потеря энергии по длине неуклонно

возрастает.

Пьезометрич. уклон – изменение удел. потенц. энергии жид-

сти, отнесенное к единице длины. Он также связан с потерей

энергии и направлен в сторону движ-я. Но если живые сечения

струйки по течению увелич-ся в рез-те перехода кинетич.

энергии в потенц-ную, то пьезометрич. уклон могут иметь

напр-е, обратное движ-ю.

z + P/γ + ν² / 2g = H ≠ const – полная удельная механич. энергия

движущейся жид-сти;

h_п = h_дл + h_мест = H₁ – H₂ – потеря полной удел. энергии по длине

струйки м/у сечениями.

h_дл – потери энергии на трение по длине;

h_мест – местные потери энергии.

Гидравлич. уклон – уменьшение значения полн. удел. энергии

жидк-сти вдоль струйки, отнесенное к единице его длины. Он

присутств. только в вязкой жид-сти и всегда направлен в

сторону движ-я, т.к. потеря энергии по длине неуклонно

возрастает.

Пьезометрич. уклон – изменение удел. потенц. энергии жид-

сти, отнесенное к единице длины. Он также связан с потерей

энергии и направлен в сторону движ-я. Но если живые сечения

струйки по течению увелич-ся в рез-те перехода кинетич.

энергии в потенц-ную, то пьезометрич. уклон могут иметь

напр-е, обратное движ-ю.

z + P/γ + ν² / 2g = H = const – полная удельная механич. энергия

движущейся жид-сти; след-но энергетич. смысл закл. в

постоянстве вдоль струйки полной удельной энергии жид-сти,

т.о. ур-ние Бернулли выр-ет з-н сохр-я механич. энергии в

идеал. жид-сти.

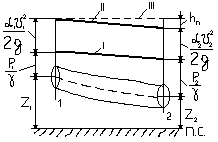
Прежде чем приступить к рассмотрению ур-ния Бернулли для

потока вязкой жид-сти, сделаем след. допущ-е: будем считать,

что в пределах рассматр-х попереч. сечений по­тока справедлив

основн. з-н гидростатики, т.е. гидростатич. напор в пределах

сечения есть вели­чина, одинаковая для всех точек данного

сечения: z + P/ (ρg) = const, т. е. предполагаем, что при

движении жид-сти отдельн. струйки оказывают одна на другую

в поперечном направ-нии такое же давление, как слои жид-сти

в неподвижном состоянии. Это соот­в-ет действит-сти и м/б

доказано теоретически в том случае, когда течение в данных

попереч. сечениях явл-ся параллельноструйным. Поэтому

именно такие (или близкие к ним) попереч. сечения и будем

рассматривать.

z₁ + P₁/γ + α₁ν_ср1² / 2g = z₂ + P₂/γ + α₂ν_ср2² / 2g + h_п

Ур-ние Бернулли для потока реальной жид-сти явл-ся ур-

нием баланса энергии в потоке жид-сти с учетом потерь.

α – коэф-т Кориолиса, кот.

харак-ет неравномерность

распред-я местных скоростей

по живому сечению. В связи с

этим вводится понятие средн.

ск-сти потока – это ск-сть, с кот.

должны были бы двигаться все

частицы(или струйки) жид-сти

через данное живое сечение, чтобы

расход всего потока был бы равен расходу, соответствующему

действительным ск-стям этих частиц (или струек). Значение α

зависит от вязкости, ск-сти движ-я жид-сти, шерох-сти стенок

трубо-да, режимов движ-я жид-сти (α=1 – для движ-я идеал.

жид-сти, 1<α<2 – для турбул. режима, α=2 – для ламинар.)

h_дл – потери напора на трение по длине;

h_мест – местные потери напора.

Энергетич. смысл

z – удельная (отнесенная к единице массы) потенц. энергия

положения жид-сти.

P/γ – удельная потенц. энергия давл-я.

z + P/γ – удельная потенц. энергия (условно).

αν_ср² / 2g – среднее значение удельной кинетич. энергии.

z + P/γ + αν_ср² / 2g = H ≠ const – полная удельная механич.

энергия движущейся жид-сти;

h_п = h_дл + h_мест = H₁ – H₂ – потеря полной удел. энергии,

затрачиваемой на преодоление сопрот-я движ-ю жид-сти м/у

сечениями потока и переходящая в тепловую энергию.

h_дл – потери энергии на трение по длине;

h_мест – местные потери энергии.

Т.о. ур-ние Бернулли явл-ся ур-нием баланса энергии в потоке

жид-сти с учетом потерь.

Гидравлич. уклон – уменьшение значения полн. удел. энергии

жидк-сти вдоль струйки, отнесенное к единице его длины.

Пьезометрич. уклон – изменение удел. потенц. энергии жид-

сти, отнесенное к единице длины. Он также связан с потерей

энергии и направлен в сторону движ-я. Но если живые сечения

струйки по течению увелич-ся в рез-те перехода кинетич.

энергии в потенц-ную, то пьезометрич. уклон могут иметь

напр-е, обратное движ-ю.

Чем >r трубы, тем > U_r. При r=r₀ U_r=0.

dQ= P_тр(r₀²-r²)rdr/(2l). Для получ-я полного

расхода необх. интегрировать от r=0 до r=r₀.

Q=P_трr₀⁴/(8l) (5).

Ф-ла Пуазейля:Q=gid₀⁴/(128) (6), где

i=₀/(gR_Г); ₀ –касат. напряж-е в р-не стенки трубопровода.

Q=d³₀/(32) (6’).

Опр-м ср. ск-ть движ-я жид-ти

по горизонт. трубопроводу:

=Q/(r₀²)=P_трr₀²/(8l) .  =U_rmax/2.

h=P_тр/=8l/(r₀²) (7); =; =g;

r₀=d/2;

h=8l4/(d²g)=|2/(2)|=(64/(d))(l/d)(²/(2g)).

h=l²/(d2g) –ф-ла Весбаха-Дарси (8), где

=64/Re –коэф-т гидродинам. потерь;

i_Г=h/l=l/d=²/(2g) –гидравлич. уклон.

Связь м/ду Н и Q получается параболической, а если по оси абсцисс откладывать расход во второй степени, то график будет предст. собой прямую. Очень часто вместо пары пьезометров для измерения перепала давления в расх-ре применяют дифференциальный ртутный манометр. Учитывая, что над ртутью в трубках находится та же ж-ть плотностью , можно записать: H=h(_рт-)/.

Ф-ла справедлива для всех дроссельных расх-ров.

1-2 –зона Л. потока. Re=1000-2300.  завис. только от Re и не

завис. от . Знач-е  опред. по ф-ле Пуазейля: =64/Re. Потери

эн-и пропорц. ск-ти в 1-ой степени: h=32(/)(l/D²).

4-5 –Т. режим теч-я в глад. трубах.  не завис. от  и опр-ся по

ф-ле Блазиуса: =0,3164/⁴Re. 2-3 и выше (обл-ть С) –переход.

зона от Л. к Т.. Обл-ть D (м/д лин. 5-4 и AB) –это переход. зона

от гидравл. глад. труб к шерох-м. В этой зоне с увел-м Re

уменьш-ся Л. слой =f(Re,). Обл-ть E –Л. слой исчезает,

полностью открывая шерох-ть. =f().

Опр-е  труб с естествен. шерох-тью для обл-тей D и E

затруднено тем обст-вом, что шерох-ть не м. б. объяснена лишь

вел-ной выступов К, поэтому ввод. понятие эквив. абс. шерох-

ти k_Э. Для опр-я  рекоменд. универс. ф-ла А.Д.Альтшуля: . При мал. Re (<10d/k_Э) ф-ла Альтшуля

переходит в ф-лу Блазиуса для глад. труб, а при больш. Re

(>500d/k_Э) обращ. в ф-лу Шифринсона для шерох. труб: .