
ЛР4_Термометр_сопротивления
.pdf
Исследование статических и динамических характеристик термометра сопротивления.
1.Цель работы:
1.1Ознакомится с принципом действия термометра сопротивления.
1.2Экспериментально получить статическую и динамическую характеристики термометра сопротивления.
1.3Определить математическую модель термометра сопротивления.
2.Теоретическая часть.
Измерение температуры термометром сопротивления основано на свойстве металлов изменять своё электрическое сопротивление с изменением температуры.
R = f (T )
где R – сопротивление термометра;
T – температура измеряемой среды.
К металлическим проводникам термометра сопротивления предъявляют ряд требований, основными из которых являются стабильность градуировочной характеристики, а также её воспроизводимость, обеспечивающая взаимозаменяемость изготовляемых термометров сопротивления. К числу не основных, но желательных требований относятся: линейность функции
R = f (T ) , по возможности высокое значение температурного коэффициента электрического сопротивления, большое удельное сопротивление. Исследованиями установлено, что чем чище металл, тем в большей степени он отвечает указанным требованиям.
Наиболее полно этим требованиям удовлетворяют платина и медь. Платиновые термометры (ТСП) используются для измерения
температуры от минус 260 до +1100оС. Медные термометры сопротивления
(ТСМ) – от минус 50 до +200 оС.
Конструктивно термометр сопротивления это – тонкая проволока или лента из платины или меди двойным слоем намотанная на каркас из керамики, слюды, кварца, стекла или пластмассы. Двойная намотка необходима для исключения индуктивного сопротивления. После намотки каркас вместе с проволокой покрывают слюдой. Каркас для защиты от повреждений помещают в тонкостенную гильзу.
Для измерения температуры термометр сопротивления помещают в измеряемую среду и по изменению сопротивления нагретого термометра определяют температуру среды, в которой он находится.
Термометр сопротивления (ТС) можно представить следующей структурной схемой:
Θсреды |
ТС |
R |
В данной работе исследуются статическая и динамическая характеристика термометра сопротивления.
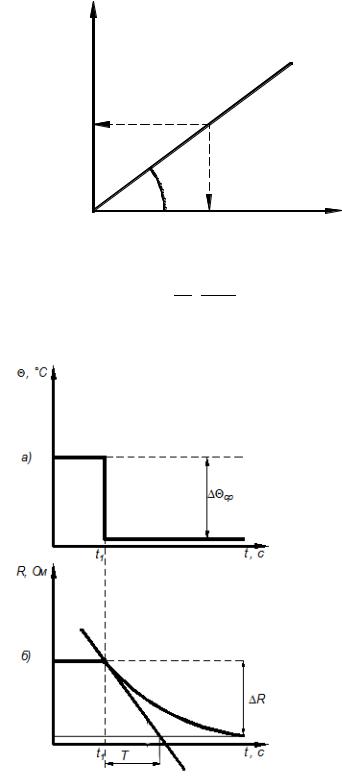
Статической характеристикой термометра сопротивления называется
|
|
|
|
|
|
зависимость сопротивления R от температуры измеряемой среды Θ среды |
в |
||||
равновесных состояниях. |
|
||||
|
|
|
|
R = f ( Θ среды |
) |
R, Ом
R0 |
0 |
|
|
tgα |
|
|
Θср,0 |
Θср,°C |
(1)
Статическая
характеристика
термометра
сопротивления изображена на рис 1.
Рис.1
Динамической характеристикой называется изменение сопротивления R во времени t при скачкообразном изменении температуры измеряемой среды
Θ среды .
R = f ( Θ среды , t )
(2)
Динамическая характеристика термометра сопротивления приведена на рис.2.
а) скачкообразное изменение температуры среды.
б) изменение сопротивления R, соответствующее данному изменению температуры.
Рис. 2
Математическая модель термометра сопротивления описывается дифференциальным уравнением:
T |
dR |
+ R = K × DQ среды |
(3) |
|
dT
где T – постоянная времени, с;
К – коэффициент усиления, Ом/ оС;
Θсреды – скачок температуры, оС;
Решение уравнения (3) представляет собой экспоненту, и для случая убывающей экспоненты имеет вид (рис.2):
|
R = K × DQсреды × e− |
t |
(4) |
|||||||
|
T |
|
||||||||
где t – время, с; |
|
|
|
|
|
|
|
|
|
|
Коэффициенты дифференциального уравнения (3) определяются по |
|
|||||||||
графикам рис.1 и рис.2. Коэффициент усиления K, можно определить по |
|
|||||||||
статической характеристике рис.1, как tgα. |
|
|
|
|
|
|
|
|||
tgα = |
|
Ro |
, |
Ом |
|
|||||
Θ |
|
|
|
|
|
|
||||
|
о |
|
|
|||||||
|
среды |
|
|
С |
|
|||||
По динамической характеристике рис.2 коэффициент усиления
определяется по формуле:
D R = K × DQ среды
Постоянная времени T определяется по динамической характеристике рис.2, как проекция касательной, проведенной к любой точке экспоненты на ось времени. Из свойств экспоненты известно, что эта величина постоянная.
3. Описание лабораторного стенда.
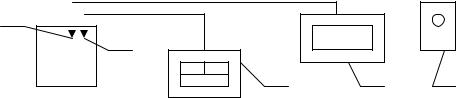
На рис.3 представлена схема лабораторного стенда, для исследования термометра сопротивления.
2
1 |
| | | | | | | | | | |
П
3 |
4 |
5 |
Условным объектом является печь П, в которой с помощью термометра сопротивления 1 измеряется температура. Данная температура фиксируется прибором 3. Омметр 4 в комплекте с термометром сопротивления 2 показывает изменение сопротивления соответствующее данному изменению температуры в печи. Изменение температуры в печи осуществляется путём её включения тумблером 5.

4. Порядок проведения работы.
4.1. Экспериментальное определение статической характеристики. 4.1.1. Подготовить таблицу 1
|
|
|
таблица 1 |
Статическая характеристика |
Динамическая характеристика |
||
Θ среды , оС |
R, Ом |
Время, с |
R, Ом |
1 |
2 |
3 |
4 |
|
|
|
|
4.1.2.Включить питание приборов. Включить нагрев печи тумблером 5.
4.1.3.Через каждые 5 оС (до температуры 100 оС) снимать показания температуры с прибора 3 и соответствующие ей показания сопротивления, с прибора 4. Данные записать в таблицу 1, графы 1 и 2.
4.2. Экспериментальное определение динамической характеристики. 4.2.1. Извлечь исследуемый термометр сопротивления 2 из печи и положить его на верхнюю панель стенда. Этим будет скачкообразно изменён
входной сигнал температуры от Θ мах =100 оС до комнатного Θ среды
4.2.2.Отключить нагрев печи тумблером 5.
4.2.3.Начиная со значения сопротивления, соответствующее Θ мах =100оС снимать показания прибора 4 через каждые 30 сек.
Данные заносить в таблицу 1, графы 3 и 4.
Показания сопротивления с прибора 4 снимать до значения
сопротивления, соответствующее температуре – Θ среды т.е. все данные по изменению сопротивления определяются скачком температуры от Θ мах =100оС
до Θ среды .
4.3. Оформление результатов эксперимента.
4.3.1. Построить статическую характеристику термометра сопротивления
R= f ( Θ среды )
4.3.2.Построить динамическую характеристику термометра
сопротивления R = f ( Θ среды , t ) .
Для этого построить динамическую характеристику по входу термометра сопротивления, т.е. Θ среды = f (t ) и соответствующее ей изменение сопротивления R = f ( t ) (см. рис.2).
4.3.3. По полученным характеристикам определить коэффициент усиления K, постоянную времени T и величину скачка ΔΘ среды .
4.3.4. Полученные коэффициенты подставить в уравнение (3) и в его решение – уравнение (4).
5. Содержание отчёта.
5.1.Цель работы.
5.2.Краткая теоретическая часть (математическая модель термометра сопротивления в общем виде, уравнение (3), (4); графики с рис.1 и 2).
5.3.Таблица 1.
5.4.Графики статической и динамической характеристик термометра сопротивления.
5.5.Определение коэффициентов математической модели термометра сопротивления.
5.6.Математическая модель термометра сопротивления с полученными коэффициентами и её решение.
Контрольные вопросы.
1.Принцип действия термометра сопротивления.
2.Определение статической и динамической характеристик термометра сопротивления.
3.Математическая модель термометра сопротивления.
4.Определение коэффициентов математической модели.
Приложение 1.
Статическая характеристика - зависимость сопротивления от температуры, в
установившихся условиях / статика /. Зависимость прямопропорциональная и имеет вид прямой линии на графике. Наклон прямой характеризует чувствительность прибора и определяется как коэффициент K = d R / d T.
Динамическая характеристика - зависимость выходного сигнала от времени при скачкообразном изменении входного сигнала на входе. На графике обычно это кривая линия в виде экспоненты, которая с течением времени стремится к значению, соответствующему исходному состоянию прибора. /динамика/. Характеристика состоит из двух графиков.
Первый график - скачок температуры во времени Второй график - рисуется под первым с соблюдением проекций основных точек
временых осей – реакция на скачок для выходного сигнала прибора.
Статическая и динамическая характеристика взаимосвязаны, и от статической зависит динамическая. Определяется динамическая характеристика постоянной времени T (сек). Если взять произвольную точку на экспоненте и провести через нее касательную, то касательная пересечет воображаемую прямую, к которой стремится экспонента. Время отсчета Т берется от проекции взятой точки касания до точки пересечения касательной с этой прямой. Так графически находится T.
Cтатическая характеристика определяется коэффициентом усиления К (mv/ C) . Графически - это отношение приращения R к приращению температуры. Коэффициент К или чувствительность прибора можно определить и по динамическим характеристикам, где приращение напряжения определено экспонентой, а приращение температуры определено скачком.
