1. 

Источник ЭДС – электротехническое устройство, преобразующее любой вид энергии в электрическую.

Проводник – вещество, обладающее большим количеством свободных носителей зарядов.

Сопротивление проводника – физическая величина, характеризующая свойство вещества препятствовать через него электрического тока.

Ветвь – заключённый между двумя узлами участок электрической цепи, по которому течёт один и тот же ток.

Узел – точка соединения трёх и более ветвей.

Контур – замкнутый участок электрической цепи, при обходе которого ни один узел и ни одна ветвь не повторяется.

2. Электрическая схема – любое графическое отображение реальной электрической цепи с помощью условных обозначений.

Последовательное соединение Параллельное соединение

Смешанное сопротивление

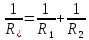или

U=U₃+U_equiv U_equiv=U₁+U₂

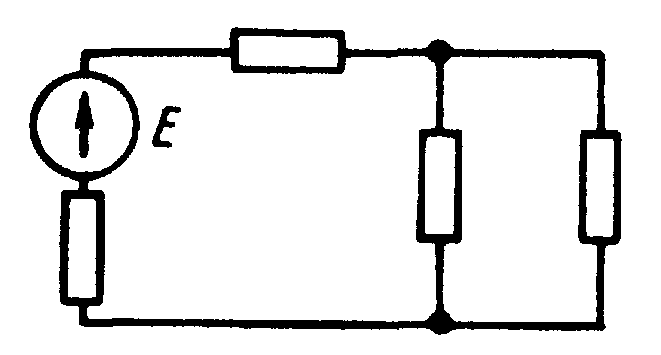
3. Ток в цепи можно определить по закону Ома (здесь и во всех последующих формулах сопротивлением соединительных проводов будем пренебрегать):

, (1)

где Е – ЭДС источника – постоянная величина, независящая от режима работы источника; R_ВН - внутреннее сопротивление источника – так же постоянная величина;

R_ПР – сопротивление приемника (нагрузки).

Перепишем уравнение (1) в следующем виде:

Е = R_ВН ∙I + R_ПР ∙I = U_ВН + U, (2)

где U_ВН = R_ВН ∙I – падение напряжения на внутреннем сопротивлении источника; а U = U_ПР = R_ПР ∙I – напряжение на зажимах источника ЭДС равное напряжению на приемнике.

Учитывая выражение (2) найдем напряжение на зажимах источника ЭДС:

U = Е – R_ВН ∙I = Е – U_ВН,

ВАХ реального источника ЭДС

Зависимость между напряжением U и током I, протекающим через источник ЭДС, представленная выражением (3), называется внешней характеристикой источника (вольт-амперной характеристикой). Внешняя характеристика источника U(I) полностью определяет свойства этого источника и для большинства реальных источников эта характеристика может быть представлена прямой линией.

3

2

1

U, [В]

U_н

U_х.х.=Е

U_С=E/2

0 I_н I_c=I_к.з./2 I_к.з. I, [A]

Из всех возможных режимов работы источника ЭДС отметим четыре наиболее важные (рис.12):

Точка 1 – холостой ход,

Точка 2 – номинальный режим,

Точка 3 – согласованный режим,

Точка 4 – короткое замыкание.

Проанализируем каждый из перечисленных выше режимов работы источника ЭДС.

Режим холостого хода (т.1) – это режим, при котором сопротивление приемника стремится к бесконечности (R_ПР = ∞) - на практике это соответствует разрыву электрической цепи, следовательно, ток холостого хода равен нулю (I_Х =0).

Из опыта холостого хода можно определить ЭДС Е показаниям вольтметра, подключив его непосредственно к разомкнутым зажимам источника ЭДС.

Номинальный режим (т.2) источника характеризуется тем, что напряжение, ток и мощность его соответствуют тем значениям, на которые он рассчитан заводами-изготовителями. При этом гарантируются наилучшие условия работы источника ЭДС (экономичность, долговечность и др.). Величины, определяющие номинальный режим, обычно указывают в паспорте, каталоге или на щитке, прикрепленном к устройству.

Согласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность Р_MAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника R_ПР равным внутреннему сопротивлению источника R_ВН, то есть R_ПР = R_ВН.

Режим короткого замыкания (т.4) характеризуется тем, что сопротивление приемника становится равным нулю R_ПР = 0. Как правило, на практике это связано с перемыканием приемника электрической энергии проводником с очень малым сопротивлением (R_ПРОВОД = 0) – так называемое промышленное короткое замыкание, зачастую вызванное неправильной эксплуатацией электротехнических устройств, как например, электрические двигатели, трансформаторы, бытовая техника и т.д.

Поменяем оси координат:

tgα пропорционален R_вн

ВАХ идеального источника ЭДС.

Если у некоторого источника R_вн=0, то tgα=0. Получаем идеализированный источник ЭДС, который характеризуется постоянным напряжением на зажимах, не зависящим от силы тока и равным Е и внутреннее сопротивление которого равно 0.

ВАХ идеального источника тока

Если увеличивать до бесконечности ЭДС и внутреннее сопротивление, то угол α стремится к 90^о. Такой источник питания называется источником тока. Это идеализированный источник питания, который создаёт то J=I, не зависящий от сопротивления нагрузки, к которой он присоединён, а его ЭДС и внутреннее сопротивление равны бесконечности.

Расчётные эквиваленты:

Источник ЭДС. Стрелка указывает направление возрастания потенциала внутри источника. R_вн=R реального источника.

Источник тока. Создаёт ток J и параллельно с ним включено внутреннее сопротивление R_в(стрелка указывает положительное направление тока источника).

Замечания:

1. Источники ЭДС и тока – идеализированные источники, физически осуществить которые, строго говоря, невозможно;

2. Схемы подключения источников эквивалентны в отношении энергии, выделяющейся на нагрузке R, и не эквивалентны в отношении энергии, выделяющейся на внутреннем сопротивлении;

3. Идеальный источник ЭДС без последовательно соединенного с ним R_н нельзя заменить идеальным источником тока.

4. 

Закон Ома для участка цепи: сила тока, протекающего по участку цепи, прямо пропорциональна напряжению на данном участке и обратно пропорциональна сопротивлению на нём.

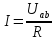
Пример.

U=9В.

Решение: I₁=9/(6+7)=0,69 А

I₂=9/8=1,125 A

I₃=9/9=1 A

I=I₁+I₂+I₃=2,815 A

5. Закон Ома для участка цепи, содержащего источник ЭДС.

На участке цепи, содержащем источники ЭДС сила тока прямо пропорциональна сумме напряжения на данном участке с суммой ЭДС источников данного участка и обратно пропорциональна сопротивлению на данном участке.

«+E» - при совпадении направлений тока на участке и стрелки ЭДС

«-E» - при несовпадении направлений тока на участке и стрелки источника

Пример:

U=9В

Решение:

I₁=(9+7)/6=2,67 А

I₂=9/8=1,125 A

I₃=9/9=1 A

I=I₁+I₂+I₃=4,795А

6. Первый и второй законы Кирхгофа (трактовка законов).

1) алгебраическая сумма токов в любом узле равна 0.

2) в замкнутом контуре алгебраическая сумма падений напряжений на каждом участве равна алгебраической сумме ЭДС, действующих в этом контуре.

Метод решения задач.

- общее число уравнений системы N равно числу ветвей N_в минус число ветвей, содержащих источники тока:

N=N_в-N_J

• Количество уравнений по первому закону Кирхгофа N₁ равно числу узлов N_у минус 1:

N₁=N_у-1

- Количество уравнений по второму закону Кирхгофа:

N₂=N-N₁=N_в-N_J-N₁

1. Перед тем, как составить уравнение нужно произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме, выбрать положительное направление обхода контура для составления уравнения по II закону Кирхгофа.

2. С целью единообразия рекомендуется для всех контуров положительное направление обхода выбирать одинаковым.

3. При записи линейно независимых уравнений по второму закону стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону(достаточное, но не необходимое условие).

4. Алгоритм составления системы уравнений по законам Кирхгофа:

- определить число узлов и ветвей N_у и N_в;

- определить число уравнений по первому и второму закону Кирхгофа N₁ и N₂;

- для всех узлов, кроме одного, выбранного произвольно составляем уравнения по первому закону;

- составляем уравнения по второму закону, включая в правую часть уравнения ЭДС, действующие в контуре, а в левую падения напряжения на резисторах. Примечание: Знак ЭДС выбирают положительным, если направление её действия совпадает с направлением обхода независимо от направления тока ветви; а знак падения напряжения на резисторе принимается положительным, если направление тока через него совпадает с направлением обхода контура.

Пример:

; ;;;

;;;;

;

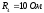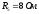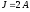Произвольно выбираем направление тока в цепях.

Первый закон Кирхгофа:

Узел :или;

Узел :или;

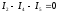Узел :или;

Второй закон Кирхгофа:

;

;

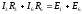Решая систему из пяти уравнений, получим следующие значения токов:

; ;;;.

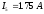7. Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы. Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.

1. Последовательное, параллельное и смешанное соединение резистивных элементов:

Последовательное соединение Параллельное соединение

Смешанное сопротивление

или

U=U₃+U_equiv U_equiv=U₁+U₂

2. Преобразование звезды в треугольник и треугольника в звезду.

Преобразование схемы типа «звезда» в схему типа «треугольник».

В узлах 1, 2, 3 и схема типа «звезда» и схема типа «треугольник» соединяются с остальной частью цепи. Часто есть необходимость преобразовать схему типа «звезда» в схему типа «треугольник» или наоборот схему типа «треугольник» в схему типа «звезда». Если преобразование выполнить так, что при одинаковых значениях потенциалов узлов, подтекающие к ним токи одинаковы, то на внешней цепи эта замена не отразится.

Переход от схемы типа «Звезда» к схеме типа «Треугольник» осуществляется по следующим формулам: ;;.

Обратный переход от схемы типа «Треугольник» к схеме типа «Звезда» осуществляется следующим образом:

;

;

;

Пример:

R_v=∞ - обрыв цепи.

R_A=0 – закорачиваем.

R_экв1=(5*6)/(5+6)=2,73 Ом

R_экв=4+2,73=6,73Ом

8. Метод двух узлов

- используется для цепей, элементы которых соединены параллельно, имеющих два узла;

- в методе за искомое принимают напряжение между двумя узлами схемы(с его помощью дальше определяются токи ветвей)

Этапы расчёта:

1. Схема имеет два узла. Потенциал точки 2 примем равным 0.

2. Составим уравнение для напряжения между узлами:

3. В знаменателе формулы – сумма проводимости параллельно включённых ветвей, а в числителе – алгебраическая сумма произведений ЭДС на проводимости ветвей, в которые эти ЭДС включены, плюс алгебраическая сумма токов от источников токов в ветвях.

4. ЭДС и J в формуле записываются со знаком «+», если они направлены к узлу 1, и со знаком «-», если направлены от узла 1.

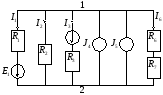
Для нашей схемы: .

Определяем токи в ветвях по закону Ома:

;

;

;

.

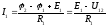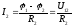После расчёта токов необходимо провести проверку по первому закону Кирхгофа.

9. Метод контурных токов.

Число уравнений, которых необходимо составить, равно числу уравнений, которых необходимо составить по второму закону Кирхгофа, или числу независимых контуров. Предполагают, что в каждом контуре течёт свой контурный ток.

В случае, когда в цепи три контурных тока, записывают систему уравнений следующим образом: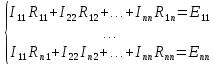. В случае, если в контур подсоединён источник тока, то в данном контуре ток известен.

Сформируем коэффициенты:

- суммы сопротивлений каждого контура.

- сопротивления общих ветвей каждого контура. Берётся со знаком «+», если контурные токи через это сопротивление текут в одну сторону, и со знаком «-», если контурные токи через него текут встречно.

–контурные токи. Направление задаётся произвольно.

–сумма ЭДС каждого контура. ЭДС берётся с «+», если совпадает с направлением контурного тока, «-», если не совпадает.

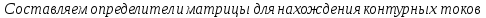
⍍R=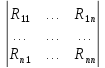– Матрица контурных сопротивлений

⍍U₁=- матрица падения напряжения на 1-м контуре.

………………………………..

⍍U_n=– матрица падения напряжения наn-ом контуре.

Далее ищем контурные токи:

, где i=1…n.

Далее ищем токи в ветвях по I закону Кирхгофа.

Пример:

; ;;

; ;;;;

;

; ;;;;- ?

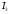Метод контурных токов:

I₃₃=J₂

R₁₁=R₅+R₆+R₄

R₂₂=R₆+R₃

R₁₂=-R₆; R₁₃=-R₄; R₂₃=-R₃

E₁₁=E₆; E₂₂=-E₁-E₆

;

Находим контурные токи. Далее находим токи в ветвях.

; ;;;

10. Электрическая мощность – это работа электрического тока в единицу времени.

В цепях постоянного тока для измерения мощности Р можно воспользоваться показаниями амперметра и вольтметра (рис. 8), тогда Р = U ∙ I, где U – напряжение на приемнике с сопротивлением R, измеренное вольтметром V, а I – ток в цепи, измеренный амперметром А.

+ А

I

U I R V

I

-

Рис. 8. Схема для измерения мощности в цепях постоянного тока с помощью амперметра А и вольтметра V.

Но более точный результат дает измерение мощности Р с помощью электродинамического ваттметра.

Для измерения активной мощности в цепях переменного тока применяют электродинамические и ферродинамические ваттметры. Класс точности электродинамических ваттметров более высокий по сравнению с ферродинамическими, поэтому электродинамические ваттметры используются для более точных измерений на низких и повышенных частотах.

Схема включения электродинамического ваттметра для измерения активной мощности Р для измерения в однофазных цепях переменного синусоидального тока приведена на рис. 9.

* 2

*

Р_W

I₁

1

1

U

I₂

Z

2

Рис. 9. Схема включения электродинамического ваттметра для измерения активной мощности в однофазных цепях переменного синусоидального тока.

Неподвижная катушка ваттметра 1-1 – это токовая обмотка прибора, она включается в цепь последовательно с сопротивлением нагрузки Z. Подвижная катушка 2-2 – это обмотка напряжения, она включается в цепь параллельно нагрузке Z. Для того чтобы включение ваттметра существенно не нарушало режима работы цепи, последовательная цепь (токовая обмотка) должна обладать относительно малым сопротивлением, а параллельная цепь (обмотка напряжения) – относительно большим. С этой целью неподвижная катушка выполнена из толстого провода, а подвижная – из тонкого.

Угол поворота стрелки, которая закреплена на подвижной катушке, пропорционален измеряемой активной мощности нагрузки:

  с·Р = с·U·I₁·cosφ = с·R₂·I₂·I₁·cosφ,

где U = R₂·I₂ – входное напряжение на подвижной обмотке 2-2; R₂ – сопротивление подвижной обмотки; I₂ – ток, протекающий в подвижной обмотке, пропорционален напряжению U контролируемой цепи и совпадает с ним по фазе, а I₁ равен току нагрузки; φ – сдвиг по фазе между вектором напряжения U и вектором тока I₁.

Шкала электродинамического ваттметра равномерная.

Направление поворота подвижной катушки зависит от направления токов I₂ и I₁ в катушках. Поэтому зажимы ваттметра, точнее один из зажимов токовой обмотки и один из зажимов обмотки напряжения, маркируются – отмечаются звездочками (*). Эти зажимы со звездочками называются генераторными, их обычно соединяют между собой и включают со стороны источника. В этом случае ток в токовой обмотке ваттметра будет равен току нагрузки I₁, а напряжение на подвижной катушке равно напряжению U. Если поменять местами зажимы одной из обмоток ваттметра, то направление вращающего момента изменится, следовательно, изменится и направление отклонения стрелки.

Для расширения пределов измерения по току следует включить параллельно токовым зажимам шунт R_Ш (при измерениях в цепях постоянного тока) или ТA, а для расширение пределов измерения по постоянному напряжению путем последовательного включения в обмотку напряжения добавочного сопротивления R_Д (при измерениях в цепях постоянного тока) или ТV (рис. 10).

U_ИСТ

R_Ш

к нагрузке U_НАГР

*

Р_W

*

R_Д

Рис. 10. Схема включения шунта R_Ш и добавочного сопротивления R_Д в цепь ваттметра Р_W.

11. Баланс мощностей:

Мощность, потребляемая источником равна мощности, потребляемой нагрузкой.

P_ист=P_нагр.

; ;;

; ;;;;

;

; ;;;;;

Расчёт.

; ;;

.

.

.

.

12. Рассмотрим механизм возникновения и основные соотношения, характерные для синусоидальной ЭДС. Для этого удобно использовать простейшую модель — рамку, вращающуюся с постоянной угловой скоростью ω в равномерном магнитном поле (рис. 2.1, а). Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции наводится ЭДС. Значение ЭДС пропорционально магнитной индукции В, длине проводника l и скорости перемещения проводника относительно поля vt:

е = Blvt .

Выразив скорость vt через окружающую скорость v и угол α, получим

е = Blv sin α = Еm sin α.

Угол α равен произведению угловой скорости рамки ω на время t:

α = ωt..

Таким образом, ЭДС, возникающая в рамке, будет равна

е = Ет sin α = Em sin ωt.

Рис.  2.1.   Модель,  поясняющая  возникновение синусоидальной  ЭДС (а); графики мгновенных значений ЭДС (б)

За один поворот рамки происходит полный цикл изменения ЭДС.

Если при t = 0 ЭДС е не равна нулю, то выражение ЭДС записывается в виде

е = Е_m sin (ωt + ψ),

где е - мгновенное значение ЭДС (значение ЭДС в момент времени t); Ет — амплитудное значение ЭДС (значение ЭДС в момент времени ωt + ψ = π/2), (ωt + ψ) - фаза; ψ - начальная фаза. Фаза определяет значение ЭДС в момент времени t, начальная фаза — при t = 0.

Таким образом для получения синусоидального токанеобходимо:

1. Магнитное поле;

2. Движение проводника в поле;

3. Замкнутый контур.

13. Синусоидальный ток – переменный ток, изменяющийся во времени по синусоидальному закону.

Переменный ток – ток изменяющийся по величине и направлению во времени с определённой частотой.

Мгновенное значение синусоидального тока – значение в конкретный момент времени.

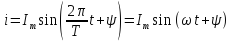
Где

I_m – амплитудное значение тока – наибольшее значение тока за период.

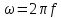- угловая частота

- частота – число колебаний в единицу времени

- период – время одного колебания.

- фаза, которая характеризует состояние колебания в момент времени.

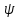- начальная фаза.

Среднее значение синусоидального тока – среднее значение тока за полупериод.

Действующее значение(среднеквадратичное) синусоидального тока – значение тока, при котором действие переменного тока(например тепловое) пропорционально квадрату данного значения.

.

На это значение реагируют приборы электромагнитной, электродинамической и тепловой систем.

14. Закон Ома в комплексной форме.

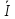–вектор тока(комплекс действующего значения тока)

- вектор напряжения(комплекс действующего значения напряжения)

- комплекс сопротивления

Пример: через зажимы двухполюсника с комплексным сопротивлением протекает синусоидальный ток Определить напряжениеu(t) на зажимах.

Решение:

;

15. Законы Кирхгофа в комплексной форме.

Первый закон Кирхгофа в символической форме:.

Второй закон Кирхгофа в символической форме: .

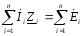Пример:

N_у=2, N_в=3,

N=N_в-N_J=3-1=2; N₁=2-1=1; N₂=2-1=1

a:

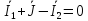
1:

16. Активное сопротивление(R) - величина, характеризующая сопротивление электрической цепи (или ее участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в др. формы (преимущественно в тепловую).

Реактивное сопротивление(X) - электрическое сопротивление, обусловленное передачейэнергиипеременным токомэлектрическомуилимагнитному полю(и обратно).(мнимое сопротивление)

Индуктивное сопротивление (X_L)– коэффициент пропорциональности между напряжением на выводах катушки, и током, протекающим через неё.

Ёмкостное сопротивление(X_C) – коэффициент пропорциональности между напряжением на выводах конденсатора и током во внешней цепи конденсатора.

Полное сопротивление(Z) – совокупность активного и реактивного сопротивления, характеризующая все потери в цепи.

X_L=ωL, где L – индуктивность, а ω – циклическая частота

X_C=1/(ωC) , где С – емкость конденсатора

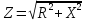
Комплекс полного сопротивления:

Можно вести расчёты, пользуясь треугольником сопротивления. Чертим отрезок, равный величине активного сопротивлении- это первый катет. Затем из конца его откладывается перпендикулярно – Х_L вверх, X_C вниз – реактивное сопротивление – второй катет. Соединяя свободные концы отрезка, получаем гипотенузу – модуль полного сопротивления. Угол между активным и полным сопротивлением показывает сдвиг фаз между током и напряжением.

Пример. Произвести расчет полного сопротивления переменного тока, в которую включена катушка, индуктивность которой L=0,096 Гн, с активным сопротивлением R=40 Ом. Напряжение на зажимах катушки 120 В. Посчитать модуль полного сопротивления по закону Ома, зная, что I=2,4 A.

Х_L=314*0,096=30 Ом

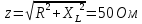
z=120/2,4=50 Ом

17. Для того, что бы построить вектор суммы нескольких векторов нужно из конца первого вектора построить второй, из конца второго третий и так далее, а затем соединить начало первого вектора с концом последнего.

Для того, что бы построить вектор разности двух векторов нужно соединить конец вычитаемого вектора с концом уменьшаемого вектора.

Диаграмма токов всегда строится по первому закону Кирхгофа, а диаграмма напряжений всегда строится по второму закону Кирхгофа.

Пример:

Дано: ,,,,,.

Требуется построить векторную диаграмму.

;

;

;

;

;

;

;

;

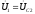18. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям(резонансной частоте), определеляемым свойствами системы.

Резонанс в электрических цепях – такой режим работы цепи, включающий в себя индуктивные и емкостные элементы, при котором её входное сопротивление(проводимость) вещественно.

В цепи, в которой включены последовательно конденсатор, катушка индуктивности и конденсатор, возможно возникновение резонанса напряжений при определённых условиях.

Условия возникновения:

1. Цепь с источником переменного напряжения;

2. Последовательное включение реактивных элементов;

3. Равенство реактивных сопротивлений или равенство падений напряжения на реактивных элементах при условии, что C и L не равны 0.

4. 

Способы достижения:

1. Изменение L при постоянных С и ω;

2. Изменение С при постоянных L и ω;

3. Изменение ω при постоянных C и L.

Изменение параметров цепи:

1. Нагрузка имеет чисто активный характер(z=R);

2. Отсутствует сдвиг фаз между напряжением и током;

3. Эквивалентная полная мощность цепи становится чисто активной(эквивалентная реактивная мощность равна 0)

4. Сила тока, протекающего в цепи в момент резонанса, будет максимальной

5. Падения напряжений на катушке и конденсаторе практически будут равны между собой

6. Идеальный резонанс напряжений эквивалентен короткому замыканию входных зажимов цепи

19. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям(резонансной частоте), определеляемым свойствами системы.

Резонанс в электрических цепях – такой режим работы цепи, включающий в себя индуктивные и емкостные элементы, при котором её входное сопротивление(проводимость) вещественно.

При параллельном соединении катушки индуктивности и конденсатора возникает резонанс токов при определённых условиях.

Условия возникновения:

1. Цепь с источником переменного напряжения;

2. Параллельное включение реактивных элементов;

3. Равенство реактивных проводимостей или равенство токов в параллельных ветвях при условии, что C и L не равны 0.

4. 

Способы достижения:

1. Изменение L при постоянных С и ω;

2. Изменение С при постоянных L и ω;

3. Изменение ω при постоянных C и L;

4. Изменение активного сопротивления в параллельных ветвях, при условии не равных 0 L и C и постоянной ω.

Изменение параметров цепи:

1. Сила тока на входе резонансного контура в момент резонанса будет минимальной

2. Токи, протекающие в параллельных ветвях практически равны между собой

3. Если считать катушку индуктивности идеальной (R_К = 0), тогда токи в катушке и конденсаторе будут равны между собой

4. Идеальный резонанс токов эквивалентен разрыву (холостому ходу) в цепи

5. в режиме резонанса токов, вектор входного напряжения U совпадает по фазе с вектором входного тока I_P = I, т.е. фазовый сдвиг между этими векторами:

_Э = _U - _I = 0

6. Эквивалентная полная мощность цепи становится чисто активной(эквивалентная реактивная мощность равна 0)