Физика теория к задачам вар №19

Физика теория к задачам.

№1

Линейная плотность электрического заряда — предел отношения электрического заряда, находящегося в элементе линии, к длине этого элемента линии, который содержит данный заряд, когда длина этого элемента стремится к нулю.

Единицей измерения является кулон на метр (Кл/м).

Dq-Бесконечно малый заряд, который соответствует бесконечно малому

элементу длины нити.

Dl Бесконечно малый элемент длины нити

Потенциал –

 скалярнаяэнергетическая характеристика

 электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда

связь между потенциалом и напряженностью электрического поля- Для установления связи между силовой характеристикой электрического поля -напряжённостью и его энергетической характеристикой – потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда 

q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда 

q: dA = - dW_п = - q d, где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат

E_x dx + E_y dy + E_z dz = -d, 

откуда 

 Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad  = -Ñ.

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала. Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен  = q / 4pe₀er.

№2

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

 Энергия конденсатора при наличии диэлектрика. Энергия поля в диэлектрике, Посмотрим, что происходит с энергией конденсатора при введении между его пластинами диэлектрика. Энергия конденсатора Е определяется соотношением  W = 1/2q(φ₁ – φ₂)

где q — заряд пластины конденсатора. Так как это выражение для W получено лишь на основании подсчета работы переноса зарядов между пластинами с данными разностями потенциалов, то оно остается в силе и при наличии между пластинами конденсатора диэлектрика. Эта формула позволяет сравнить энергию W пустого конденсатора с энергией W'такого же конденсатора, заполненного диэлектриком. Здесь надо уточнить условия, при которых идет сравнение.  Если заряды на обкладках пустого конденсатора и конденсатора с диэлектриком одинаковы, то различие в энергии обусловлено различием разностей потенциалов на обкладках обоих конденсаторов. В этом случае разность потенциалов на обкладках заполненного диэлектриком конденсатора в ε раз меньше разности потенциалов на обкладках пустого конденсатора, поэтому при этих условиях мы получаем W'/W = 1/ε, т. е, энергия конденсатора уменьшаетсяпри заполнении его диэлектриком в ε раз. Наоборот, если у пустого и заполненного диэлектриком конденсатора на обкладках поддерживаются одинаковые разности потенциалов,то, энергии будут пропорциональны свободным зарядам q на обкладках. В этом случае, как мы видели, заряд обкладок заполненного диэлектриком конденсатора в ε раз больше, чем заряд обкладок пустого конденсатора, и мы получаем W'/W = ε, т. е. энергия конденсатора возрастаетпри заполнении его диэлектриком. Увеличение энергии происходит за счет источника, поддерживающего неизменную разность потенциалов на обкладках. Из выражения для энергии конденсатора W = 1/2q(φ₁ – φ₂) легко найти плотность энергии, электростатического поля внутри диэлектрика. Для этого рассмотрим плоский конденсатор, заполненный диэлектриком, поле в котором можно считать однородным. Подставляя в выражение для энергии заряд q и разность потенциалов (φ₁ - φ₂₎, выраженные через напряженность поля, q= σS = ε₀εSE/ и (φ₁ –φ₂ )= Ed, найдем W = ε₀εE²Sd/2 

Деля последнее выражение на объем диэлектрика в конденсаторе Sd, получим для плотности энергии в диэлектрике выражение: w= ε₀εE²/2

В результате поляризации на гранях диэлектрика, обращенных к пластинам конденсатора, концы молекулярных диполей окажутся нескомпенсированными соседними диполями. Поэтому на правой грани, обращенной к отрицательной пластине конденсатора, окажется избыток положительного заряда с некоторой поверхностной плотностью ⁺ ’. На противоположной стороне диэлектрика

 ^-’ . Эти так называемые поляризационные, или связанные заряды не могут быть переданы соприкосновением другому телу без разрушения молекул диэлектрика, т.к. они обусловлены самими поляризованными молекулами. Возникновение поляризованных зарядов приводит к возникновению дополнительного электрического поля  , направленного против внешнего поля  . Результирующее электрическое поле Е внутри диэлектрика равно

Для определения  применим формулу вычисления напряженности  конденсатора

№3

На рамку действует пара сил, в результате чего она поворачивается.

1.     Направление вектора силы – правилу левой руки.

2.     F=BIlsin=ma

3.     M=Fd=BIS sin - вращающий момент

закон Ампера-

Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: 

F=B^.I^.ℓ^. sin

количественное выражение для магнитиой индукции в результате обобщения опытных данных было установлено Био и Саваром (фиг. 83). Измеряя по отклонению магнитной стрелки магнитные поля электрических токов различной величины и формы, оба ученых пришли к выводу, что всякий элемент тока создает на некотором расстоянии от себя магнитное поле, магнитная индукция которого АВ прямо пропорциональна длине А1 этого элемента, величине протекающего тока I, синусу угла а между направлением тока и радиусом-вектором, соединяющим интересующую нас точку поля с данным элементом тока, и обратно пропорциональна квадрату длины этого радиуса-вектора r:

где К — коэффициент, зависящий от магнитных свойств среды и от выбранной системы единиц.

µ- относительная магнитная проницаемость — безразмерный коэффициент, показывающий, во сколько раз магнитная проницаемость данного материала больше магнитной проницаемости пустоты. Размерность магнитной индукции можно найти по формуле

№4

Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина

В случае плоского контура с электрическим током магнитный момент вычисляется как

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим

№5 Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В Международной системе единиц (СИ):  где  — магнитная постоянная.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующаяэлектрическое поле в данной точке и численно равная отношению силы  действующей на неподвижный пробный заряд помещенный в данную точку поля, к величине этого заряда :

.

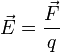ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Здесь e — диэлектрическая, m — магн. проницаемости среды, Е0 и H0 — амплитуды колебаний электрич. и магнит. полей, w=2pn — круговая частота этих колебаний, j — произвольный сдвиг фазы, k — волновой вектор, r — радиус-вектор точки; N — оператор Лапласа

(E^H^ k, H0 =O(e/m)E0).

объемная плотность энергии электрического поля равна

,

(1.1)

а магнитного поля –

,

(1.2)

где  и  – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна

В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: w_э = w_м.