 TWISTER OFFICE^ КОНСПЕКТЫ ЛЕКЦИЙ ПО ФИЗИКЕ ДИСПЕРСНЫХ СРЕДwww.rf-99-8.h1.ru

но , гдеd_zz - поляризуемость молекулы вдоль оси z.

Выражение для величины поляризации молекулы: .

Предположим, что А и В не взаимодействуют, тогда для их системы :

,.

Введем взаимодействие между двумя молекулами:

Дипольное .V_AB может выступать в роли возмущения, тогда энергия системы ,.

Обозначим m= {i, k}, n= {j, l}

Энергия взаимодействия этих молекул: .

=

dA_ii - дипольный момент молекулы А в состоянии i (невозмущенный).

DВ_kk - дипольный момент молекулы В в состоянии k.

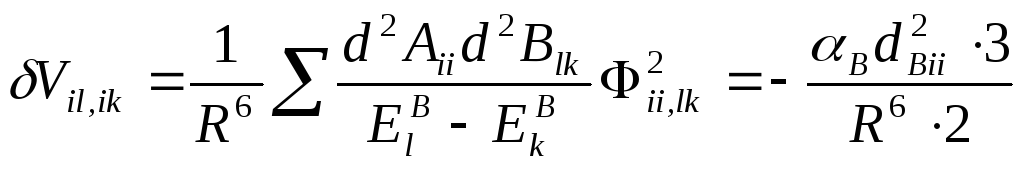
В случае если обе молекулы находились в основном состоянии (i=1, k=1):

-

- энергия взаимодействия двух молекул на достаточно большом расстоянии.

2002. Проведем термодинамическое усреднение последнего полученного выражения:

Оценка взаимодействий:



В квантовой механике рассматривается задача о взаимодействии двух молекул на расстоянии. После термодинамического усреднения получаем, что это взаимодействие состоит из трёх: ориентационное взаимодействие + поляризационное взаимодействие + дисперсионное взаимодействие.

- характерное время в течение которого молекула обладает дипольным моментом.

- Формула Лондона - приближенное выражение дисперсионных сил.

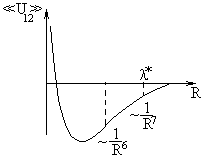Мы предполагали, что молекулы изотропны (симметричны). Если же это резко анизотропные структуры, то их взаимодействие будет зависеть от их ориентации в пространстве.

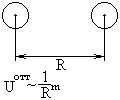
Пусть расстояние между молекулами R~2a.

Отталкивание обусловлено:

1. Электростатическое отталкивание

2. Обменные силы

3. Рост кинетической энергии (чем больше энергия, то больше отталкивание).

,m - достаточно большое.

Потенциал Ленорда-Джонса:

,m = 12, n = 6.

 ~ 0,01 эВ

d ~ 0,9R₀Å ~ 1-2 Å

Описание макроскопических свойств систем взаимодействующих молекул:

Параметры системы: V, N (10²⁷…), Т, Р. ;

средняя энергия взаимодействия: ,n - концентрация.

 (P,V,T) = 0

1. Менделеева-Клайперона: приближения от<R> |<U>| << KT

PV = NKT

2. PV_n  RT B--B:

,

МЕХАНИКО-СТАТИСТИЧЕСКИЙ ПОДХОД:

,

Если взаимодействием частиц пренебрегать:

=

=

• 

==========22.10.2002==========================

, ,

ВЫДЕЛЕНИЕ КОНФИГУРАЦИОННЫХ ИНТЕГРАЛОВ.

(*)

Как ведет себя U_ij в зависимости от r_ij и от r_ij:

-

• Функция Майера

Подставим в (*) exp как f_ij + 1  .

, тогда конфигурационный интеграл:

имеем

=

Иллюстрируя графически, заменим:

• Это групповое разложение для конфигурационного интеграла.

• 

• Если взаимодействие слабое, то 

• 

• в случае слабого взаимодействия: . Тогда будем брать только

первые члены разложения:

=

=(это сумма интегралов, но они ни чем не отличаются друг от друга, т.к. функцииf_ij зависят от r_ij одинаково:

) = (**)

(переходим от переменных кОшибка! Ошибка связи.)

= , тогда (**) будет выглядеть так:

(**) =

, (1)

, где a - размер молекулы.

/, тогдаln(1+)   ;

/ =

УРАВНЕНИЕ В-Д-В: или .

,

тогда

, но мы находили, что ;

.

Таким образом, ,- четыре объема молекулы.

ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ: ,n - концентрация.



- разложение по степеням плотности, число эмпирическое, B₁, B₂ - вириальные коэффициенты, их можно сосчитать при помощи группового

разложения.

СТАТИСТИЧЕСКАЯ МЕХАНИКА В ТЕОРИИ ЖИДКОСТЕЙ

В случае жидкости взаимодействие не слабое, расстояние между молекулами порядка их размера.

не может считаться малым, иными словами все разложения по малым параметрам в случае идеального газа теряют смысл для жидкости.

КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ:

Всистеме из N частиц

состояние i - частицы зависит от состояния j - частицы.

Вероятность i - частице оказаться в объеме dV_i:

, для идеального газа -.

Вероятность того, что i - частица находится в dV₀, а j - в то же время в dV_j:

,

g_i, g_ij - одно- и двухчастичная функция распределения.

h₁₂ =g₁₂ - 1 - ФУНКЦИЯ КОРРЕЛЯЦИИ (парная (отличается сдвигом на 1 от функции распределения). Парная функция распределения g₁₂ должна быть > 0 и может быть > 1, если она не ориентирована (по сути дела это плотность вероятности).

,

g > 0 - на этих расстояниях частицам выгодно находиться, по сравнению с идеальным случаем.

Выразить функцию корреляции через параметры системы:

- распределение Больцмана.

;

, и т. п.

По определению: ;

 , и т. п.

Предположение U_N  U_ij - пока нет.

От чего зависит g₁₂? g₁₂ = g(r₁₂).

ПРИМЕР:

Взаимодействующие шарики невзаимодействующие шарики

ФУНКЦИЯ ПАРНОЙ КОРРЕЛЯЦИИ:

интенсивность рассеивания I

в зависимости от угла рассеивания:

индикатриса

рассеивания

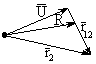
Свяжем расстояние с числом рассеивающих центров: , где_i- вектор направления поля от i - частицы, _ij - вектор направления поля от j - частицы.

,

- волновой вектор.

- волновой вектор рассеяния.

Понятно, что суммарная интенсивность состоит из: сумма интенсивности от каждого из центров (I_неког) + некая добавка (I_ког):

I = I_неког + I_ког.

Наличие второго слагаемого ответственно за структуру (связь рассеивающих центров друг с другом) системы.

Вводится величина - СТРУКТУРНЫЙ ФАКТОР РАССЕЯНИЯ: ,

Т.е. если есть корреляция, то S(q)  1,если нет - S(q) = 1.

S(q) как-то связана с g₁₂.

, где - расстояние между частицами. Эта формула - связьS(q) с h₁₂, если грамотно сделать обратное преобразование:

- так мы находим функцию корреляции.

Используем - парный характер взаимодействия.

Средн. энергия системы

=

=

можно найти .

Связанная энергия: F = - kT lnZ_N, .

В случае, если взаимодействие парное:

уравнение состояния