Лабораторной работе №134 изучение прецессии гироскопа краткая теория

В механике твердого тела рассматривается движение абсолютно твердого тела, т.е. такая система материальных точек, при любых движениях которой взаимное расстояние между ними остается неизменным. Иначе говоря, размеры и форма абсолютно твердого тела не изменяются при его движении. В природе нет абсолютно твердых тел – это физическая абстракция. Всякое тело под действием приложенных к нему сил в большей или меньшей степени деформируется, т.е. изменяет свою форму и размеры. Однако в тех случаях, когда деформация тела при его движении пренебрежимо малы, тело можно считать абсолютно твердым.

Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное.

Поступательное движение – это такое движение, при котором любая прямая, соединяющая две точки тела, остается параллельной самой себе.

Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться и вне тела. Окружности, описываемые точками вращающегося тела, располагаются в плоскостях, перпендикулярных к оси вращения.

Рассмотрим кинематику вращательного движения твердого тела.

Рис. 1

Величина элементарного перемещения точки А вращающегося твердого тела dS = АА^/ связана с угловым перемещением , совершаемым за бесконечно малый промежуток времени dt , формулой: (1)

где- радиус окружности, описываемой точкой А.

Так как - линейная скорость данной точки вращающегося тела, то

(2) где (3)

• угловая скорость, равная производной от углового перемещения от времени.

При равномерном вращении угловая скорость

(4)

т.е. равна углу поворота за единицу времени.

Размерность равна

Для полноты характеристики вращательного движения должно быть указано не только числовое значение угловой скорости, но и ориентация оси вращения и направление вращения.

Задать все эти характеристики одновременно можно, рассматривая угловую скорость как вектор.

Вектор угловой скорости направлен по оси вращения, и его направление определяется по правилу буравчика.

Если направление вращения ручки буравчика (с правовинтовой нарезкой) совпадает с направлением вращения тела, то направление поступательного движения буравчика совпадает с направлением вектора угловой скорости _. (рис. 2)

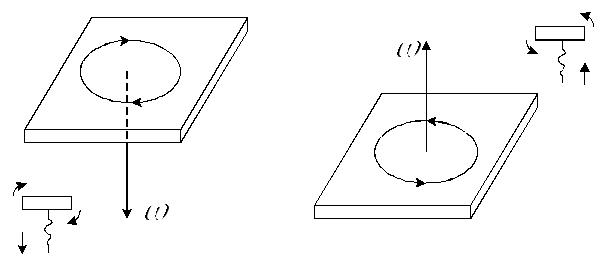
Рис. 2

Установим связь между направлениями векторов , и .

Расположение этих векторов указано на рис. 3

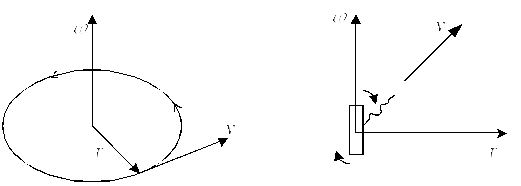
Рис. 3

Как видно, вектор перпендикулярен и к вектору , и к вектору . Направление вектора можно определить по правилу буравчика (рис. 3). Такая же связь существует между направлениями двух перемножаемых векторов и их векторного произведения. Поэтомут.е. является векторным произведением и.

Если радиус-вектор расположен в плоскости, перпендикулярной оси вращения, то модуль вектора линейной скорости равен:

(5)

При неравномерном вращении быстроту изменения угловой скорости характеризуют величиной, которую называютугловым ускорением. Вектор углового ускорения определяют как производную от угловой скорости по времени.

: .

В случае неподвижной оси, когда векторы инаправлены по оси вращения, вектор тангенциального ускорения и вектор углового ускорения связаны следующим соотношением:

Если угловая скорость возрастает по величине, то вектор углового ускорения совпадает по направлению с вектором , а векторнаправлен по касательной в ту же сторону, что и линейная скорость (рис. 4).

Ускоренное движение

Рис. 4