физикаЛБ-250

ЛАБОРАТОРНАЯ РАБОТА № 250

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА МЕТОДОМ ПЕРЕЗАРЯДКИ.

1. ЦЕЛЬ И СОДЕРЖАНИЕ РАБОТЫ:

Целью работы является ознакомление с методом измерения емкости конденсаторов способом их периодической зарядки и разрядки.

Работа состоит в измерении емкости отдельных конденсаторов и их соединений.

2. КРАТКАЯ ТЕОРИЯ РАБОТЫ.

Для зарядки разных проводников до одинакового потенциала им необходимо сообщить различные заряды q. Это свойство проводников характеризуется величиной, называемой емкостью. Емкость проводника численно равна : .

Емкость зависит от формы внешней поверхности проводника, его линейных размеров, от величины диэлектрической проницаемости окружающей среды, а также от расположения данного проводника относительно других проводников.

Система двух проводников, емкость которой не зависит от окружающих тел, называется конденсатором. Емкость конденсатора численно равна отношению заряда, помещенного на одной из обкладок конденсатора , к разности потенциалов между ними: .(1)

Простейшие измерения емкости при переменном токе производятся на основании закона Ома с помощью стрелочных приборов и являются довольно грубыми. Более распространены измерения на переменном токе с применением мостовых схем. В прецезионных измерениях емкости на переменном токе используется резонансный метод.

В данной работе применен способ определения емкости методом перезарядки.

Как следует из (1), для нахождения емкости конденсатора следует произвести измерения напряжения и заряда. Заряд может быть измерен при периодической разрядке конденсатора, с помощью простого микроамперметра по среднему разрядному току.

Допустим, что исследуемый конденсатор емкости С разряжается через микроамперметр, сопротивление которого R. Известно, что при этом сила разрядного тока убывает по экспоненциальному закону: , представленному на рисунке 1.Полный заряд конденсатора, в соответствии с определением силы тока, найдется по закону: и изобразится площадью под кривой разрядного тока.

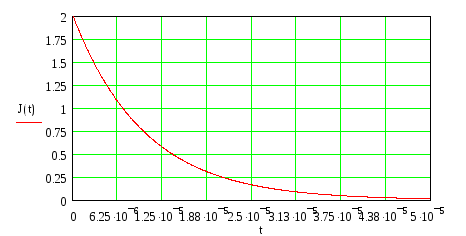
Однако микроамперметр не дает возможности снять такую кривую, так как время установления стрелки значительно больше времени разряда конденсатора.

На рисунке 2 приведена схема, позволяющая периодически заряжать и разряжать конденсатор.

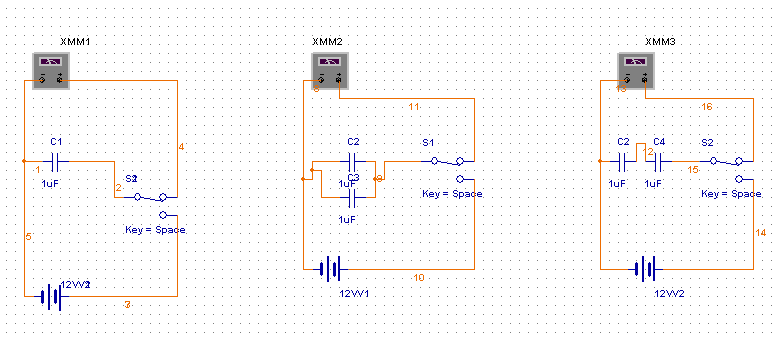
При замыкании контактов 1-2 конденсатор заряжается до напряжения источника питания, а при замыкании контактов 1-3 он полностью разряжается через микроамперметр. Если интервал между двумя последовательными разрядами конденсатора мал по сравнению с периодом собственных колебаний подвижной системы прибора, то микроамперметр будет давать некоторое постоянное отклонение, которое, как можно показать, соответствует средней силе тока J cp за время (рис.3)

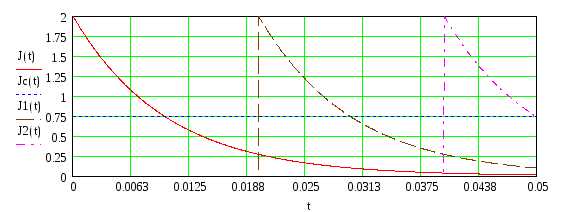
Установим соотношение между средним током J cp и зарядом конденсатора :

Если за некоторое время t конденсатор будет N раз разряжаться на микроамперметр имея при этом одинаковый заряд q , то полный заряд, прошедший через прибор за это время: Q=qN. , численно равен количеству электричества, прошедшему через микроамперметр за 1 сек., следовательно: Q=Jc*t.Отсюда: q=Jc*t/N. Обозначая число разрядов за 1 сек через f=N/t, получаем расчетную формулу для емкости конденсатора; C=q/u=Jc/U*f(2).

3. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ , НЕОБХОДИМЫЕ ДЛЯ ВЫПОЛНЕНИЯ РАБОТЫ.:

1. Источник постоянного напряжения.

2. Вольтметр.

3. Исследуемые конденсаторы.

4. Микроамперметр.

5. Автоматический переключатель.

В качестве автоматического переключателя в данной работе используется поляризованное реле, Схема показана на рисунке 4.

На подковообразном железном сердечнике сделана намагничивающая обмотка, по которой пропускается переменный ток частоты f , указанный на лимбе генератора сигналов низкой частоты. Между полюсами сердечника помещен намагниченный стержень- якорь, Если через обмотку и пропускается переменный ток, создающий переменное по величине и направлению магнитное поле, то в независимости от направления тока в обмотке якорь притягивается то к одному , то к другому из полюсов Р или К (плоская пружина, удерживающая якорь в среднем положении при этом изгибается). Таким образом, клемма 1 через якорь и контактыL и М поочередно соединяется с клеммами 2 и 3 по 50 раз в секунду. Внутреннее сопротивление источника постоянного напряжения , емкость конденсатора и сопротивление микроамперметра выбраны столь малым, что конденсатор успевает зарядиться и разрядиться полностью за время , меньшее времени, в течение которого контакты 1-2 и 1-3 замкнуты. Реле работает от переменного напряжения 24В.

4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

Собирают схему в соответствии с рисунком 5.

Включают источник постоянного напряжения и записывают показания вольтметра .Далее включают поляризованное реле и определяют по микроамперметру средний Jc разрядный ток.

По формуле (2) определяют емкость конденсатора С1 . Затем проделывают измерения емкости С1 при других значениях напряжения.

Аналогично определяют емкости других конденсаторов С2, С3 и С1, а также емкость при параллельном и последовательном соединении конденсаторов.

Результаты записывают в таблицу1 и таблицу 2.

№	U,B	J1,,мкА	J2, мкА	C1,мкФ	C2,мкФ
1
2
3
4
5
6
Среднее значение емкости

Параллельное соединение конденсаторов:

№	U,B	J,мкА	C”,мкФ
1
2
3

Последовательное соединение конденсаторов:

№	U,B	J,мкА	C”,мкФ
1
2
3

5.КОНТРОЛЬНЫЕ ВОПРОСЫ.

1.Выведите формулу для расчета емкости плоского конденсатора.

2. Как зависит емкость конденсатора от диэлектрической проницаемости среды, заполняющей пространство между его обкладками?

3. В каких единицах измеряется емкость в системах СИ и СГСЭ? Каково соотношение между этими единицами?

4. Как пишется закон Ома для амплитудных значений силы тока и напряжения в цепи переменного тока, содержащей только емкость?

5. Запишите закон изменения разности потенциалов на обкладках конденсатора при разрядке его через сопротивление.

6.ЛИТЕРАТУРА.

1. С.Г. Калашников, «ЭЛЕКТРИЧЕСТВО», изд.1964г.

2. В.А. ШТРАУФ, 2КУРС ФИЗИКИ», изд.1962г.