
- •Электрические цепи постоянного тока.
- •Энергетический баланс.
- •Принцип (метод) наложения.
- •Преобразование схемы типа «звезда» в схему типа «треугольник».
- •Метод эквивалентного генератора.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Электрические цепи однофазного синусоидального тока.
- •Конденсатор в цепи синусоидального тока.
- •Основы символического метода:
- •Активная, реактивная и полная мощности.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Трёхфазные цепи.
- •Расчёт трёхфазных цепей.
- •Активная, реактивная и полная мощности трёхфазных цепей.
- •Измерение активной мощности трёхфазной цепи.
- •Магнитные цепи.
- •Уравнения напряжений и токов трансформатора.
- •Уравнения магнитодвижущих сил и токов.
- •Изменение вторничного напряжения.
- •Потери энергии в трансформаторе.
- •PГруппы соединений трёхфазных трансформаторов.
- •Вращающееся магнитное поле.
- •Получение кругового вращающегося магнитного поля.
- •Принцип действия асинхронного двигателя.
- •Устройство асинхронного двигателя.
- •Формула для нахождения частоты вращающегося поля.
- •Эдс статора и неподвижного ротора. Режим холостого хода.
- •Эдс вращающегося ротора.
- •Устойчивая работа двигателя.
- •Влияние изменения напряжения сети.
- •Регулировка скорости вращения асинхронного двигателя.
- •Тормозные режимы.
- •Синхронный двигатель.
- •Влияние тока возбуждения на работу двигателя.
- •Пуск синхронного двигателя.
- •Выпрямление переменного напряжения.
Уравнения напряжений и токов трансформатора.
Токи
![]() и
и
![]() помимо основного магнитного потока
создают поток рассеивания. Каждый поток
рассеивания связан только с витками
собственной обмотки, и индуцирует в
ней ЭДС рассеивания. Потоки рассеивания
не участвуют в передаче энергии.
помимо основного магнитного потока
создают поток рассеивания. Каждый поток
рассеивания связан только с витками
собственной обмотки, и индуцирует в
ней ЭДС рассеивания. Потоки рассеивания
не участвуют в передаче энергии.
ЭДС рассеивания в первой в первой
обмотке можно найти по формуле:
![]() ,
ЭДС рассеивания во второй обмотке
определяется аналогично:
,
ЭДС рассеивания во второй обмотке
определяется аналогично:
![]() ,
где
,
где
![]() - индуктивность рассеивания. Тогда:
- индуктивность рассеивания. Тогда:
![]() ;
;
![]() ,
где
,
где
![]() - индуктивные сопротивления рассеивания.
- индуктивные сопротивления рассеивания.
Таким образом, в каждой обмотке трансформатора индуцируется по две ЭДС: от основного потока и от потока рассеивания.
Со стороны первичной обмотки трансформатор
является потребителем энергии,
поэтому ток в первичной обмотке
создаётся совместным действием входного
напряжения
![]() и двух ЭДС:
и двух ЭДС:
![]() ,
где
,
где
![]() - активное сопротивление первичной
обмотки. Тогда:
- активное сопротивление первичной
обмотки. Тогда:
![]() ;
;
![]() ;
;
![]() - уравнение напряжения для первичной
обмотки.
- уравнение напряжения для первичной
обмотки.
Со стороны вторичной обмотки трансформатор
является источником энергии, поэтому
ток во вторичной обмотке, замкнутой на
сопротивление
![]() ,
обусловлен действием двух ЭДС:
,
обусловлен действием двух ЭДС:
![]() ,
где
,
где
![]() - активное сопротивление вторичной
нагрузки. Тогда:
- активное сопротивление вторичной
нагрузки. Тогда:
![]() ;
;
![]() - уравнение напряжений для вторичной
обмотки.
- уравнение напряжений для вторичной
обмотки.
Уравнения магнитодвижущих сил и токов.
П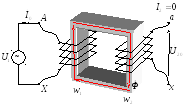 редположим,
что трансформатор работает в режиме
холостого хода, то есть к зажимам
первичной обмотки подведено напряжение
редположим,
что трансформатор работает в режиме
холостого хода, то есть к зажимам
первичной обмотки подведено напряжение
![]() ,
а вторичная обмотка разомкнута. При
этом по первичной обмотке протекает
ток
,
а вторичная обмотка разомкнута. При
этом по первичной обмотке протекает
ток
![]() ,
называемый током холостого хода, который
обычно составляет от двух до десяти
процентов от номинального тока
,
называемый током холостого хода, который
обычно составляет от двух до десяти
процентов от номинального тока
![]() .
Этим током создаётся магнитодвижущаяся
сила, которая равна произведению тока
и числа витков в первичной обмотке.
Положительное направление МДС совпадает
с движением острия правого винта, если
его вращать по направлению тока в
обмотке. МДС наводит в магпитопроводе
основной магнитный поток
.
Этим током создаётся магнитодвижущаяся
сила, которая равна произведению тока
и числа витков в первичной обмотке.
Положительное направление МДС совпадает
с движением острия правого винта, если
его вращать по направлению тока в
обмотке. МДС наводит в магпитопроводе
основной магнитный поток
![]() ,
где
,
где
![]() - магнитное сопротивление магнитопровода.
- магнитное сопротивление магнитопровода.
Е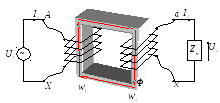 сли
вторичную обмотку замкнуть на нагрузку
сли
вторичную обмотку замкнуть на нагрузку
![]() ,
то по ней потечёт ток
,
то по ней потечёт ток
![]() .
При этом ток в первичной обмотке
увеличивается до значения
.
При этом ток в первичной обмотке
увеличивается до значения
![]() в соответствии с законом сохранения
энергии. Трансформатор отдаёт энергию
нагрузке, поэтому требуется соответствующий
приток энергии от сети. Теперь магнитный
поток
в соответствии с законом сохранения
энергии. Трансформатор отдаёт энергию
нагрузке, поэтому требуется соответствующий
приток энергии от сети. Теперь магнитный
поток
![]() создаётся совместным действием МДС
обеих обмоток.
создаётся совместным действием МДС
обеих обмоток.
Опыт и расчёт показывают, что если
первичное напряжение постоянно, то есть
![]() ,
то при изменении нагрузки от нуля (режим
холостого хода) до номинальной (номинальный
режим) максимальный магнитный поток
остаётся практически постоянным, то
есть
,
то при изменении нагрузки от нуля (режим
холостого хода) до номинальной (номинальный
режим) максимальный магнитный поток
остаётся практически постоянным, то
есть
![]() .
.
Уравнение МДС:
![]() .Тогда:
.Тогда:
![]() ;
;
![]() ;
;
![]() ,
где
,
где
![]() - ток нагрузки, приведённый к числу
витков первичной обмотки.
- ток нагрузки, приведённый к числу
витков первичной обмотки.
Уравнение токов трансформатора:
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Так как ток
![]() то можно приблизительно считать, что
то можно приблизительно считать, что
![]() ,
то есть коэффициент трансформации
приближённо можно найти по формуле:
,
то есть коэффициент трансформации
приближённо можно найти по формуле:
![]() .
.
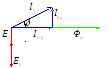
Из-за наличия потерь ток холостого хода
![]() опережает по фазе магнитный поток в
стальном сердечнике
опережает по фазе магнитный поток в
стальном сердечнике
![]() на угол
на угол
![]() ,
который называется углом магнитных
потерь.
,
который называется углом магнитных
потерь.
![]() .
.
Активная составляющая тока холостого
хода
![]() идёт на преодоление потерь в стали, а
реактивная составляющая тока холостого
хода
идёт на преодоление потерь в стали, а
реактивная составляющая тока холостого
хода
![]() идёт на создание магнитного потока в
сердечнике. Поэтому ток холостого хода
идёт на создание магнитного потока в
сердечнике. Поэтому ток холостого хода
![]() в основном является намагничивающим
током.
в основном является намагничивающим
током.
Приведение параметров вторичной обмотки и
схема замещения приведённого трансформатора.
Для электрического расчёта трансформатора
необходима электрическая схема замещения.
Трансформатор представляет собой
систему двух магнитно-связанных между
собой цепей, поэтому требуется
предварительное привидение первичной
и вторичной цепи к одному уровню
напряжений. Обычно, действительная цепь
вторичной обмотки с
![]() заменяется расчётной электрически
эквивалентной цепью. При этом
электромагнитная мощность вторичной
обмотки реального трансформатора должна
быть равна электромагнитной мощности
вторичной обмотки приведённого
трансформатора, то есть
заменяется расчётной электрически
эквивалентной цепью. При этом
электромагнитная мощность вторичной
обмотки реального трансформатора должна
быть равна электромагнитной мощности
вторичной обмотки приведённого
трансформатора, то есть
![]() ,
где
,
где
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Из условия равенства потерь в активном
сопротивлении вторичной обмотки можно
получить следующее равенство:
![]() ,
следовательно,
,
следовательно,
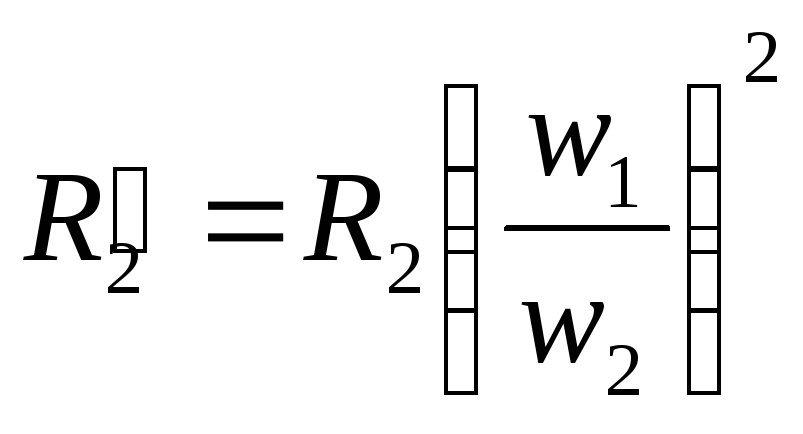 .
.
Из условия равенства реактивных мощностей
можно получить аналогичные выражения:
![]() ,
следовательно,
,
следовательно,
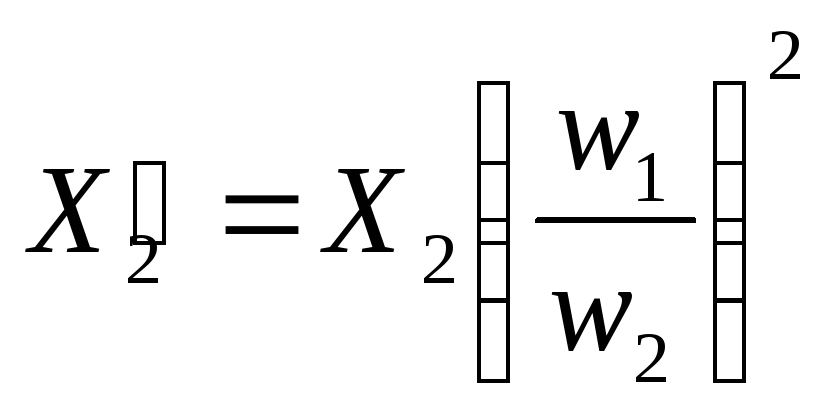 и
и
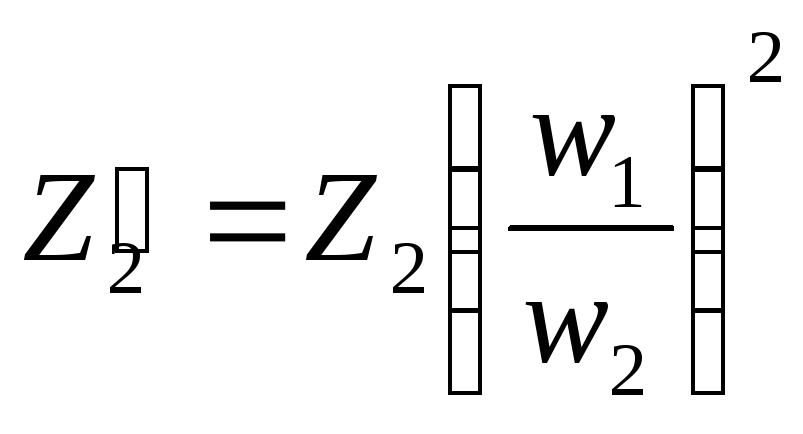 .
.
Таким образом, вместо реального
трансформатора мы получаем энергетически
эквивалентный трансформатор с
коэффициентом трансформации
![]() равным единице, который называется
приведённым.
равным единице, который называется
приведённым.
![]() ;
;
![]() ;
;
![]() .
.
Приведённым уравнения соответствует Т-образная электрическая схема замещения.
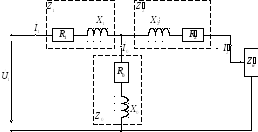
В этой схеме магнитная связь между
первичной и вторичной обмоткой заменена
электрической, а именно ветвью
намагничивания с параметрами
![]() и
и
![]() ,
которые определяются током холостого
хода
,
которые определяются током холостого
хода
![]() .
.
Все параметры, кроме
![]() ,
являются постоянными для данного
трансформатора, и могут быть определены
с помощью опытов холостого хода и
короткого замыкания.
,
являются постоянными для данного
трансформатора, и могут быть определены
с помощью опытов холостого хода и
короткого замыкания.
П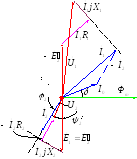 остроим
векторную диаграмму следующих уравнений:
остроим
векторную диаграмму следующих уравнений:
![]() ;
;
![]() ;
;
![]() .
Такая диаграмма называется диаграммой
привидения трансформатора для
активно-реактивной нагрузки.
.
Такая диаграмма называется диаграммой
привидения трансформатора для
активно-реактивной нагрузки.
Для построения вектора
![]() необходимо знать характер нагрузки (в
нашем случае нагрузка носит
активно-реактивный характер).
необходимо знать характер нагрузки (в
нашем случае нагрузка носит
активно-реактивный характер).
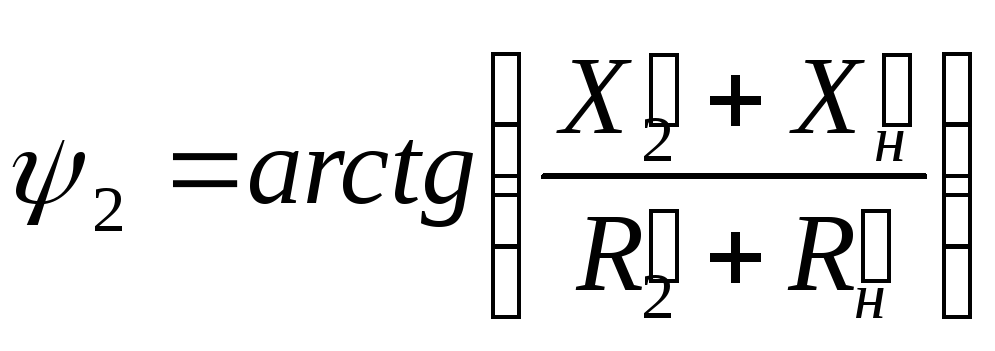 ;
;
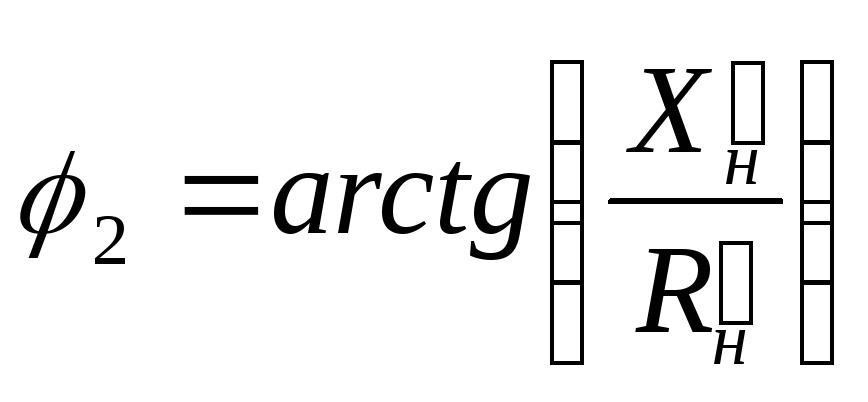 .
.
Все параметры в
схеме замещения, кроме
![]() ,
являются постоянными для данного
трансформатора, и могут быть определены
из опытов холостого хода и короткого
замыкания.
,
являются постоянными для данного
трансформатора, и могут быть определены
из опытов холостого хода и короткого
замыкания.
Опыт холостого хода.
![]() ;
;
![]() .
.
При холостом ходе
сопротивление нагрузки очень велико,
то есть
![]() ,
поэтому ток через вторичную цепь не
течёт, то есть
,
поэтому ток через вторичную цепь не
течёт, то есть
![]() .
.
По данным опыта
холостого хода можно определить
коэффициент трансформации
![]() .
Ток холостого хода в процентах от
номинального определяется по формуле:
.
Ток холостого хода в процентах от
номинального определяется по формуле:
![]() .
.
С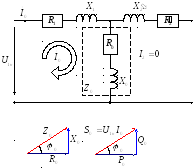 хема
замещения для опыта холостого хода.
хема
замещения для опыта холостого хода.
Так как сопротивление
![]() много меньше сопротивления
много меньше сопротивления
![]() ,
то модуль сопротивления можно найти по
формуле:
,
то модуль сопротивления можно найти по
формуле:
![]() ,
тогда
,
тогда
![]() ,
следовательно,
,
следовательно,
![]() .
.
![]() ;
;
![]() .
.
Опыт короткого замыкания:
П ри
опыте короткого замыкания сопротивление
нагрузки равно нулю, то есть
ри
опыте короткого замыкания сопротивление
нагрузки равно нулю, то есть
![]() ,
поэтому напряжение на зажимах вторичной
обмотки также равно нулю, то есть
,
поэтому напряжение на зажимах вторичной
обмотки также равно нулю, то есть
![]() .
При эксплуатации трансформатора, режим
при котором входное напряжение равно
номинальному считается аварийным. При
проведении опыта короткого замыкания
входное напряжение снижают до нуля и
только потом закорачивают проводником
вторичную обмотку, а затем постепенно
увеличивают входное напряжение до
значения, при котором токи в обмотках
станут равными номинальным. Такое
напряжение называется номинальным
напряжением короткого замыкания, и
выражается в процентах от номинального
напряжения:
.
При эксплуатации трансформатора, режим
при котором входное напряжение равно
номинальному считается аварийным. При
проведении опыта короткого замыкания
входное напряжение снижают до нуля и
только потом закорачивают проводником
вторичную обмотку, а затем постепенно
увеличивают входное напряжение до
значения, при котором токи в обмотках
станут равными номинальным. Такое
напряжение называется номинальным
напряжением короткого замыкания, и
выражается в процентах от номинального
напряжения:
![]() .
Для силовых трансформаторов это
пять-десять процентов, так как магнитны
поток
.
Для силовых трансформаторов это
пять-десять процентов, так как магнитны
поток
![]() в магнитопроводе пропорционален
напряжению на зажимах первичной обмотки
в магнитопроводе пропорционален
напряжению на зажимах первичной обмотки
![]() ,
а величина
,
а величина
![]() мала, следовательно, магнитный поток
мала, следовательно, магнитный поток
![]() тоже мал и для его создания требуется
малый намагничивающий ток, поэтому ток
тоже мал и для его создания требуется
малый намагничивающий ток, поэтому ток
![]() считают равным нулю.
считают равным нулю.
С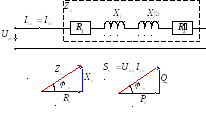 хема
замещения для опыта короткого замыкания.
хема
замещения для опыта короткого замыкания.
![]() ;
;
![]() .
.
Пользуясь этой
схемой определяют параметры обмоток.
По закону Ома:
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Приближённо можно
считать, что
![]() и
и
![]() .
.
