- •Электрические цепи постоянного тока.
- •Энергетический баланс.
- •Принцип (метод) наложения.
- •Преобразование схемы типа «звезда» в схему типа «треугольник».
- •Метод эквивалентного генератора.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Электрические цепи однофазного синусоидального тока.
- •Конденсатор в цепи синусоидального тока.
- •Основы символического метода:
- •Активная, реактивная и полная мощности.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Трёхфазные цепи.
- •Расчёт трёхфазных цепей.
- •Активная, реактивная и полная мощности трёхфазных цепей.
- •Измерение активной мощности трёхфазной цепи.
- •Магнитные цепи.
- •Уравнения напряжений и токов трансформатора.
- •Уравнения магнитодвижущих сил и токов.
- •Изменение вторничного напряжения.
- •Потери энергии в трансформаторе.
- •PГруппы соединений трёхфазных трансформаторов.
- •Вращающееся магнитное поле.
- •Получение кругового вращающегося магнитного поля.
- •Принцип действия асинхронного двигателя.
- •Устройство асинхронного двигателя.
- •Формула для нахождения частоты вращающегося поля.
- •Эдс статора и неподвижного ротора. Режим холостого хода.
- •Эдс вращающегося ротора.
- •Устойчивая работа двигателя.
- •Влияние изменения напряжения сети.
- •Регулировка скорости вращения асинхронного двигателя.
- •Тормозные режимы.
- •Синхронный двигатель.
- •Влияние тока возбуждения на работу двигателя.
- •Пуск синхронного двигателя.
- •Выпрямление переменного напряжения.
Передача энергии от активного двухполюсника к нагрузке.
Н айдёт
ток по методу эквивалентного генератора:
айдёт
ток по методу эквивалентного генератора:
![]() .
.
Выясним, при каких условиях в нагрузке
будет выделяться максимальная мощность.
Внутренние активные и реактивные
сопротивления
![]() и
и
![]() изменить нельзя, так как это параметры
самой цепи. Если реактивное сопротивление
нагрузки
изменить нельзя, так как это параметры
самой цепи. Если реактивное сопротивление
нагрузки
![]() подобрать равным реактивному внутреннему
сопротивлению
подобрать равным реактивному внутреннему
сопротивлению
![]() ,
то двухполюсник будет работать в
резонансном режиме и ток
,
то двухполюсник будет работать в
резонансном режиме и ток
![]() ,
текущий через нагрузку будет совпадать
по фазе с напряжением
,
текущий через нагрузку будет совпадать
по фазе с напряжением
![]() ,
то есть
,
то есть
![]() .
.
Так как же в цепи постоянного тока
максимальная мощность
![]() выделятся в случае, когда активное
сопротивление нагрузки
выделятся в случае, когда активное
сопротивление нагрузки
![]() равно активному внутреннему сопротивлению
двухполюсника
равно активному внутреннему сопротивлению
двухполюсника
![]() .
.
Таким образом, существует два условия
выделения максимальной мощности на
нагрузке:
![]() и
и
![]() .
.
Трёхфазные цепи.
Трёхфазная симметричная система ЭДС
– совокупность трёх синусоидальных
ЭДС одинаковой частоты и амплитуды, но
сдвинутых на 120 градусов друг от друга,
то есть
![]() ;
;
![]() ;
;
![]() ,
или
,
или
![]() ;
;
![]() ;
;
![]() ,
где
,
где
![]()

Трёхфазная цепь – совокупность трёхфазной системы ЭДС, трёхфазной нагрузки и соединительных проводов.
В подавляющем большинстве случаев для передачи энергии используются трёхфазные цепи.
Так как векторная сумма ЭДС равна нулю,
то в случае, если нагрузка не присоединена
к зажимам
![]() ,
,
![]() ,
,
![]() ,
то по обмоткам генератора ток протекать
не будет.
,
то по обмоткам генератора ток протекать
не будет.
Трёхфазного источника в цепях обозначается следующим образом:

Существует пять простейших способов соединения трёхфазного генератора с трёхфазной нагрузкой:
-
«Звезда-звезда» с нулевым проводом.
-
«Звезда-звезда» без нулевого провода.
-
«Звезда-треугольник»
-
«Треугольник-треугольник».
-
«
 Треугольник-звезда»
Треугольник-звезда»
Нулевой провод – провод, соединяющий нулевые точки генератора и нагрузки.
Линейные провода – провода,
соединяющие точки
![]() ,
,
![]() и
и
![]() генератора и нагрузки.
генератора и нагрузки.
Линейные токи – токи, текущие через линейные провода.
Линейные напряжения – напряжения между линейными проводами.
Фаза генератора – каждая и трёх обмоток генератора.
Фаза нагрузки – каждая из трёх нагрузок.
Фазовые токи – токи, протекающие через фазы генератора и нагрузки.
Фазовые напряжения – напряжения на фазах генератора и нагрузки.
При присоединении трёхфазного генератора
«звездой» линейное напряжение по модулю
в
![]() больше фазного.
больше фазного.
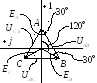
![]() ;
;
![]() ;
;
![]()
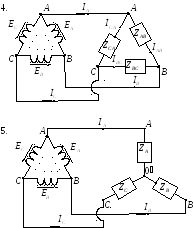 ;
;
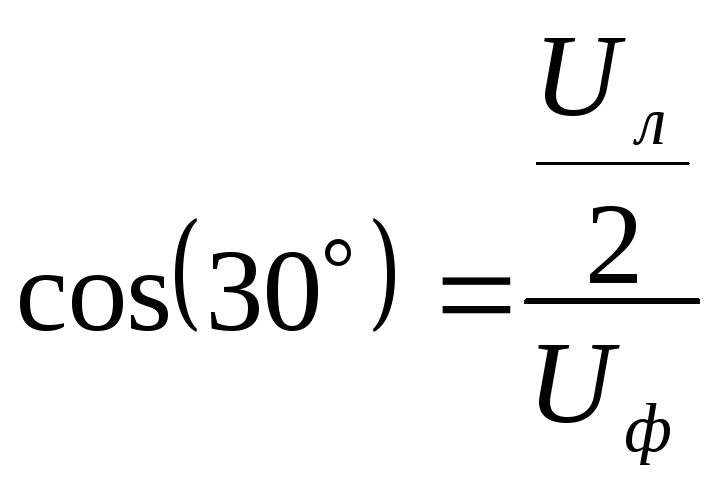 ;
;
![]()
![]() ;
;
Линейные напряжения:
![]() ;
;
![]() ;
;
![]() .
.
При присоединении генератора
«треугольником» линейное напряжение
равно фазовому, то есть
![]() .
.
При присоединении нагрузки «треугольником» положительное направление токов выбирают по часовой стрелке, при этом линейные токи не равны фазовым. Но линейные токи можно найти с помощью фазовых, используя первый закон Кирхгофа.
Расчёт трёхфазных цепей.
Так как трёхфазовые цепи являются разновидностью цепей синусоидального тока, то расчёт и исследование их проводят с помощью тех же методов. Возможно применение так же символического метода. Кроме того, аналитический расчёт следует сопровождать построением векторных диаграмм.
Рассмотрим схему типа «звезда-звезда» с нулевым проводом.
Е сли
нулевой провод обладает малым
сопротивлением, то потенциал точки
сли
нулевой провод обладает малым
сопротивлением, то потенциал точки
![]() можно считать равным потенциалу точки
можно считать равным потенциалу точки
![]() ,
то есть нулевой провод можно закоротить
и схема преобразуется в три независимых
контура.
,
то есть нулевой провод можно закоротить
и схема преобразуется в три независимых
контура.
Токи в этих контурах можно найти по
следующим формулам:
![]() ;
;
![]() ;
;
![]() .
Ток, текущий через нулевой провод можно
найти по первому закону Кирхгофа:
.
Ток, текущий через нулевой провод можно
найти по первому закону Кирхгофа:
![]() .
В случае равномерной (симметричной)
нагрузки, при которой выполняется
условие
.
В случае равномерной (симметричной)
нагрузки, при которой выполняется
условие
![]() ,
нулевой ток равен нулю.
,
нулевой ток равен нулю.
Допустим, что сопротивление нагрузок
равны, то есть
![]() .
В этом случае токи, текущие через линейный
провода можно найти по следующим
формулам:
.
В этом случае токи, текущие через линейный
провода можно найти по следующим
формулам:
![]() ,
,
![]() ,
,
![]() .
.
Нулевой провод может быть изъят из цепи без изменения её работы.
Построим векторную диаграмму.
П ри
неравномерной нагрузке фаз нулевой ток
уже не будет равен нулю.
ри
неравномерной нагрузке фаз нулевой ток
уже не будет равен нулю.
При наличии в нулевом проводе сопротивления расчёт производится методом двух узлов.
Рассмотрим случай неравномерной нагрузки.
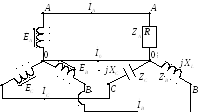
Дано:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Аналитический способ решения:
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
Г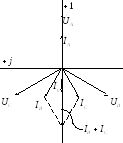 еометрический
метод решения с помощью векторных
диаграмм:
еометрический
метод решения с помощью векторных
диаграмм:
![]() ;
;
![]() .
.
Рассмотрим соединение типа «звезда-треугольник».
Т ок
ок
![]() вызван напряжением между точками
вызван напряжением между точками
![]() и
и
![]() ,
поэтому его можно найти по следующей
формуле:
,
поэтому его можно найти по следующей
формуле:
![]() .
.
Аналогично можно найти токи
![]() и
и
![]() ,
которые вызваны напряжениями между
точками
,
которые вызваны напряжениями между
точками
![]() и
и
![]() и точками
и точками
![]() и
и
![]() ,
соответственно, поэтому их можно найти
по следующим формулам:
,
соответственно, поэтому их можно найти
по следующим формулам:
![]() и
и
![]() .
.
Линейные токи определяются через фазовые
токи по первому закону Кирхгофа, то
есть:
![]() ;
;
![]() ;
;
![]() .
.
Рассмотрим случай равномерной нагрузки,
то есть
![]() .
.
В этом случае токи можно найти по
следующим формулам:
![]() ,
,
![]() ,
,
![]() .
Так нагрузка равномерная, то модули
этих токов будут равны, то есть:
.
Так нагрузка равномерная, то модули
этих токов будут равны, то есть:![]() .
.
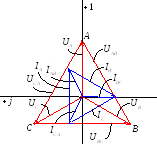 При
равномерной нагрузке фаз линейные токи
по модулю в
При
равномерной нагрузке фаз линейные токи
по модулю в
![]() раз больше фазовых токов нагрузки, то
есть:
раз больше фазовых токов нагрузки, то
есть:
![]() ;
;
![]() ;
;
![]() .
.
Если нагрузка равномерная, то линейное
напряжение равно фазовому (![]() ),
а линейный ток больше в
),
а линейный ток больше в
![]() раз фазового (
раз фазового (![]() ).
).
Рассмотрим случай неравномерной нагрузки.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Линейные напряжения:
![]() ;
;
![]() ;
;
![]() .
.
Ф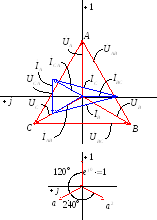 азовые
токи:
азовые
токи:
![]() ;
;
![]() ;
;
![]() .
.
Линейные токи:
![]() ;
;
![]() ;
;
![]() .
.
Комплексное число
![]() по модулю равно единице. Обозначим это
комплексное число за
по модулю равно единице. Обозначим это
комплексное число за
![]() - оператор трёхфазной цепи. Тогда:
- оператор трёхфазной цепи. Тогда:
![]() ,
а
,
а
![]() ,
,
![]()
![]() .
.
Схема типа «звезда-звезда» без нулевого провода.
Т акая
схема решается с помощью метода двух
узлов.
акая
схема решается с помощью метода двух
узлов.
![]() .
.
Токи в ветвях определяются с помощью законов Ома:
![]() ;
;
![]() ;
;
![]() .
.
Если нагрузка равномерная, то есть
![]() ,
то:
,
то:
![]()
![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
![]() .
.
Пример:
Рассмотрим схему типа «звезда-звезда»,
у которой
![]() ,
,
![]() ,
,
![]() ,
тогда:
,
тогда:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.