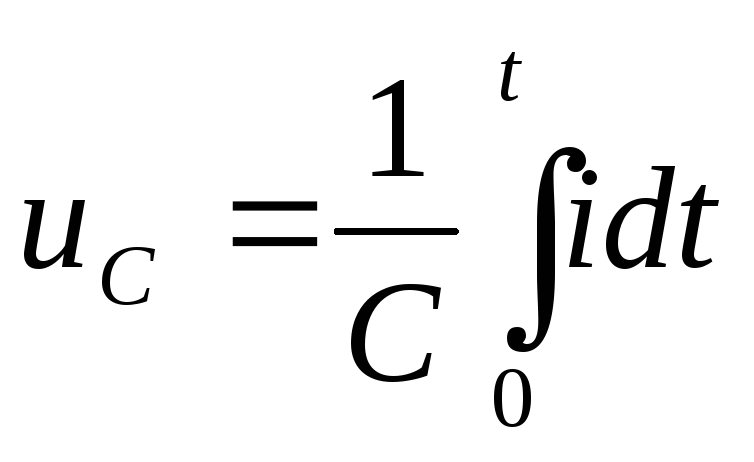- •Электрические цепи постоянного тока.
- •Энергетический баланс.
- •Принцип (метод) наложения.
- •Преобразование схемы типа «звезда» в схему типа «треугольник».
- •Метод эквивалентного генератора.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Электрические цепи однофазного синусоидального тока.
- •Конденсатор в цепи синусоидального тока.
- •Основы символического метода:
- •Активная, реактивная и полная мощности.
- •Передача энергии от активного двухполюсника к нагрузке.
- •Трёхфазные цепи.
- •Расчёт трёхфазных цепей.
- •Активная, реактивная и полная мощности трёхфазных цепей.
- •Измерение активной мощности трёхфазной цепи.
- •Магнитные цепи.
- •Уравнения напряжений и токов трансформатора.
- •Уравнения магнитодвижущих сил и токов.
- •Изменение вторничного напряжения.
- •Потери энергии в трансформаторе.
- •PГруппы соединений трёхфазных трансформаторов.
- •Вращающееся магнитное поле.
- •Получение кругового вращающегося магнитного поля.
- •Принцип действия асинхронного двигателя.
- •Устройство асинхронного двигателя.
- •Формула для нахождения частоты вращающегося поля.
- •Эдс статора и неподвижного ротора. Режим холостого хода.
- •Эдс вращающегося ротора.
- •Устойчивая работа двигателя.
- •Влияние изменения напряжения сети.
- •Регулировка скорости вращения асинхронного двигателя.
- •Тормозные режимы.
- •Синхронный двигатель.
- •Влияние тока возбуждения на работу двигателя.
- •Пуск синхронного двигателя.
- •Выпрямление переменного напряжения.
Конденсатор в цепи синусоидального тока.
Если напряжение, приложенное к
конденсатору, не меняется во времени,
то заряд
![]() на обкладке и заряд
на обкладке и заряд
![]() на другой неизменны и ток
на другой неизменны и ток
![]() через конденсатор не течёт, то есть
через конденсатор не течёт, то есть
![]() .
.
Если же напряжение на конденсаторе
меняется во времени, например по
синусоидальному закону
![]() ,
то заряд будет меняться по синусоидальному
закону
,
то заряд будет меняться по синусоидальному
закону
![]() и конденсатор будет периодически
перезаряжаться. Это сопровождается
протеканием следующего тока:
и конденсатор будет периодически
перезаряжаться. Это сопровождается
протеканием следующего тока:
![]()
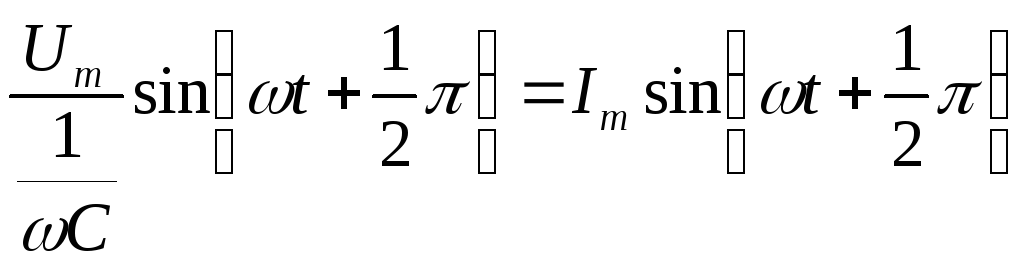 .
Комплексные значения тока и напряжения
будут иметь следующий вид:
.
Комплексные значения тока и напряжения
будут иметь следующий вид:
![]() ;
;
![]() .
.
Построим векторную диаграмму:
М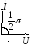 ожно
сделать вывод, что ток, протекающий
через конденсатор, опережает напряжение
на конденсаторе по фазе на
ожно
сделать вывод, что ток, протекающий
через конденсатор, опережает напряжение
на конденсаторе по фазе на
![]() .
.
Ёмкостное сопротивление
![]() .
.
Если
![]() ,
то
,
то
![]() ,
то есть конденсатор можно заменить
разрывом цепи.
,
то есть конденсатор можно заменить
разрывом цепи.
Если
![]() ,
то
,
то
![]() ,
то есть конденсатор можно заменить
проводником.
,
то есть конденсатор можно заменить
проводником.
Зависимость
![]() от
от
![]() выглядит следующим образом:
выглядит следующим образом:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Мгновенная мощность цепи
![]() .
.
Видно, что происходит обмен энергией между источником и электрическим полем конденсатора.
С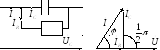 хема
замещения реального конденсатора:
хема
замещения реального конденсатора:
Построим векторную диаграмму:
По первому закону Кирхгофа построим
векторную диаграмму тока:
![]() .
.
Так как фаза тока больше фазы сопротивления,
то
![]() ,
что характерно для цепи ёмкостного
характера.
,
что характерно для цепи ёмкостного
характера.
Основы символического метода:
Этот метод позволяет перейти от уравнений, составленных для мгновенных значений и являющихся интегро-дифференциальными, к алгебраическим уравнениям, составленным для комплексов токов и напряжений. Переход основан на замене реального мгновенного значения его символом.
|
Мгновенные значения |
Символы |
Примечания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример:
П о
второму закону Кирхгофа:
о
второму закону Кирхгофа:
![]() ;
;
![]() .
.
Заменим мгновенные значения их символами:
![]() .
.
Получим алгебраическое уравнение относительно тока:
![]() ,
где
,
где
![]() - комплексное сопротивление цепи.
- комплексное сопротивление цепи.
Отсюда
![]() .
Перейдя к мгновенным значениям можно
найти
.
Перейдя к мгновенным значениям можно
найти
![]() .
.
Рассмотрим комплексное сопротивление
цепи:
![]() ,
где
,
где
![]() - реактивное сопротивление цепи. Тогда
- реактивное сопротивление цепи. Тогда
![]() .
.
Комплексная проводимость:
![]() .
.
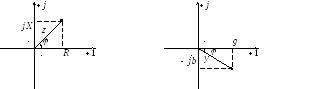
Таким образом, закон Ома можно записать
двумя способами:
![]() .
.
Законы Кирхгофа также справедливы в символической форме.
Первый закон Кирхгофа в символической
форме:![]() .
.
Второй закон Кирхгофа в символической
форме:
![]() .
.
Следовательно, в символической форме справедливы все методы расчёта электрической цепи, вывод которых основан на законах Кирхгофа, то есть все известные методы.
Активная, реактивная и полная мощности.
Активная мощность
![]() - среднее значение мгновенной мощности
- среднее значение мгновенной мощности
![]() за период
за период
![]() ;
;
![]() ,
,
![]() .
Мощность
.
Мощность
![]() это энергия, которая выделяется в виде
тепла в единицу времени на участке цепи
сопротивлением
это энергия, которая выделяется в виде
тепла в единицу времени на участке цепи
сопротивлением
![]() .
.
Реактивная мощность
![]() - энергия, которой обмениваются источник
энергии и приёмник;
- энергия, которой обмениваются источник
энергии и приёмник;
![]() ,
,
![]() .
.
Полная мощность
![]() - мощность, которую источник может
отдавать потребителю, если потребитель
будет работать при
- мощность, которую источник может
отдавать потребителю, если потребитель
будет работать при
![]() ,
то есть потребитель будет являться
активным сопротивлением;
,
то есть потребитель будет являться
активным сопротивлением;
![]() ,
,
![]() .
.
Связь между активной, реактивной и
полной мощностью:
![]() .
.
На щитке источника электроэнергии
переменного тока указывают именно
величину полной мощности
![]() .
.
Комплексная мощность
![]() ,
где
,
где
![]() ,
,
![]() .
Подставив, получим:
.
Подставив, получим:
![]()
![]() .
Откуда можно получить следующую формулу:
.
Откуда можно получить следующую формулу:
![]() .
.
Измерение активной мощности ваттметром.
В аттметр
имеет четыре вывода: два для измерения
тока и два для измерения напряжения.
Выводами для измерения тока он включается
в ветвь цепи последовательно, как
амперметр. Он измеряет втекающий в точку
(*) ток. Другие два вывода, предназначенные
для измерения напряжения, включаются
параллельно ветви цепи. Если точка (*)
стоит около точки
аттметр
имеет четыре вывода: два для измерения
тока и два для измерения напряжения.
Выводами для измерения тока он включается
в ветвь цепи последовательно, как
амперметр. Он измеряет втекающий в точку
(*) ток. Другие два вывода, предназначенные
для измерения напряжения, включаются
параллельно ветви цепи. Если точка (*)
стоит около точки
![]() ,
то ваттметр измеряет напряжение
,
то ваттметр измеряет напряжение
![]() ,
тогда активную мощность можно найти по
следующей формуле:
,
тогда активную мощность можно найти по
следующей формуле:
![]() .
.
Применение векторных диаграмм.
Д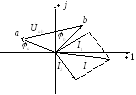 опустим:
опустим:
![]() ;
;
![]() ;
;
Тогда:
![]() ;
;
![]() ;
;
Для того, что бы построить вектор суммы нескольких векторов нужно из конца первого вектора построить второй, из конца второго третий и так далее, а затем соединить начало первого вектора с концом последнего.
Для того, что бы построить вектор разности двух векторов нужно соединить конец вычитаемого вектора с концом уменьшаемого вектора.
Диаграмма токов всегда строится по первому закону Кирхгофа, а диаграмма напряжений всегда строится по второму закону Кирхгофа.
Пример:
Д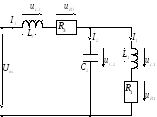 ано:
ано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Требуется построить векторную диаграмму.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
 ;
;
![]() ;
;
![]() ;
;
Рассмотрим схему:
Д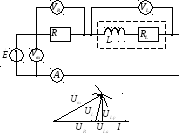 иаграмму
для напряжений строится по второму
закону Кирхгофа:
иаграмму
для напряжений строится по второму
закону Кирхгофа:
![]() .
Так как неизвестны сдвиги по фазам
напряжений
.
Так как неизвестны сдвиги по фазам
напряжений
![]() и
и
![]() ,
то они строятся с помощью метода засечек.
Строятся окружности радиусом
,
то они строятся с помощью метода засечек.
Строятся окружности радиусом
![]() и
и
![]() из конца и начала вектора
из конца и начала вектора
![]() соответственно. Эти окружности
пересекаются в двух точках. Исходя из
физического смысла, выбираем верхнюю
точку. Соединив точку пересечения с
началом и концом вектора
соответственно. Эти окружности
пересекаются в двух точках. Исходя из
физического смысла, выбираем верхнюю
точку. Соединив точку пересечения с
началом и концом вектора
![]() ,
можно получить расположение векторов
,
можно получить расположение векторов
![]() и
и
![]() .
Проекция вектора
.
Проекция вектора
![]() на ось действительных чисел даст нам
вектор активного сопротивления катушки
на ось действительных чисел даст нам
вектор активного сопротивления катушки
![]() ,
а на ось комплексных чисел – вектор
реактивного сопротивления катушки.
,
а на ось комплексных чисел – вектор
реактивного сопротивления катушки.
Топографическая диаграмма.
П отенциал
какой-нибудь одной точки, например точки
отенциал
какой-нибудь одной точки, например точки
![]() ,
принимается за ноль, то есть
,
принимается за ноль, то есть
![]() .
Затем определяются потенциалы точек
цепи и положение их на комплексной
плоскости.
.
Затем определяются потенциалы точек
цепи и положение их на комплексной
плоскости.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Резонансный режим
работы двухполюсника.
Явление резонанса возможно в цепи, которая содержит реактивные элементы разного знака, то есть в цепи, которая содержит индуктивность и ёмкость.
Резонанс – режим, при котором то к
и напряжение на входе двухполюсника
совпадают по фазе, то есть разность фаз
![]() равна нулю. Это основное условие любого
резонанса. По отношению к внешней цепи
двухполюсник ведёт себя, как активное
сопротивление.
равна нулю. Это основное условие любого
резонанса. По отношению к внешней цепи
двухполюсник ведёт себя, как активное
сопротивление.
Различают два вида резонансов: резонанс токов и резонанс напряжений.
Резонанс токов.
П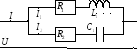 ри
параллельном соединении катушки
индуктивности и конденсатора возникает
резонанс токов при определённых условиях.
ри
параллельном соединении катушки
индуктивности и конденсатора возникает
резонанс токов при определённых условиях.
Определим токи:
![]() ;
;
![]() ;
;
![]() .
.
Из полученного уравнения и из основного
условия резонанса
![]() можно получить условие резонансов
токов:
можно получить условие резонансов
токов:
![]() .
Так как
.
Так как
![]() ,
а
,
а
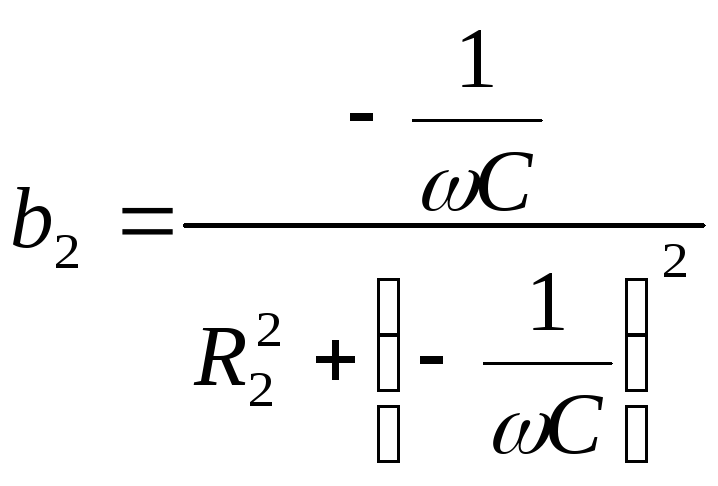 ,
то условие резонансов токов приобретает
следующий вид:
,
то условие резонансов токов приобретает
следующий вид:
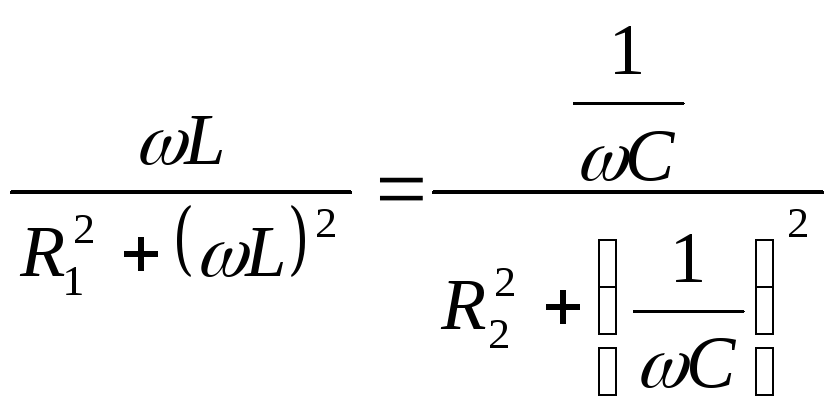 .
.
Построим векторную диаграмму.
Если активные внутренние сопротивления
катушки индуктивности и конденсатора
не равны нулю, то
![]() ,
,
![]() .
.
Если активное внутреннее сопротивление
конденсатора очень мало, то условие
резонанса токов примет следующий вид:
![]() .
.
Если активные внутренние сопротивления
катушки и индуктивности и конденсатора
равны нулю, то условие резонанса примет
следующий вид:
![]() ,
откуда
,
откуда
![]() .
При этом
.
При этом
![]() .
.
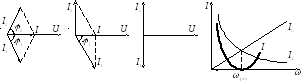
Ток, текущий через катушку индуктивности
можно найти по формуле:
![]() .
Если
.
Если
![]() ,
то ток через катушку индуктивности
будет равен нулю, то есть
,
то ток через катушку индуктивности
будет равен нулю, то есть
![]() .
.
Реактивные проводимости:
![]() ;
;
![]() ;
;
![]() .
.
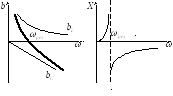
Задачи:
Требуется построить зависимость токов
через катушку и конденсатор, в зависимости
от ёмкости конденсатора
![]() .
.
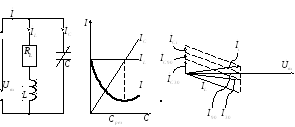
Ток, текущий через катушку индуктивности,
можно найти по следующей формуле:
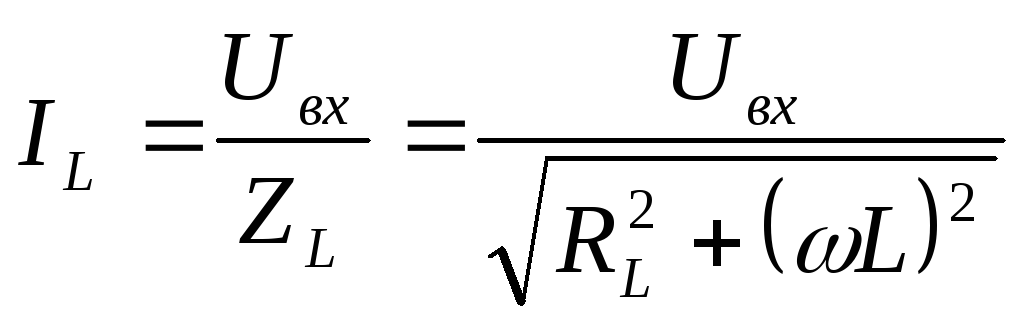 .
Из этой формулы видно, что ток, текущий
через катушку индуктивности, не зависит
от ёмкости конденсатора.
.
Из этой формулы видно, что ток, текущий
через катушку индуктивности, не зависит
от ёмкости конденсатора.
Если ёмкость конденсатора
![]() равна нулю, тогда
равна нулю, тогда
![]() ,
следовательно, ток, текущий через
конденсатор,
,
следовательно, ток, текущий через
конденсатор,
![]() равен нулю, а ток
равен нулю, а ток
![]() ,
который равен сумме токов, текущих через
катушку индуктивности и конденсатор,
будет равен току, текущему через катушку
индуктивности
,
который равен сумме токов, текущих через
катушку индуктивности и конденсатор,
будет равен току, текущему через катушку
индуктивности
![]() .
.
При увеличении ёмкости конденсатора
![]() будет увеличиваться ток, текущий через
него
будет увеличиваться ток, текущий через
него
![]() .
.
Компенсация сдвига фаз.
Входное сопротивление большинства
потребителей электроэнергии имеют
индуктивный характер. Для того, чтобы
уменьшить потребляемый ток и тем самым
снизить потери энергии, параллельно
приёмнику подключают батарею конденсатора,
то есть добиваются режима резонанса
тока. Этот процесс называют компенсацией
сдвига фаз. Обычно величину
![]() доводят до значений 0.9-0.95. Компенсация
сдвига фаз особенно важна для энергоёмких
потребителей.
доводят до значений 0.9-0.95. Компенсация
сдвига фаз особенно важна для энергоёмких
потребителей.
Резонанс напряжений.
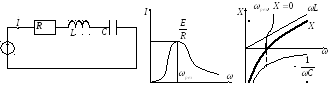
В цепи, в которой включены последовательно
конденсатор, катушка индуктивности и
конденсатор, возможно возникновение
резонанса напряжений при определённых
условиях. Ток, текущий в цепи можно найти
по формуле:
![]() ,
где
,
где
![]() .
Если нужно чтобы сдвиг по фазе между
напряжениями равнялся нулю, то надо
чтобы
.
Если нужно чтобы сдвиг по фазе между
напряжениями равнялся нулю, то надо
чтобы
![]() .
Следовательно,
.
Следовательно,
![]() - условие резонанса напряжений, при этом
резонансную частоту можно найти по
формуле:
- условие резонанса напряжений, при этом
резонансную частоту можно найти по
формуле:
![]() .
При резонансе
.
При резонансе
![]() ,
а ток
,
а ток
![]() .
.
Построим векторную диаграмму по второму закону Кирхгофа:
О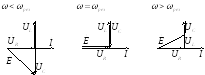 тношение
тношение
![]()
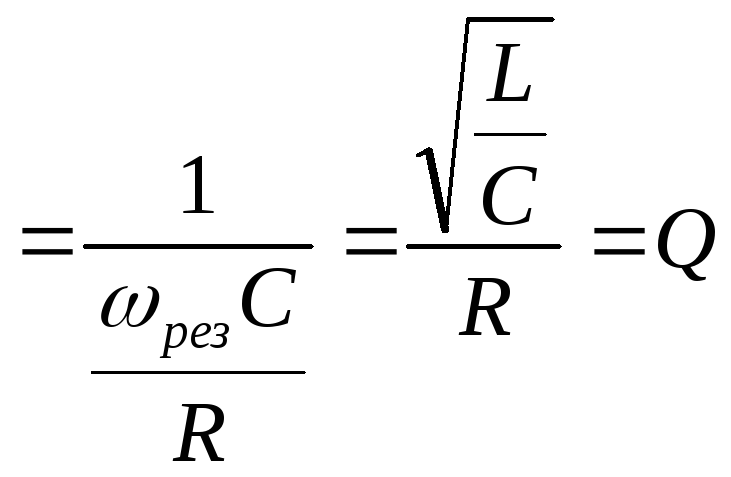 называют добротностью.
называют добротностью.
Добротность – величина, показывающая
во сколько раз напряжение на реактивном
элементе при резонансе больше чем
напряжение на входе, то есть
![]() .
.
Построим графики напряжений в зависимости от частоты.
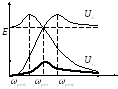 Напряжение
на катушке индуктивности можно найти
по формуле:
Напряжение
на катушке индуктивности можно найти
по формуле:
![]() .
При
.
При
![]() напряжение на катушке индуктивности
будет равняться нулю, при
напряжение на катушке индуктивности
будет равняться нулю, при
![]() напряжение на катушке индуктивности
будет равняться ЭДС источника, то есть
напряжение на катушке индуктивности
будет равняться ЭДС источника, то есть
![]()
Напряжение на конденсаторе можно найти
по формуле:
![]() .
Если
.
Если
![]() ,
то напряжение на конденсаторе равно
ЭДС источника, то есть
,
то напряжение на конденсаторе равно
ЭДС источника, то есть
![]() .
.
Видно, что графики имеют ярко выраженные максимумы.