
TERMODINAMIKA_EKZAMEN_2012
.docЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ
-
Фазовое пространство. Функция распределения. Статистическая независимость. Теорема Лиувилля.
-
Роль энергии. Энтропия. Закон возрастания энтропии.
-
Определение основных термодинамических величин (температура и давление).
-
Условия теплового и механического равновесия.
-
Работа и количество тепла. Теплоемкость. Основные термодинамические потенциалы.
-
Соотношения между термодинамическими производными.
-
Процесс Джоуля – Томсона.
-
Максимальная работа.
-
Термодинамические флуктуации основных физических величин.
-
Термодинамические неравенства.
-
Зависимость термодинамических величин от числа частиц.
-
Условия равновесия в системах с переменным числом частиц.
-
Условия равновесия во внешнем поле.
-
Уравнение Клайперона-Клаузиуса
-
Равновесие фаз с искривленной поверхностью
-
Условия равновесия однокомпонентных флюидов в рамках уравнения ван-дер-Ваальса
-
Преобразования Лежандра. Различные термодинамические потенциалы.
-
Распределение Гиббса. Свободная энергия и распределение Гиббса.
-
Идеальный газ. Распределение Больцмана. Свободная энергия идеального газа.
-
Уравнение состояния идеального газа. Идеальный газ с постоянной теплоемкостью.
-
Закон равнораспределения.
-
Отклонение газов от идеальности. Первый вириальный коэффициент.
-
Уравнение ван – дер – Ваальса. Свободная энергия газа ван – дер – Ваальса.
-
Уравнение Пенга-Робинсона. Свободная энергия в рамках уравнения Пенга-Робинсона
-
Приведенные уравнения состояния.
-
Критическая точка газа ван – дер – Ваальса.
-
Критическая точка в рамках уравнения Пенга-Робинсона.
-
Растворы. Правило фаз Гиббса
-
Термодинамический потенциал разбавленных растворов.
-
Условие равновесия по отношению к растворителю.
-
Условие равновесия по отношению к растворенному веществу
Задачи по термодинамике и статистической физике
-
Уравнение состояния газа имеет вид
![]() (
(![]() - число молей)
- число молей)
Найти выражение для плотности энтропии газа.
-
Два одинаковых идеальных газа с одинаковыми температурами
 и числами частиц
и числами частиц
 ,
но с разными давлениями
,
но с разными давлениями
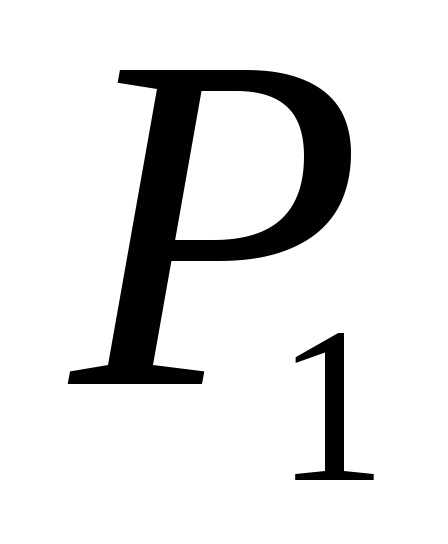 и
и
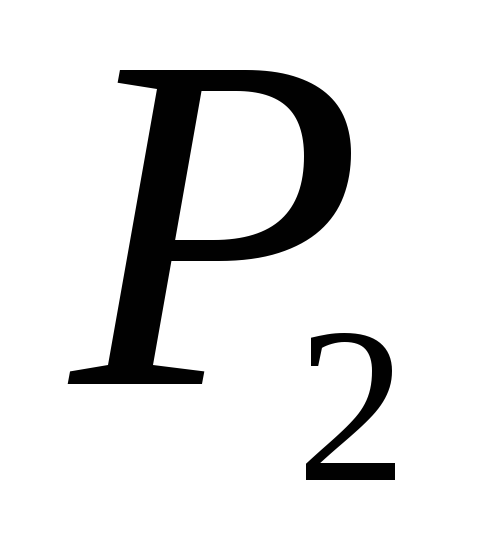 находятся в двух сосудах. Затем сосуды
соединяются; определить изменение
энтропии.
находятся в двух сосудах. Затем сосуды
соединяются; определить изменение
энтропии.
-
Два одинаковых идеальных газа с одинаковыми давлениями
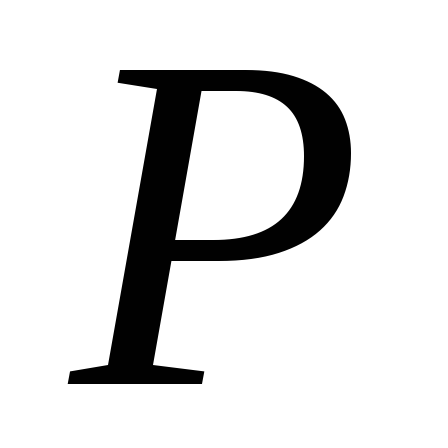 и числом частиц
и числом частиц
 .
Но с разными температурами
.
Но с разными температурами
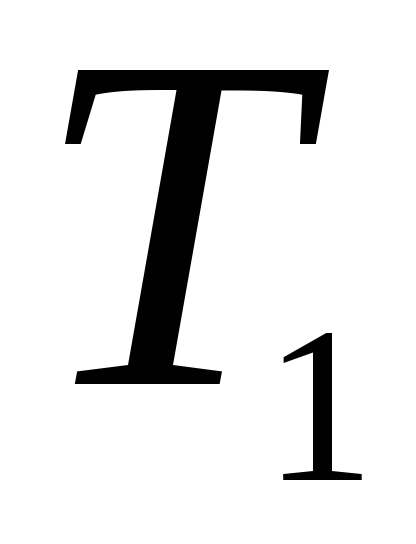 и
и
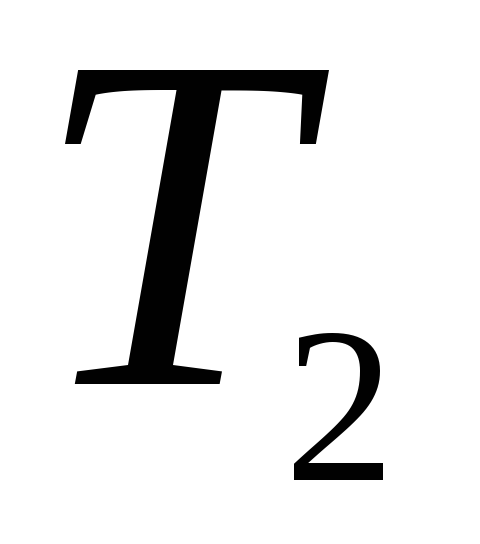 находятся в сосудах с объемами
находятся в сосудах с объемами
 и
и
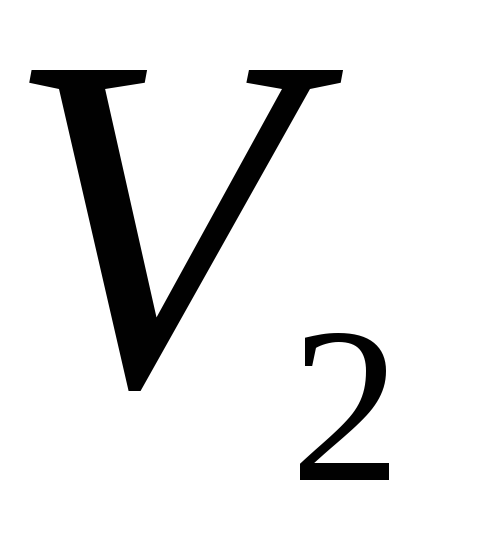 .
Затем сосуды соединяются. Найти изменение
энтропии.
.
Затем сосуды соединяются. Найти изменение
энтропии.
-
Найти работу, производимую над идеальным газом при адиабатическом сжатии.
-
Найти количества тепла, получаемого газом при процессе, происходящем при постоянном объеме (изохорном).
-
Найти работу и количества тепла при процессе, происходящем при постоянном давлении (изобарном).
-
Найти работу, совершаемую над газом и количества тепла, получаемое им при сжатии от объема
 до
до
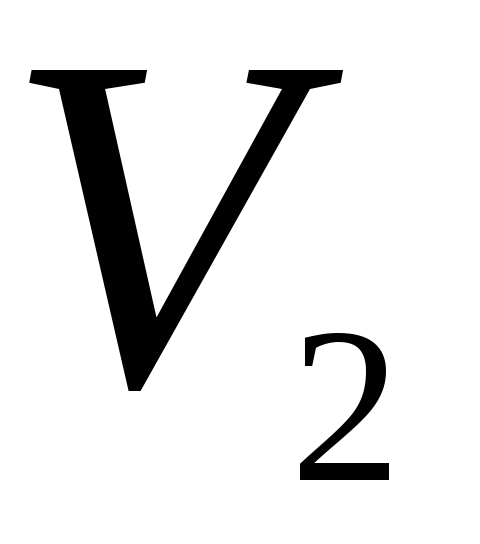 ,
согласно уравнению
,
согласно уравнению

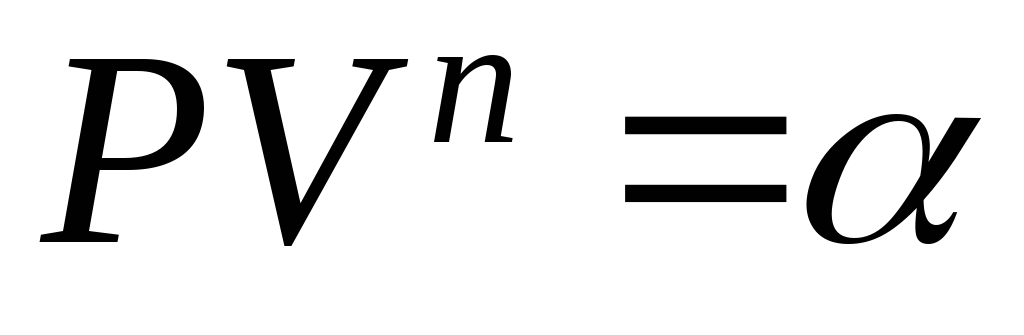 (политропический процесс).
(политропический процесс).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им, для цикла, состоящего из двух изохорных и двух изобарных процессов (последовательные состояния газа имеют давление и объем: 1)
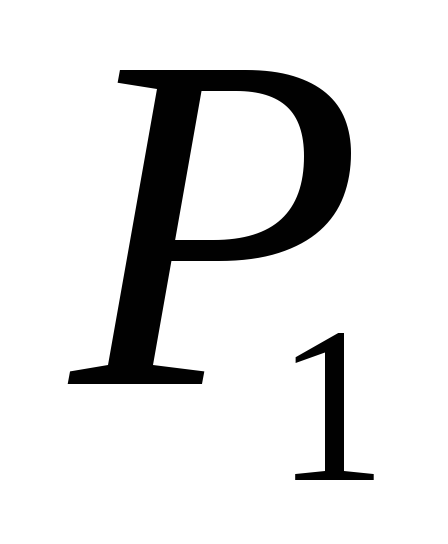 ,
,
 ; 2)
; 2)
 ,
,
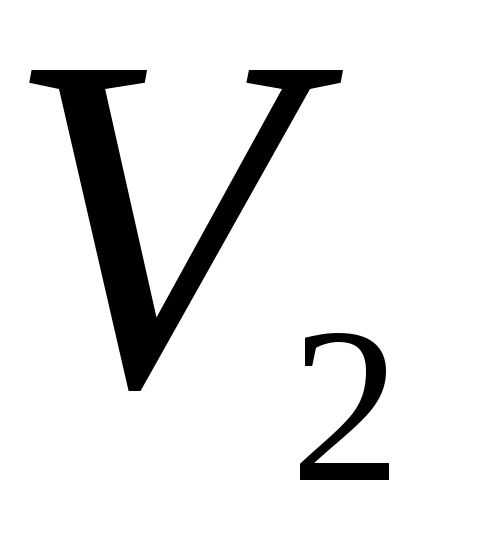 ;
3)
;
3)
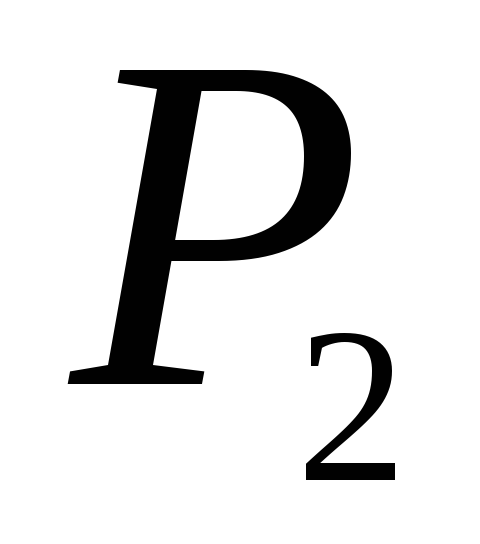 ,
,
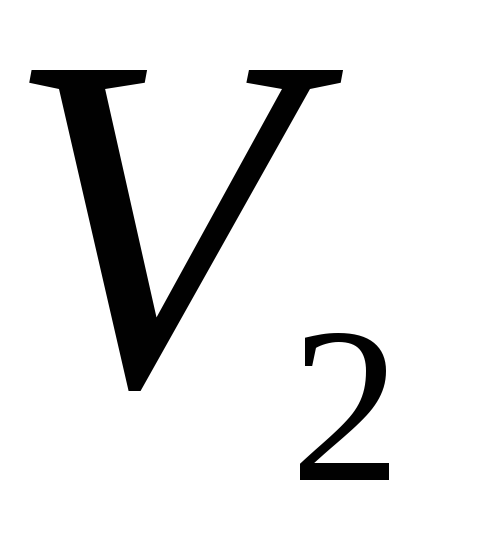 ;
4)
;
4)
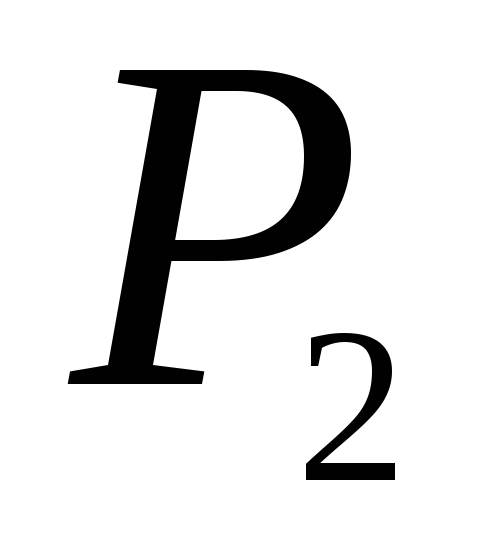 ,
,
 ;
5)
;
5)
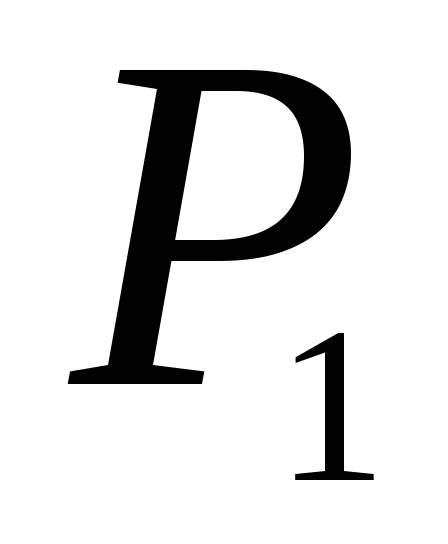 ,
,
 ).
).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им для цикла, состоящего из двух изохорных и двух изотермических процессов (последовательные состояния газа имеют объем и температуру: 1)
 ,
,
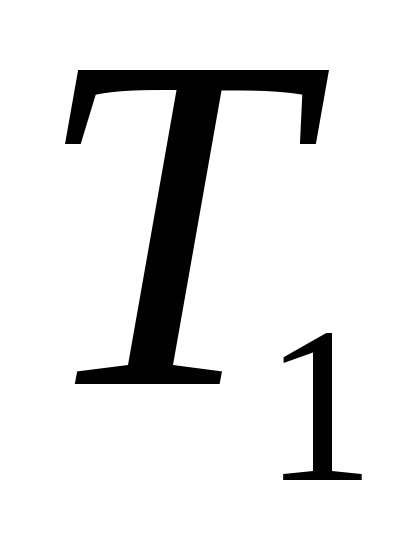 ;
2)
;
2)
 ,
,
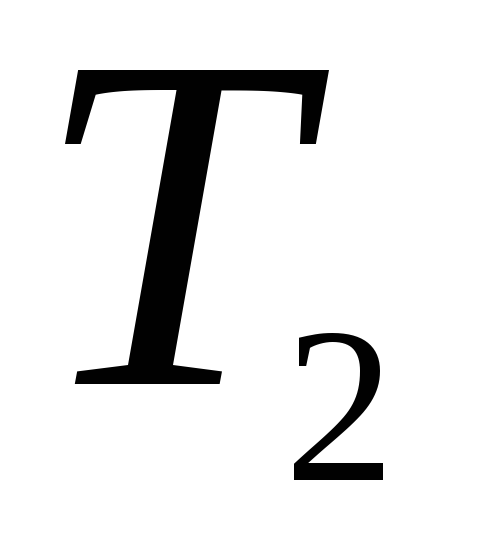 ;
3)
;
3)
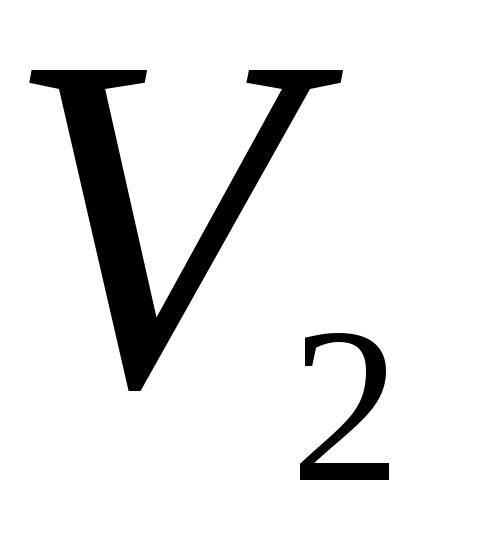 ,
,
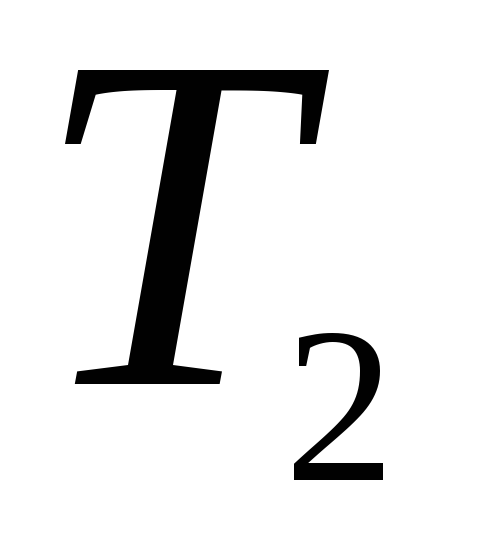 ;
4)
;
4)
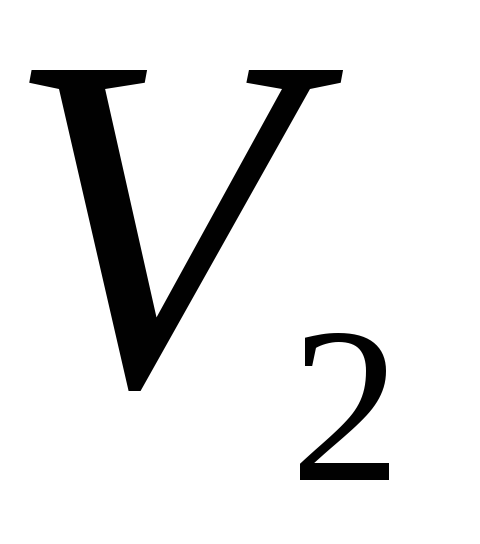 ,
,
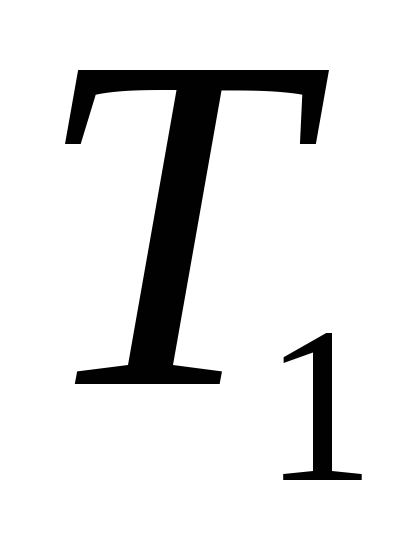 ;
5)
;
5)
 ,
,
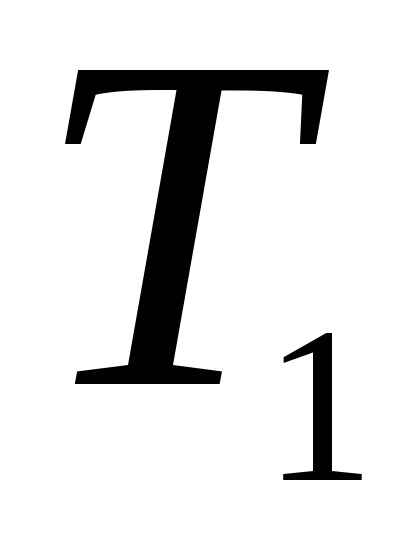 ).
).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им, для цикла из двух изотермических и двух адиабатических процессов (последовательные состояния имеют энтропию, температуру и давление: 1)
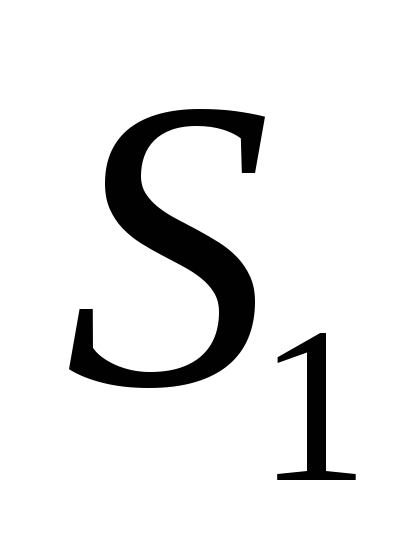 ,
,
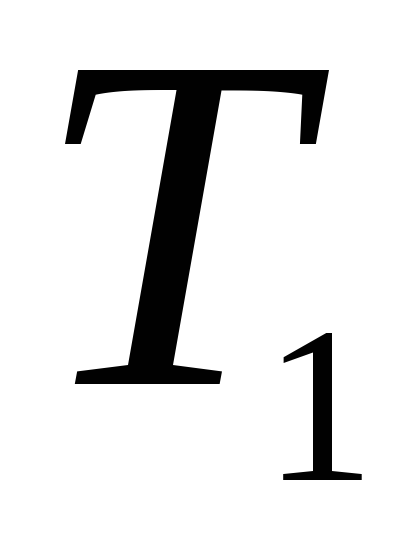 ,
,
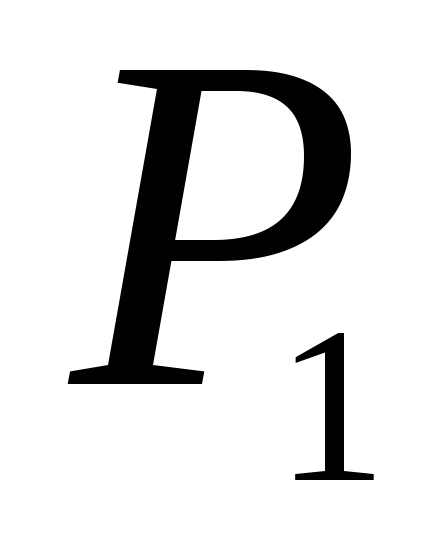 ;
2)
;
2)
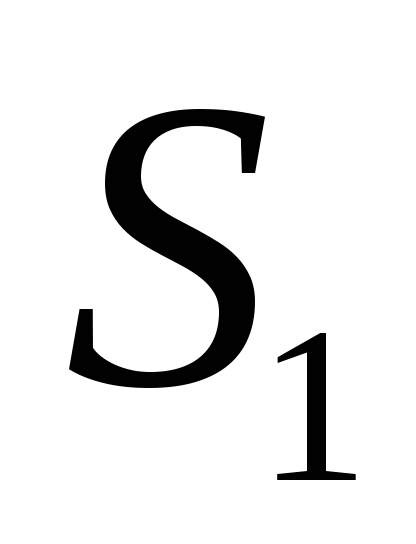 ,
,
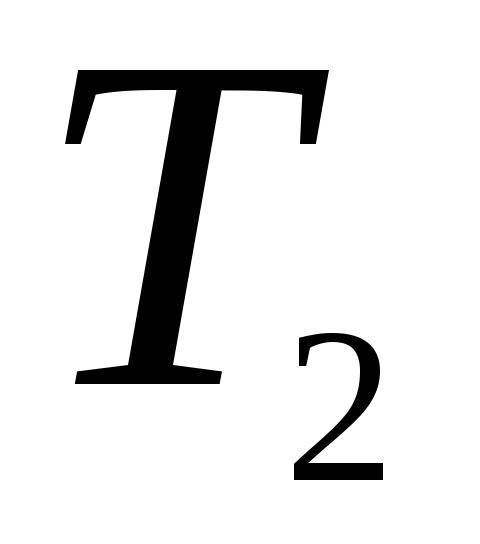 ,
3)
,
3)
 ,
,
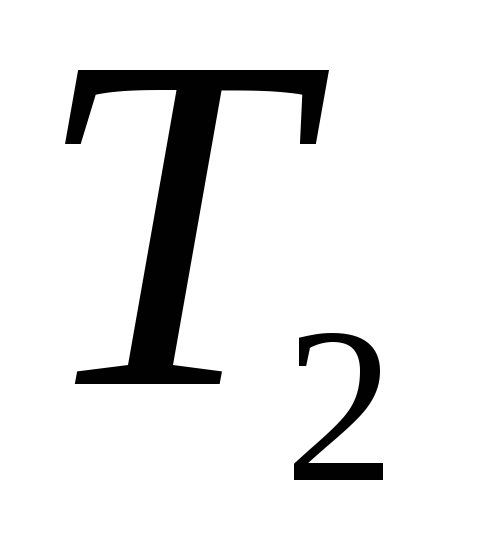 ,
,
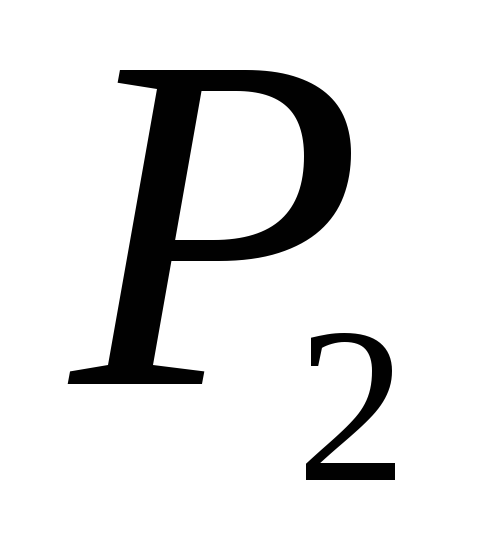 ;
4)
;
4)
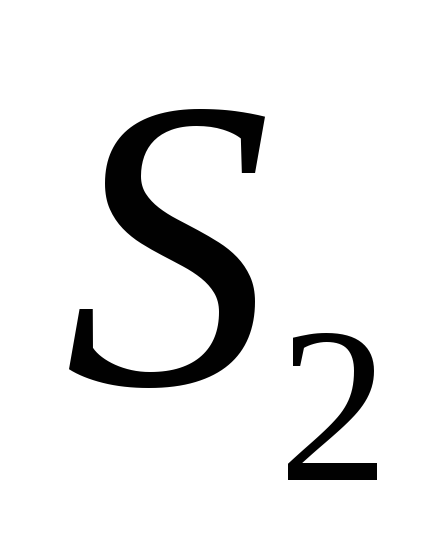 ,
,
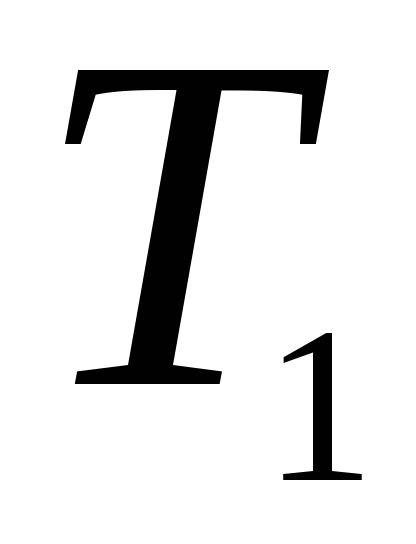 ;
5)
;
5)
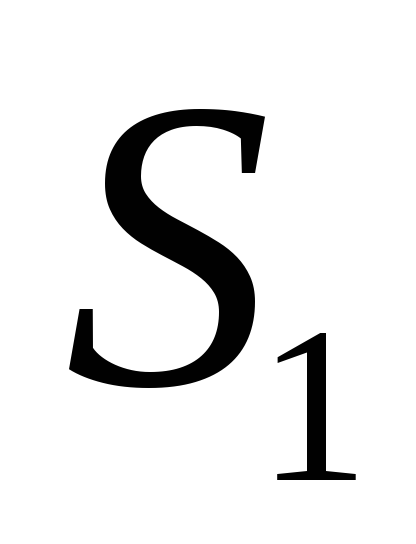 ,
,
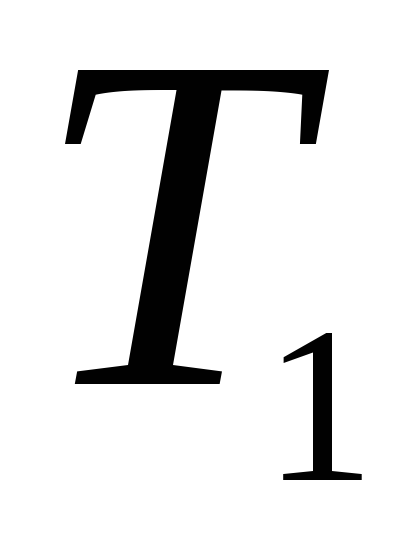 ,
,
 ).
).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им, для цикла из двух изобарных и двух изотермических процессов (последовательные состояния: 1)
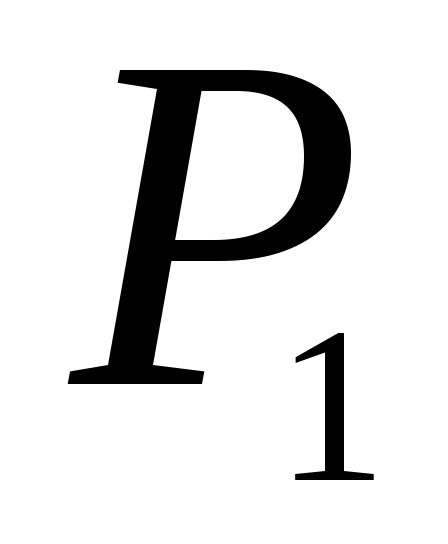 ,
,
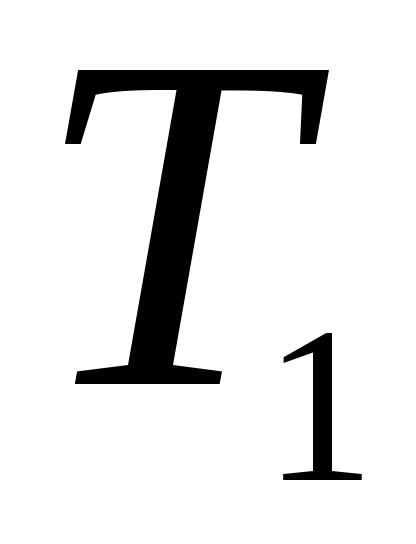 ;
2)
;
2)
 ,
,
 ;
3)
;
3)
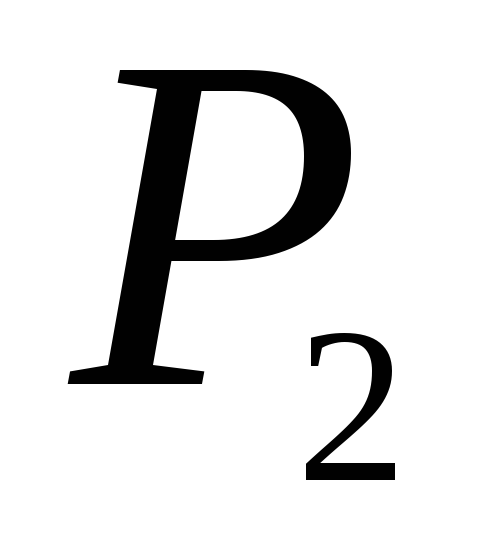 ,
,
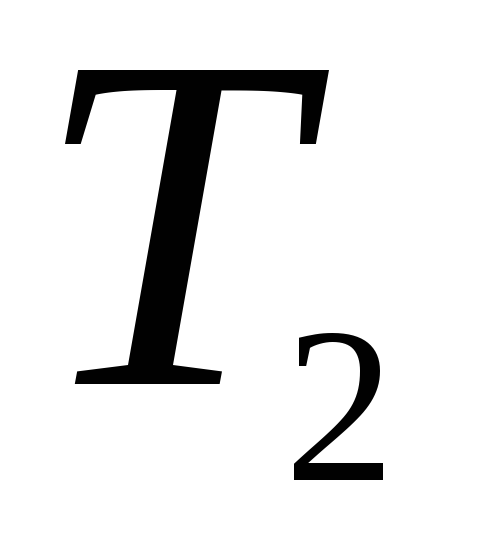 ;
4)
;
4)
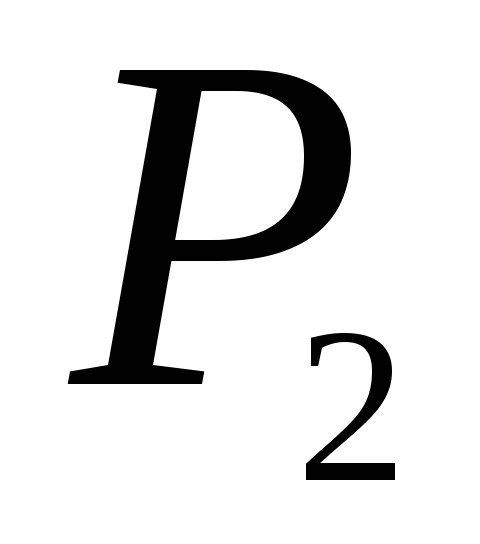 ,
,
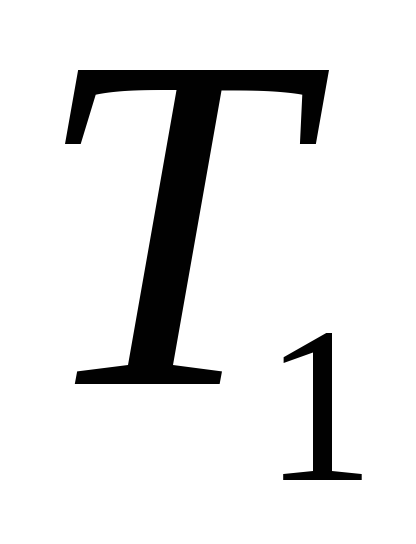 ;
5)
;
5)
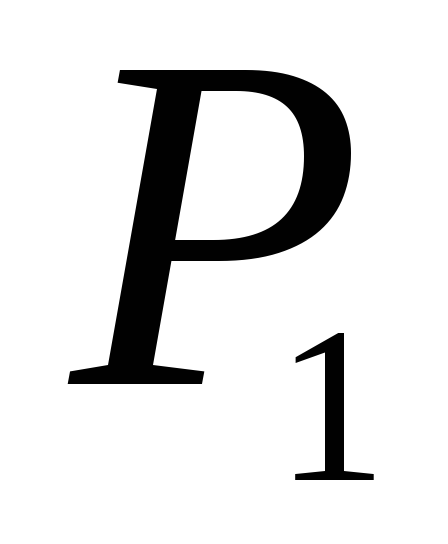 ,
,
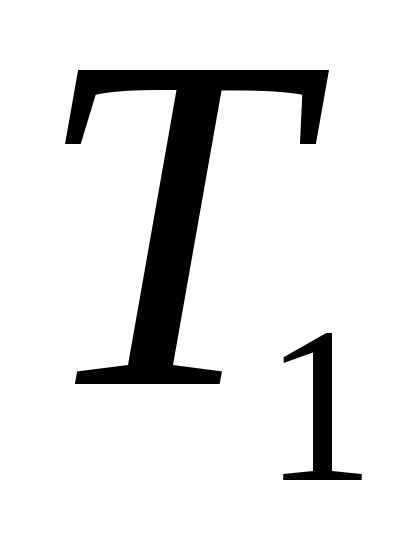 ).
).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им, для цикла из двух изобарных и двух адиабатических процессов (последовательное состояние газа: 1)
 ,
,
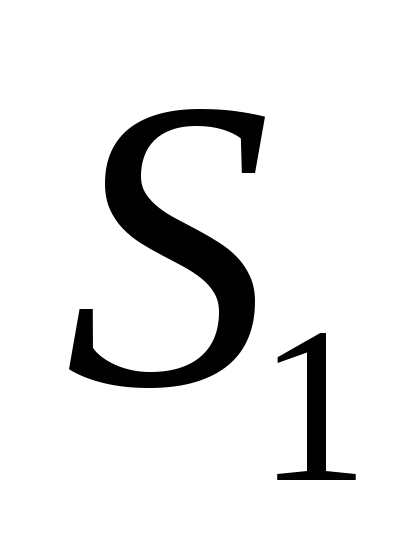 ,
,
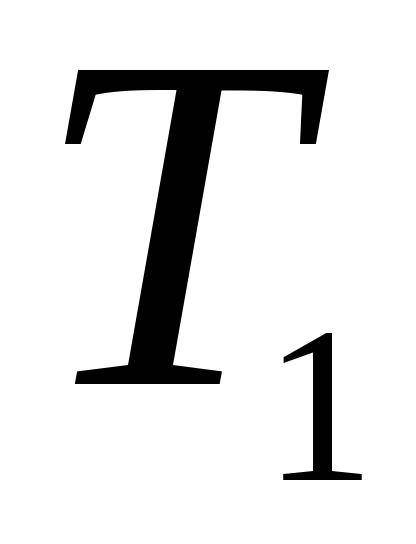 ;
2)
;
2)
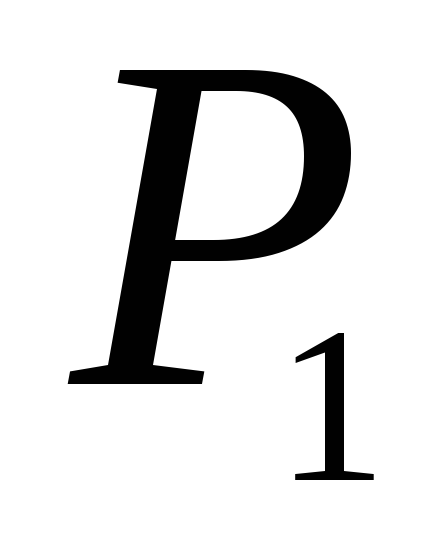 ,
,
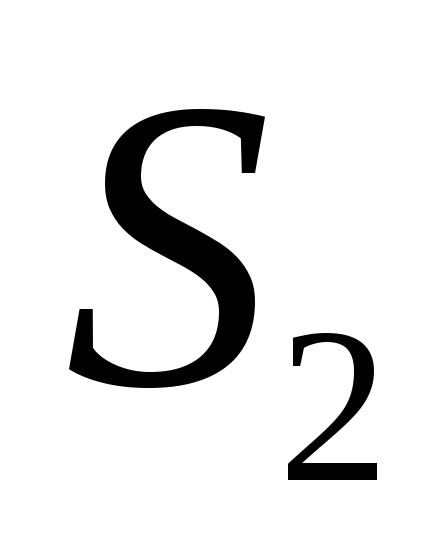 ;
3)
;
3)
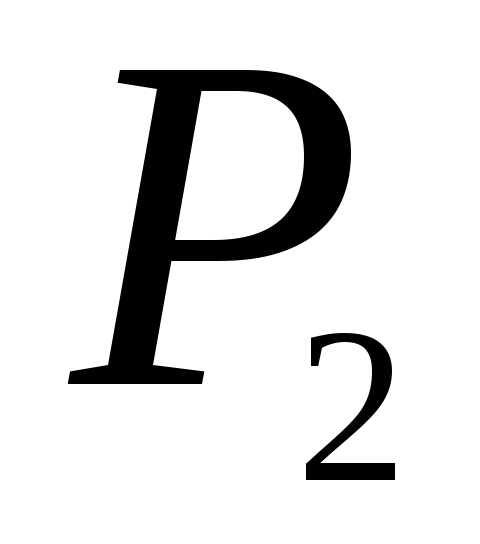 ,
,
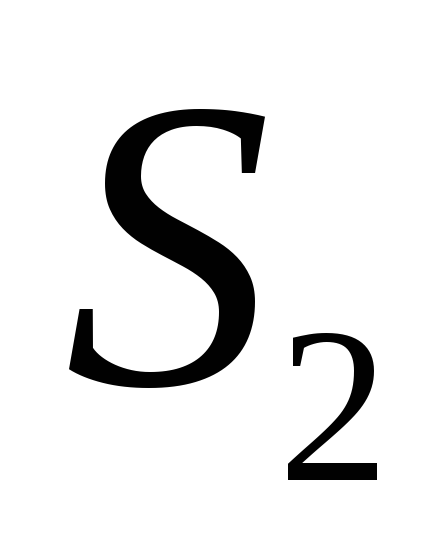 ,
,
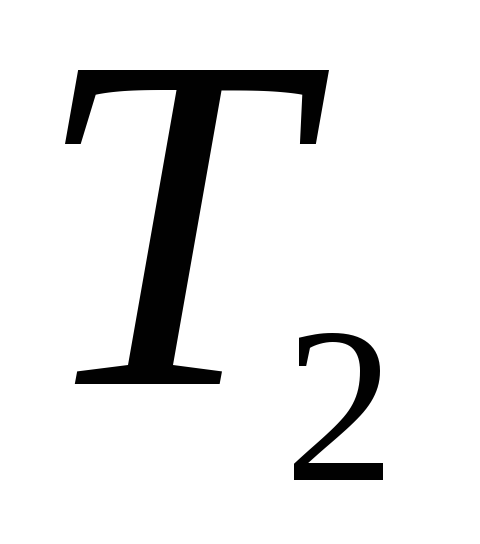 ;
4)
;
4)
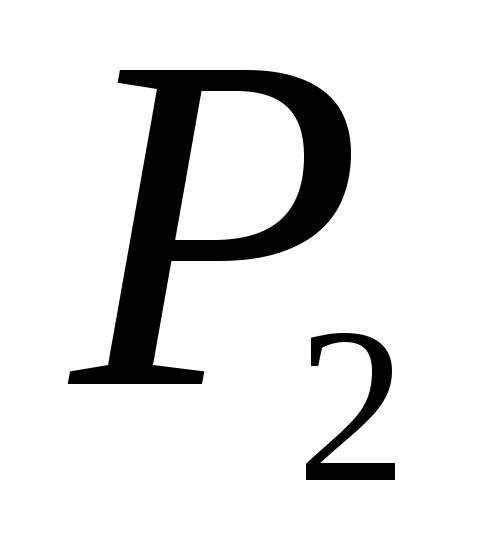 ,
,
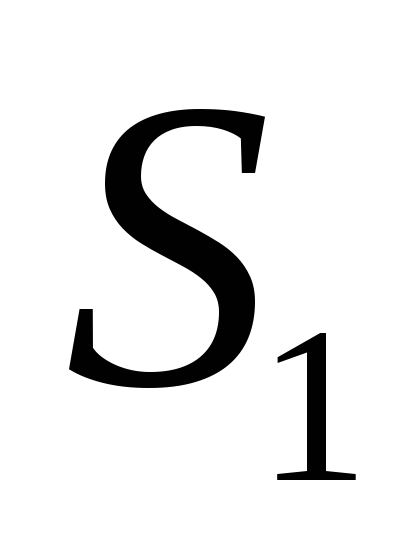 ;
5)
;
5)
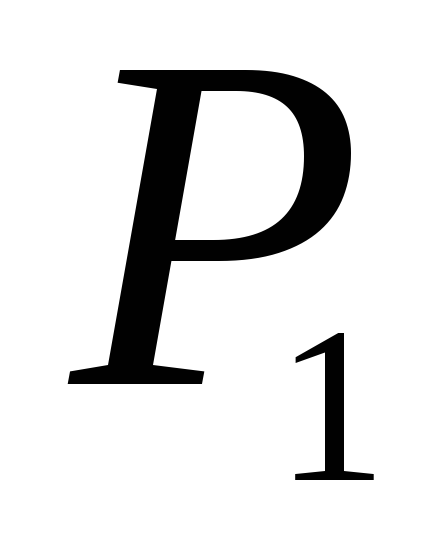 ,
,
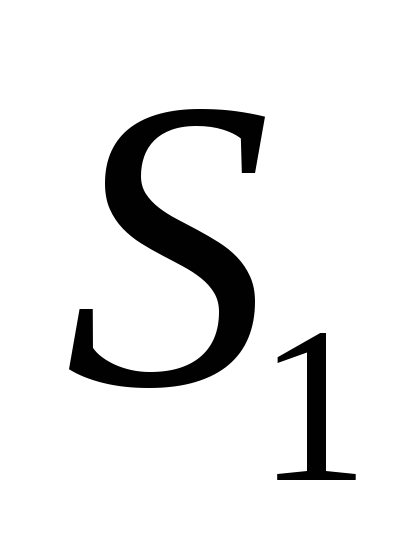 ,
,
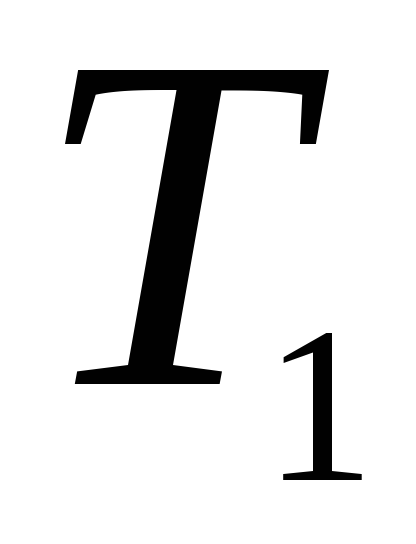 ).
).
-
Найти работу, производимую над идеальным газом, и количество тепла, получаемое им, для цикла из двух изохорных и двух адиабатических процессов (последовательные состояния: 1)
 ,
,
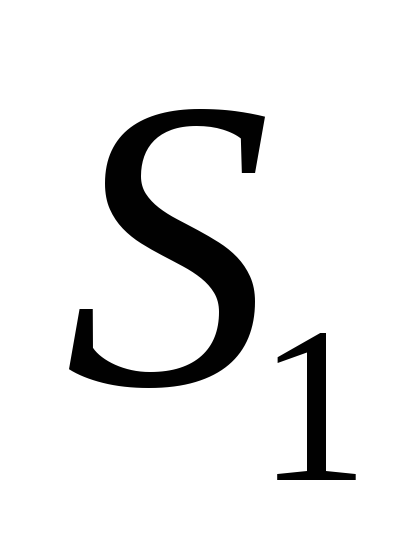 ,
,
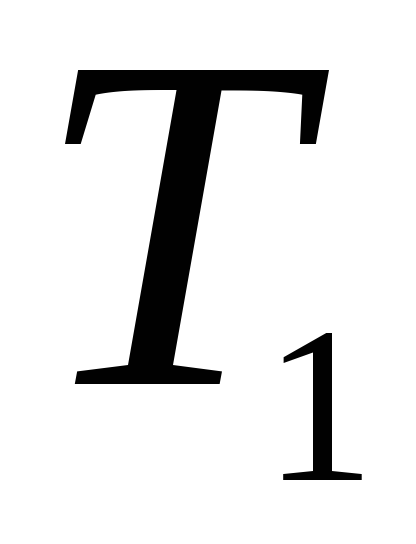 ;
2)
;
2)
 ,
,
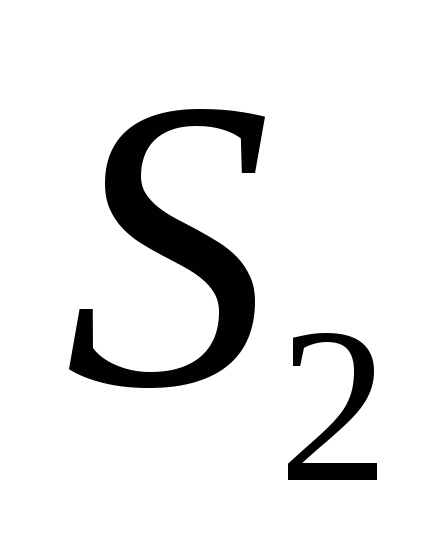 ;
3)
;
3)
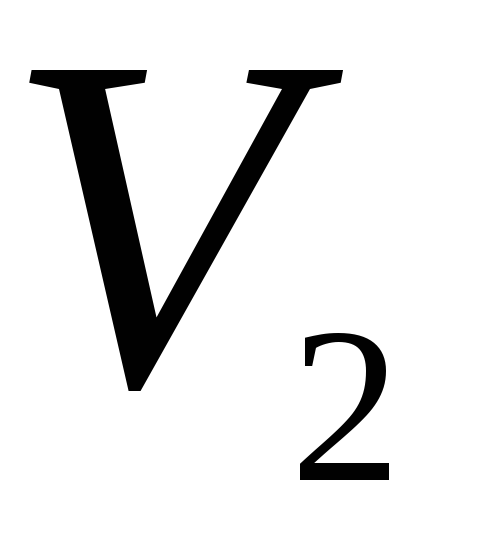 ,
,
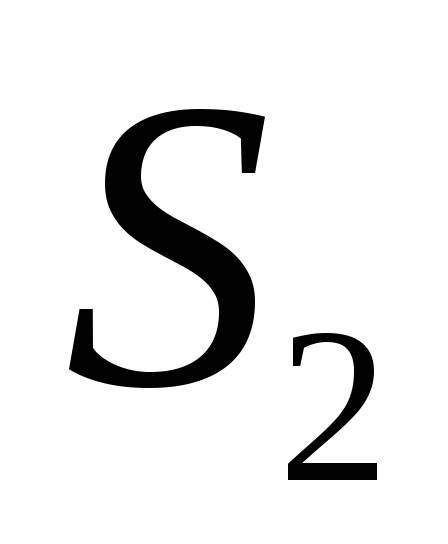 ,
,
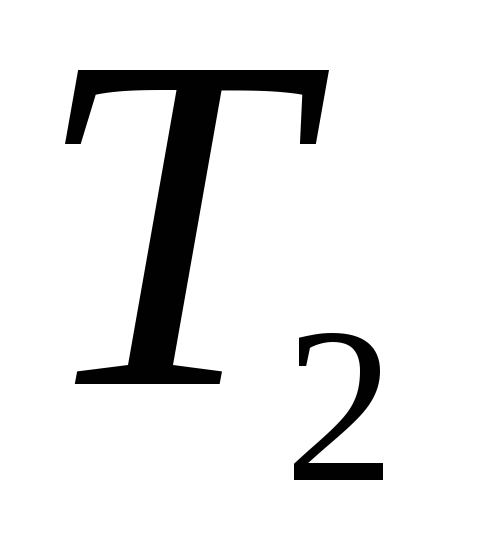 ;
4)
;
4)
 ,
,
 ;
5) )
;
5) )
 ,
,
 ,
,
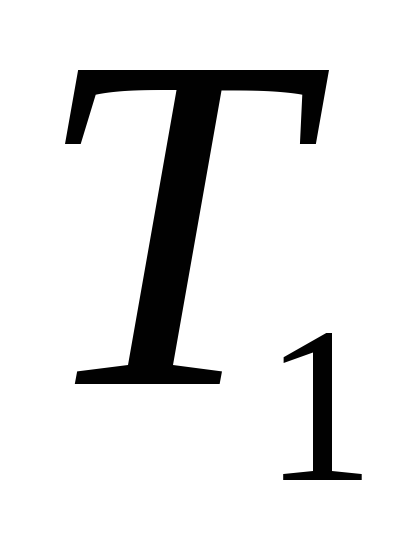 ).
).
-
Определить максимальную работу, которую можно получить при соединении сосудов с двумя одинаковыми идеальными газами, имеющими одинаковые температуру
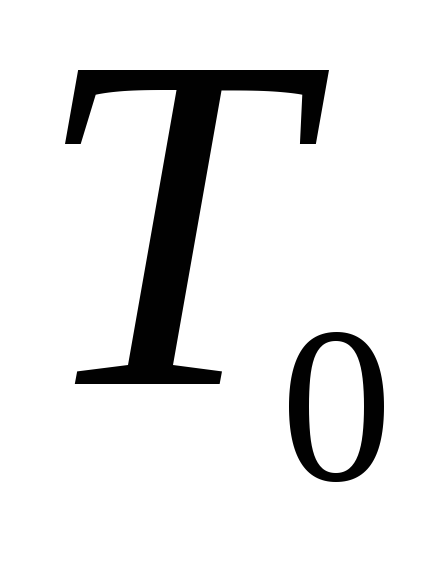 и число частиц
и число частиц
 ,
но разные объемы
,
но разные объемы
 и
и
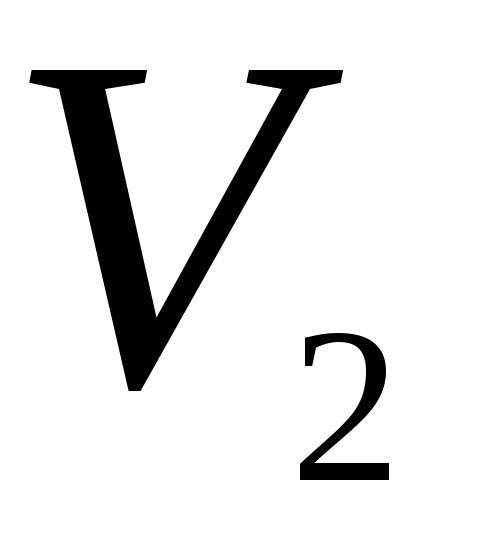 .
.
-
Определить максимальную работу, которую можно получить при соединении сосудов с двумя одинаковыми идеальными газами, если до соединения сосудов газы имели одинаковое давление
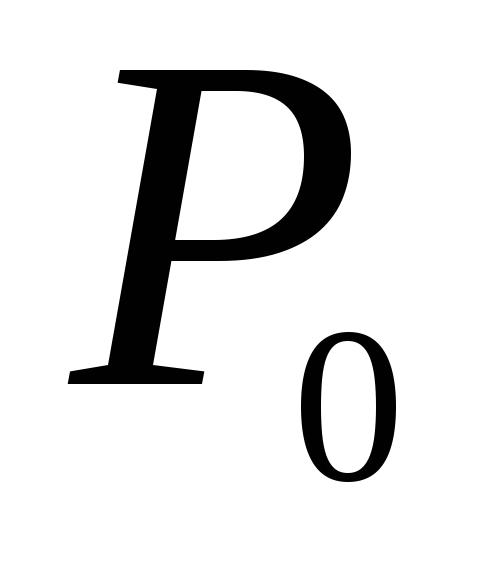 и разные температуры
и разные температуры
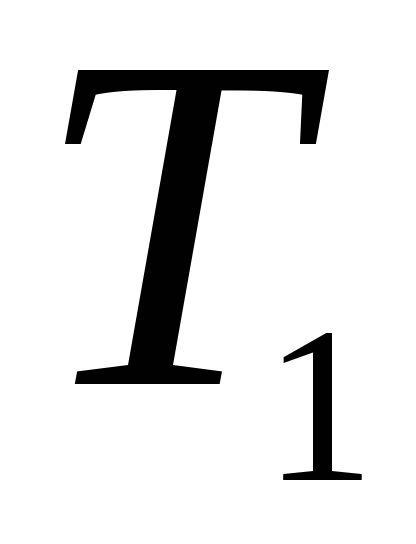 и
и
 .
.
-
Найти минимальную работу, которую надо произвести над идеальным газом для того, чтобы сжать его от давления
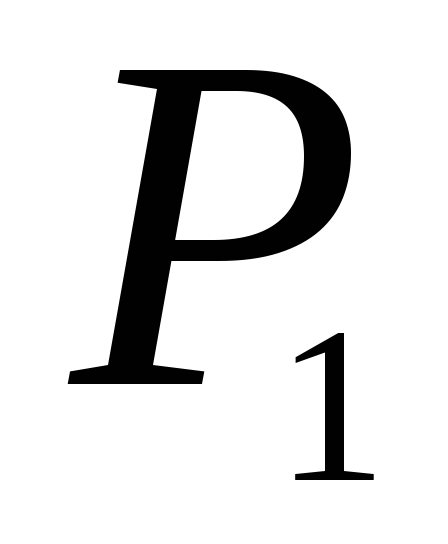 до давления
до давления
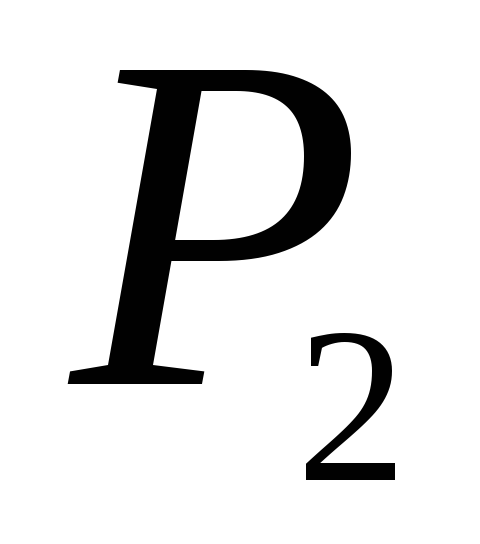 при постоянной температуре среды (
при постоянной температуре среды (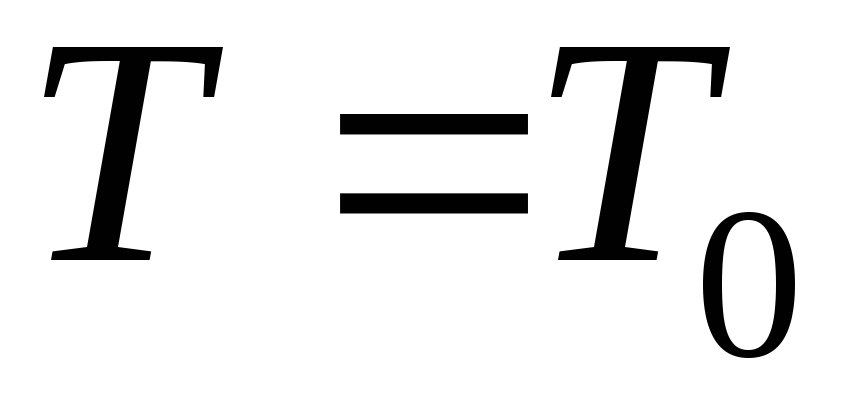 ).
).
-
Определить максимальную работу, которую можно получить с помощью идеального газа при охлаждении от температуры
 до температуры среды
до температуры среды
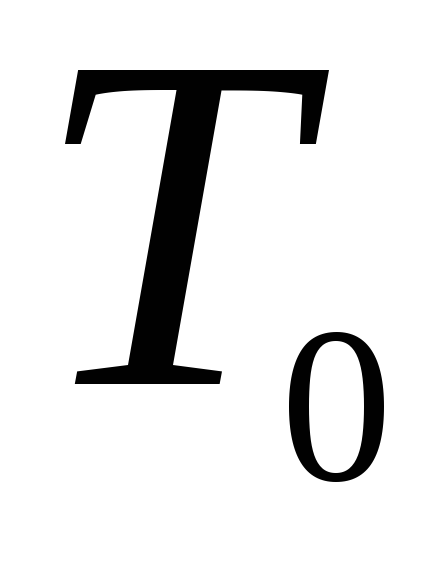 при постоянном объеме.
при постоянном объеме.
-
Определить максимальную работу, которую можно получить с помощью газа, охлаждающегося от температуры
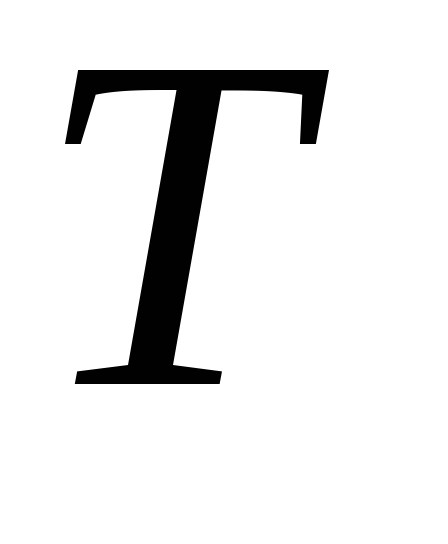 до температуры среды
до температуры среды
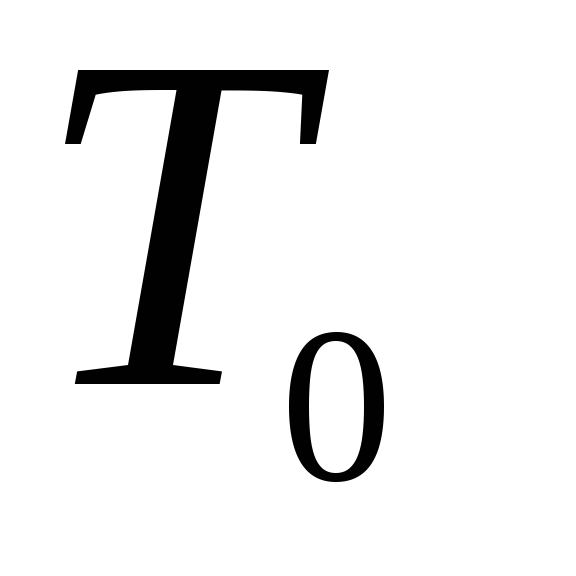 и
в то же время расширяющегося так, что
его давление меняется от
и
в то же время расширяющегося так, что
его давление меняется от
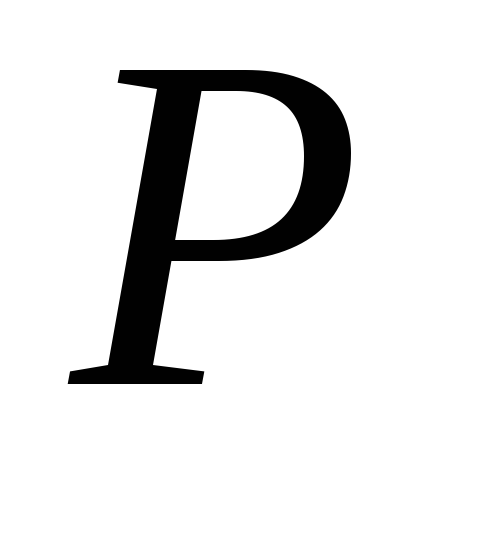 до давления среды
до давления среды
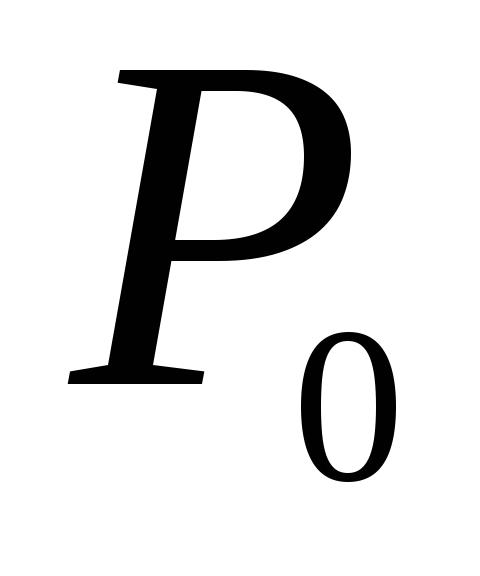 .
.
-
Найти
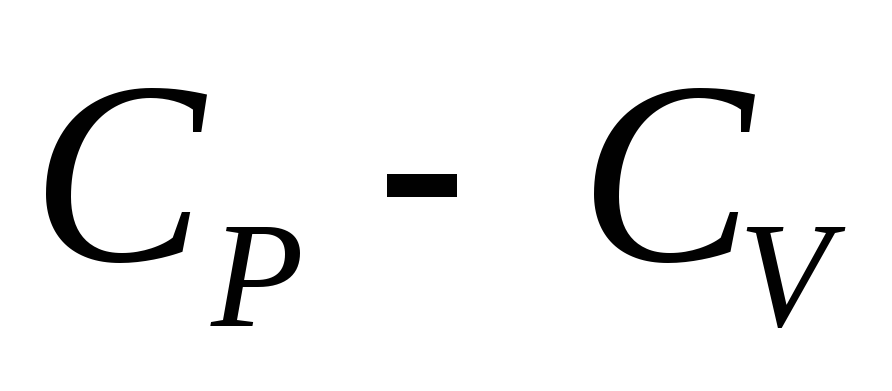 для неидеального газа, описывемого
уравнением Пенга-Робинсона..
для неидеального газа, описывемого
уравнением Пенга-Робинсона..
-
Найти уравнение адиабатического процесса для газа ван-дер-Ваальса с постоянной теплоемкостью
 .
.
-
Найти изменение температуры для газа ван-дер-Ваальса с постоянной теплоемкостью
 при расширении этого газа в пустоту.
при расширении этого газа в пустоту.
-
Найти зависимость точки инверсии процесса Джоуля – Томсона от температуры для газа ван-дер-Ваальса с постоянной теплоемкостью
 .
.
-
Найти параметры
 и
и
 уравнения Пенга-Робинсона для метана.
Критические параметры метана равны
уравнения Пенга-Робинсона для метана.
Критические параметры метана равны
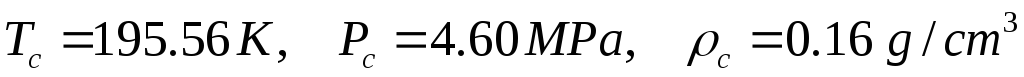
-
Найти параметры
 и
и
 уравнения Пенга-Робинсона для этана.
Критические параметры этана равны
уравнения Пенга-Робинсона для этана.
Критические параметры этана равны
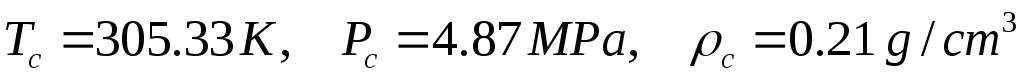
25. Найти параметры
![]() и
и
![]() уравнения Пенга-Робинсона для пропана.
Критические параметры пропана равны
уравнения Пенга-Робинсона для пропана.
Критические параметры пропана равны
![]()
28. Пусть газ подчиняется уравнению
состояния ван-дер-Ваальса
![]() а его молярная теплоемкость при
постоянном объеме
а его молярная теплоемкость при
постоянном объеме
![]() постоянна и не зависит от температуры.
Показать, что внутренняя энергия (на 1
моль) такого газа
постоянна и не зависит от температуры.
Показать, что внутренняя энергия (на 1
моль) такого газа
![]() определяется выражением
определяется выражением
![]()
и что при адиабатическом квазистатическом изменении выполняется соотношение
![]() или
или
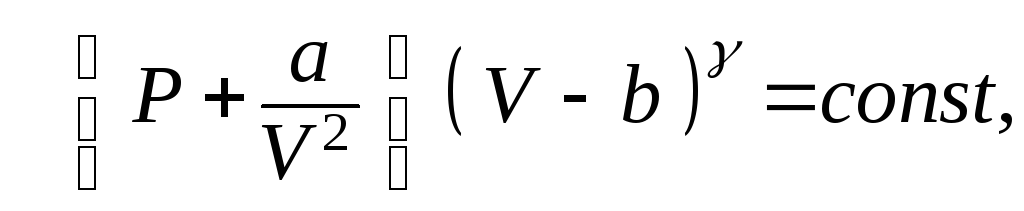
где
![]() Кроме того, найти изменение температуры
этого газа при его свободном расширении
в вакуум.
Кроме того, найти изменение температуры
этого газа при его свободном расширении
в вакуум.
29. Доказать, что у газа ван-дер-Ваальса теплоемкость при постоянном объеме зависит только от температуры, и найти выражение для внутренней энергии и энтропии.
30. Пусть для некоторого твердого тела
экспериментально найдено, что при
температуре
![]() в интервале давлений
в интервале давлений
![]() имеет место следующая зависимость:
имеет место следующая зависимость:

Насколько возрастет энтропия при сжатии
тела от давления
![]() до
до
![]() при постоянной температуре
при постоянной температуре
![]()
31. Доказать выражения для к.п.д. цикла Отто (рабочим веществом является идеальный газ):

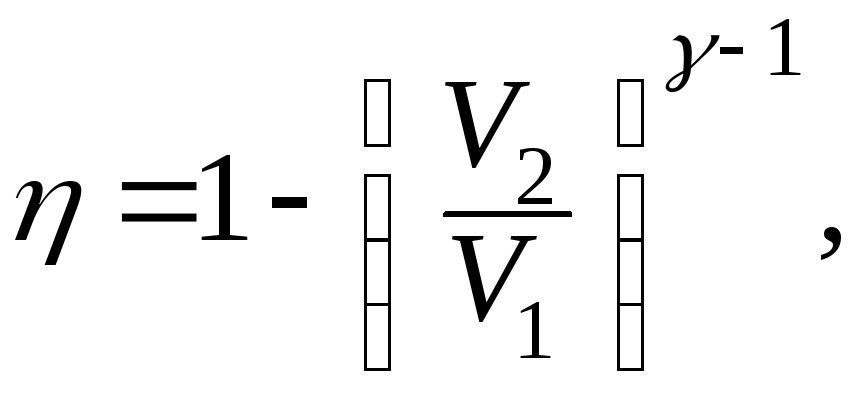
32. Доказать выражения для к.п.д. цикла Джоуля (рабочим веществом является идеальный газ):
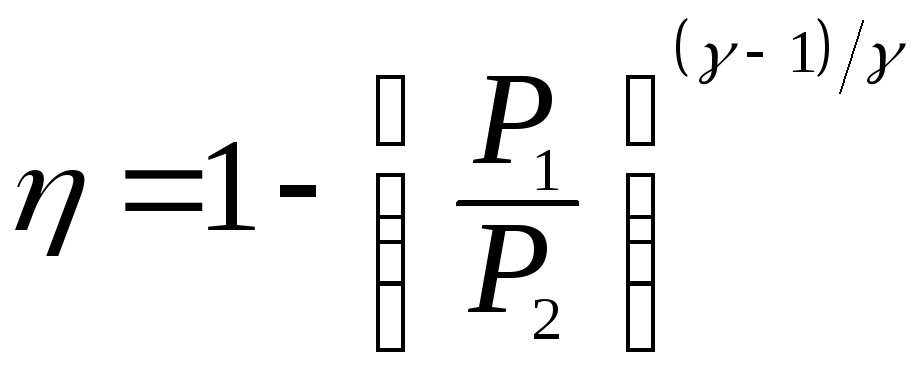

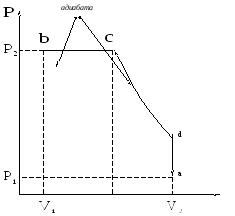
33. Доказать выражения для к.п.д. цикла Дизеля (рабочим веществом является идеальный газ):
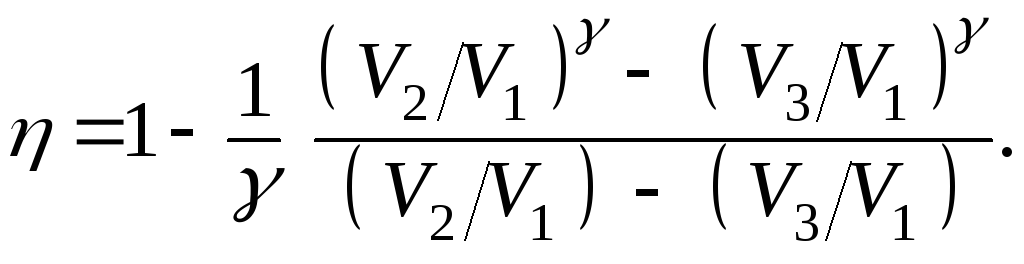
П ри
этом считать, что
ри
этом считать, что
![]() и
и
![]() константы.
константы.
34
Имеется
пружина, подчиняющаяся закону Гука: при
постоянной температуре
![]() .
.
Найти свободную энергию,
внутреннюю энергию и энтропию, как
функции удлинения
![]() .
.
35
Натяжение резиновой ленты, растянутой
до длины
![]() равно
равно
![]() .
.
Показать, что внутренняя энергия такой ленты зависит только от температуры, а ее энтропия уменьшается с увеличением длины.
36 Показать, что при адиабатическом растяжении описанной в предыдущей задаче ленты температура повышается. Показать, что лента будет сжиматься, если повышать температуру , оставляя натяжение постоянным.
37
Парамагнитное тело имеет изотермическую
восприимчивость
![]() .
Найти плотность свободной энергии,
внутренней энергии и энтропии.
.
Найти плотность свободной энергии,
внутренней энергии и энтропии.
38 Из выражений для свободной энергии в
переменных
![]() получить выражение для свободной энергии
в переменных
получить выражение для свободной энергии
в переменных
![]()
39 Показать, что для адиабатического
изменения абсолютной температуры
![]() магнетика, подчиняющегося закону Кюри
магнетика, подчиняющегося закону Кюри
![]() (
(![]() намагниченность,
намагниченность,![]() ,
,
![]() константа),
справедливо соотношение.
константа),
справедливо соотношение.
![]()
где
![]() теплоемкость на единицу объема при
постоянном магнитном поле.
теплоемкость на единицу объема при
постоянном магнитном поле.
40 Магнитная восприимчивость парамагнитного
вещества подчиняется закону Кюри
![]() (
(![]() константа), а внутренняя энергия
определяется выражением
константа), а внутренняя энергия
определяется выражением
![]() (
(![]() положительная константа).
положительная константа).
А). Найти теплоту намагничивания, когда
поле возрастает от
![]() до
до
![]() температура сохраняет постоянное
значение
температура сохраняет постоянное
значение
![]()
б) Как меняется температура при
адиабатическом размагничивании, т.е.
при адиабатическом уменьшении поля от
![]() до
до
![]()
-
Минимальная работа по отклонению системы от равновесного состояния равна
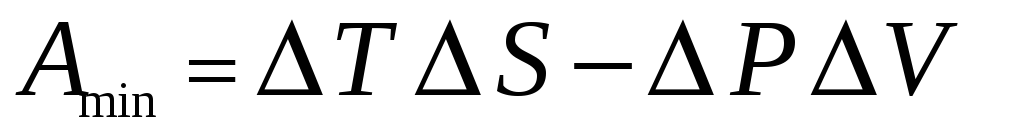 .
Исходя из этого выражения, найти
средний квадрат флуктуций объема
подсистемы.
.
Исходя из этого выражения, найти
средний квадрат флуктуций объема
подсистемы.
-
Минимальная работа по отклонению системы от равновесного состояния равна
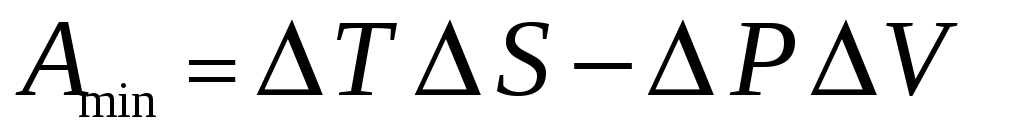 .
Исходя из этого выражения, найти
средний квадрат флуктуций температуры.
.
Исходя из этого выражения, найти
средний квадрат флуктуций температуры.
-
Минимальная работа по отклонению системы от равновесного состояния равна
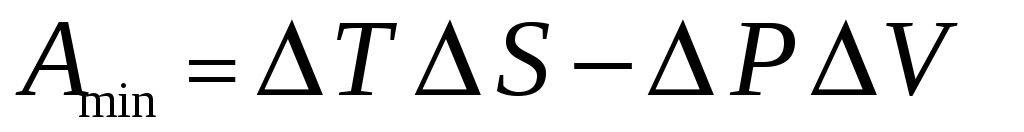 .
Исходя из этого выражения, найти
средний квадрат флуктуций энергии
(пользуясь в качестве независимых
переменных
.
Исходя из этого выражения, найти
средний квадрат флуктуций энергии
(пользуясь в качестве независимых
переменных
 и
и
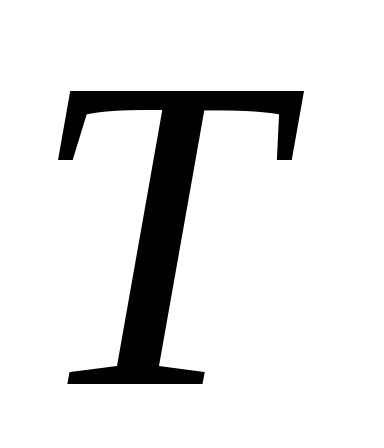 .
.
-
Минимальная работа по отклонению системы от равновесного состояния равна
 .
Исходя из этого выражения,
найти среднее от произведения <
.
Исходя из этого выражения,
найти среднее от произведения <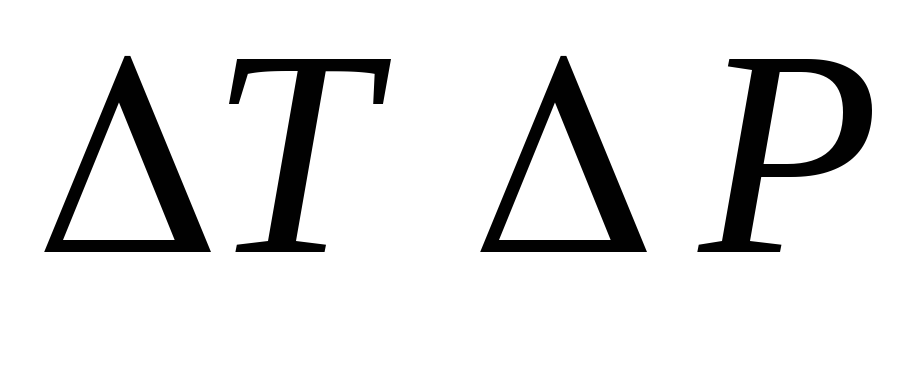 >.
>.
-
Минимальная работа по отклонению маятника от равновесного положения равна
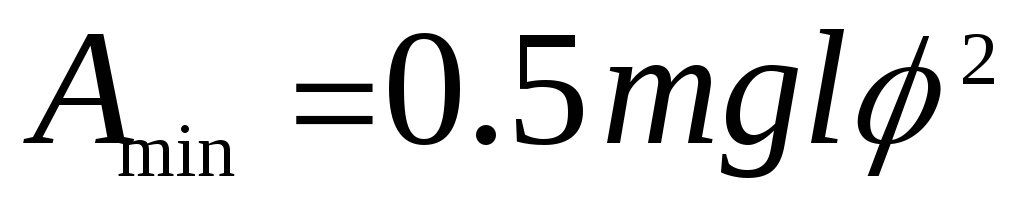 ,
где
,
где
 - угол отклонения от вертикали. Исходя
из этого выражения, найти средний
квадрат флуктуационного отклонения
маятника от вертикали.
- угол отклонения от вертикали. Исходя
из этого выражения, найти средний
квадрат флуктуационного отклонения
маятника от вертикали.
