by norman (KSS)

КОНТРОЛЬНЫЕ ВОПРОСЫ ПО СТАТИКЕ

(Первый коллоквиум)

1. Сформулируйте аксиомы статики.

1-ая: Если на свободное абсолютно твёрдое тело действует две силы, то эти силы эквивалентны нулю тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны.

2-ая: Действие данной системы сил на абсолютно твёрдое тело не изменится, если к ней присоединить или от неё отнять систему, эквивалентную нулю.

3-тья: Всякому действию одного материального тела на другое всегда соответствует равное по величине, но противоположно направленное противодействие.

4-ая: Две силы, приложенные к одной точке твёрдого тела, имеют равнодействующую, приложенную к той же точке и изображаемую диагональю параллелограмма, построенного на данных силах как на сторонах.

5-ая: (аксиома связей): всё то, что ограничивает свободу перемещения данного тела в пространстве, называется связью. Сила, с которой данная связь действует на тело, препятствую тем или иным его перемещениям, называется силой реакции связи, или просто реакцией связи. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие силами реакции этих связей.

6-ая: (принцип отвердиваемости): если изменяемое (деформируемое) тело находиться под действием некоторой системы сил в равновесии, то равновесие не нарушиться и в том случае, если это тело отвердеет (т.е. станет абсолютно твёрдым).

2. Дайте определения равнодействующей и уравновешивающей произвольной системы сил.

- Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.

- Силой, уравновешивающей систему сил, называют такую силу, которая, будучи присоединенной к данной системе сил, составляет вместе с ней новую систему сил, эквивалентную нулю.

3. Какая система сил называется сходящейся?

Система сил, расположенных в пространстве так, что линии из действия пересекаются в одной точке, называется системой сходящихся сил.

4. Как определить равнодействующую системы сходящихся сил?

- Считая, что вектор силы скользящий, перенесем все силы данной системы вдоль линий действия в точку их пересечения и попарно сложим все силы методом параллелограмма.

- Последовательно прикладываем вектора сил данной системы в конечную точку каждого последующего вектора, сохраняя его величину и направление, затем, соединив начало вектора 1 с концом вектора N, получим равнодействующую системы сходящихся сил. Такой метод называют методом силового много угольника.

- Система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линии действия всех сил и равна их геометрической сумме.

5. Запишите и сформулируйте условия равновесия системы сходящихся сил в векторной форме, а также в проекциях на оси декартовой системы координат.

Условия равновесия в векторной форме

- Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этой системы сил равнялась нулю.

- Если - вектор, замыкающий силовой многоугольник: геометрической условие равновесия системы сходящихся сил означает, что силовой многоугольник, построенный на векторах слагаемых сил данной системы, замкнут.

Условия равновесия в аналитической форме

- , т.е. , , . Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из трёх выбранных любым образом координатных осей равнялись нулю.

- , . Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекция всех сил на каждую из двух выбранных любым образом координатных осей, лежащих в плоскости действия данной системы, равнялись нулю.

6. Сформулируйте теорему о трех уравновешенных силах.

Если под действием трёх сил тело находиться в равновесии, и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пресекаются в одной точке.

7. Дайте определение алгебраической величины момента силы относительно некоторого центра.

Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.

8. Запишите векторное выражение момента силы относительно некоторого центра.

Момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на вектор силы.

9. Почему для плоской системы сил нет необходимости придавать векторный смысл моменту силы?

- В случае плоской системы сил момент силы относительно точки можно принимать за алгебраическую величину.

- Для пространственной системы сил, момент – это вектор, который направлен перпендикулярно к плоскости, в которой лежат сила и точка, в ту сторону, откуда вращение тела силой представляется происходящим против хода часовой стрелки.

10. Дайте определение момента силы относительно оси и укажите способы его нахождения.

- Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью.

- Момент силы относительно оси равен проекции на эту ось вектора момента силы относительно произвольной точки, лежащей на этой оси.

- Если сила задана своими проекциями и координатами x, y, z точки приложения, то момент силы относительно начала координат может быть представлен в виде определителя третьего порядка:

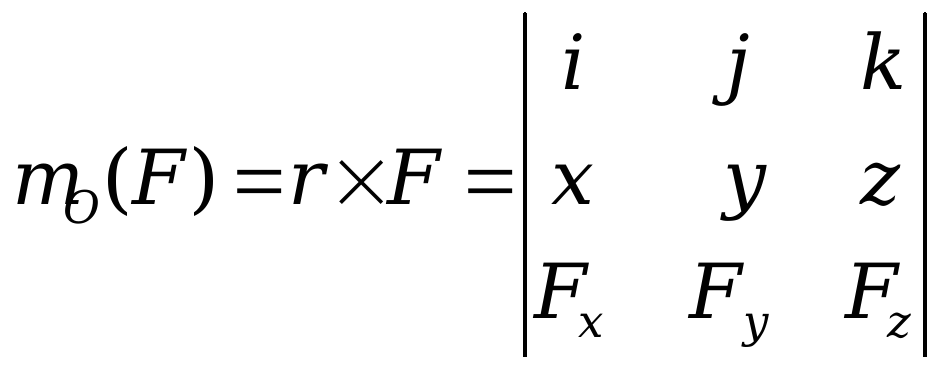
- для определения знака момента, удобно рассматривать систему с положительных направления осей x, y, z и принимать момент положительным, если проекция силы на плоскость, перпендикулярную оси пытается создать вращательный эффект вокруг этой же оси против хода часовой стрелки.

11. В каких случаях момент силы относительно оси равен нулю?

Момент силы относительно оси равен нулю, когда линия действия силы параллельная оси или пересекает её.

12. Какова связь между моментом силы относительно оси и моментом силы относительно любой точки, лежащей на этой оси.

А – точка приложения силы, АВ – направления вектора силы, O – моментная точка, начало координат.

13. Дайте определение пары сил.

Система двух равных по величине, антипараллельных и не лежащих на одной прямой сил, называется парой. Пара не имеет равнодействующей, то есть не может быть заменена одной эквивалентной ей силой.

14. Дайте определения момента пары сил. Как направлен вектор-момент пары.

- Численное значение момента пары равно произведению величины одной из сил пары на плечо этой пары.

- Сумма моментов сил пары относительно любого центра равна моменту пары.

- Момент пары есть вектор, перпендикулярный к плоскости действия пары, направленный в сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки.

15. Сформулируйте теоремы об эквивалентности и сложении пар.

Т1: Действие пары на абсолютно твёрдое тело не измениться, если пару переместить в другое положение в плоскости ее действия.

Т2: действие пары на абсолютно твёрдое тело не измениться, если ее перенести а любую плоскость, параллельную плоскости действия данной пары.

Т3: Действие пары на абсолютно твёрдое тело не измениться, если любым способом видоизменить модули сил и плечо пары, сохраняя постоянным их произведение, т.е. момент пары.

Т4: система пар, действующих на абсолютно твёрдое тело, эквивалентна одной паре, вектор-момент которой равен геометрической сумме моментов слагаемых пар.

16. Сформулируйте лемму о параллельном переносе силы.

Всякая сила, приложенная к абсолютно твёрдому телу в данной точке А, эквивалентна той же силе, приложенной в любой другой точке В и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.

17. Дайте определение главного вектора и главного момента произвольной пространственной системы сил.

- Сила , равная геометрической сумме всех сил данной системы, называется главным вектором.

- Величина , равная геометрической сумме моментов всех сил системы относительно центра приведения, называется главным моментом относительно этого центра.

18. Чем отличается главный вектор от равнодействующей произвольной системы сил.

Вектор есть главный вектор данной системы сил, а не равнодействующая этой системы, так как главный вектор не эквивалентен исходной системе сил. Главный вектор является равнодействующей приведенной системы сил, а не исходной.

19. Напишите аналитические выражения для главного вектора и главного момента.

Векторное: и

Аналитическое: ; ;

; ;

20. Объяснить, как взаимно расположены главный вектор и главный момент произвольной плоской системы сил.

- Величины, которые не изменяются при каком-либо преобразовании, называются инвариантами по отношению к этим преобразованиям.

- Величина и направление главного вектора не зависит от выбора центра приведения.

- первый инвариант

- Скалярное произведение главного момента произвольной пространственной системы сил на главный вектор той же системы не зависит от выбора центра приведения и является вторым инвариантом.