§1.4 Уравнения шредингера. Простейшие случаи движения микрочастиц

Положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции (пси – функции) . ВероятностьdР того, что частица находится в элементе объема dV, пропорциональна и элементу объемаdV

. (1.28)

Величина естьплотность вероятности ρ и задает вероятность пребывания частицы в данной точке пространства

. (1.29)

Кроме того, величиной определяется интенсивность волны де Бройля, аналогично интенсивности световой волны.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

< 1 (1.30)

При этом в бесконечном объёме Р = 1, т.е. вероятность найти частицу в бесконечном объеме максимальна.

Условие нормировки вероятностей и самой ψ - функции

. (1.31)

Данное условие указывает на объективное существование частицы во времени и пространстве.

Волновая функция должна удовлетворять ряду ограничительных условий. Она должна быть:

• конечной (вероятность не может быть больше единицы);

• однозначной (вероятность не может быть неоднозначной величиной);

• непрерывной (вероятность не может изменяться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных квантовых состояниях, описываемых волновыми функциями , то она также может находиться в состоянии , описываемом линейной комбинацией этих функций

, (1.32)

где C_n (n=1,2,…) – произвольные комплексные числа.

Волновая функция, описывающая одномерное движение свободной частицы, фактически это есть волновая функция для плоской волны.

(1.33)

где А  амплитуда волны де Бройля; р  импульс частицы; Е  энергия час­тицы

Вероятность dР обнаружить частицу в интервале от x до x+dx (в одномерном случае) выражается формулой

dР=. (1.34)

Вероятность Р обнаружить частицу в интервале от x₁ до x₂ находится ин­тегрированием dР в указанных пределах

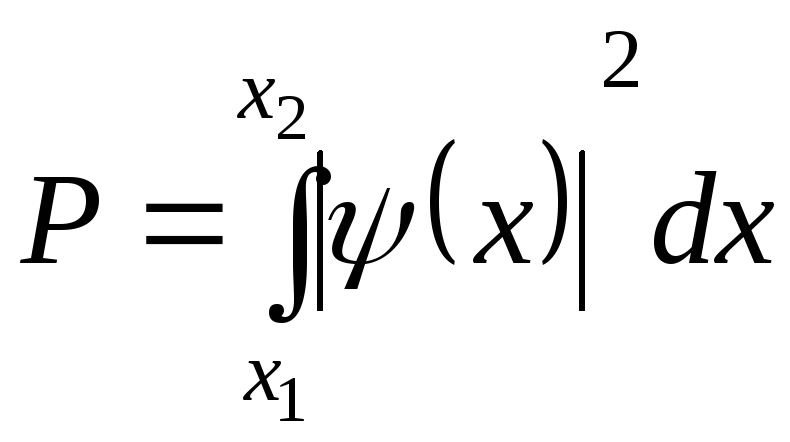. (1.35)

Уравнение Шредингера

Временным уравнением Шредингера называется основное дифференциальное уравнение квантовой механики относительно волновой функции . Оно определяет-функцию для микрочастиц, движущихся в силовом поле с потенциальной энергиейU (x,y,z,t) со скоростью <c, где с – скорость света в вакууме. Уравнение Шредингера имеет вид

, (1.36)

где i  мнимая единица (),m  масса частицы,  модифицированная постоянная Планка, - оператор Лапласа ()

Одномерное временное уравнение Шредингера

i=-. (1.37)

Уравнение Шредингера дополняется условиями, которые накладываются на - функцию:

а) функция должна быть конечной, однозначной и непрерывной;

б) производные должны быть непрерывны;

в) функция должна быть интегрируема, т.е. интегралдолжен быть конечным. Это условие в простейших случаях сводится к условию нормировки вероятностей.

В случае, когда -функция не зависит от времени , она удовлетворяетстационарному уравнению Шредингера

, (1.38)

где Е  полная энергия частицы.