Корпускулярно – волновая двойственность свойств света

Рассмотренные выше закономерности равновесного теплового излучения, фотоэффект, эффект Комптона – служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов. С другой стороны, такие явления, как интерференция, дифракция и поляризация света, подтверждают волновую (электромагнитную) природу света. Однако волновой и квантовый способы описания света не противоречат, а взаимно дополняют друг друга, так как свет одновременно обладает и волновыми и корпускулярными свойствами.

Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики – энергия Е и импульс р, а с другой волновые характеристики – частота ν и длина волны λ. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов

, . (1.23)

Смелость гипотезы де Бройля заключалась в том, что данные соотношения были перенесены им на другие микрочастицы с массой покоя не равной нулю.

Все частицы, имеющие конечный импульс, обладают волновыми свойствами, и их движение сопровождается некоторым волновым процессом.

Формула де Бройля устанавливает зависимость длины волны, связанной с движущейся частицей вещества, от импульса частицы

, (1.24)

где m – масса частицы;

– ее скорость;

h = 6,625∙10^-34 Дж∙с – постоянная Планка.

Волны, о которых идет речь, называются волнами де Бройля.

Таблица 1. Аналогия формул корпускулярных и волновых свойств материи

Корпускулярные свойства	Волновые свойства
Скорость Энергия Е = mc2	Длина волны де Бройля Частота волны де Бройля Групповая скорость волн де Бройля u= Фазовая скорость волн де Бройля

Экспериментальное подтверждение гипотезы де Бройля: опыты с рассеянием и дифракцией электронов на монокристаллах. Формула для дифракции электронов на монокристаллах подобна формуле Вульфа-Брэггов для рентгеновских лучей

, (1.25)

где d – период решетки кристалла; φ – угол дифракции.

Соотношение неопределенностей Гейзенберга

В. Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927г. к выводу, что объект микромира невозможно одновременно с любой заданной точностью характеризовать и координатой, и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х , р_у, р_z), причем неопределенности этих величин удовлетворяют условиям

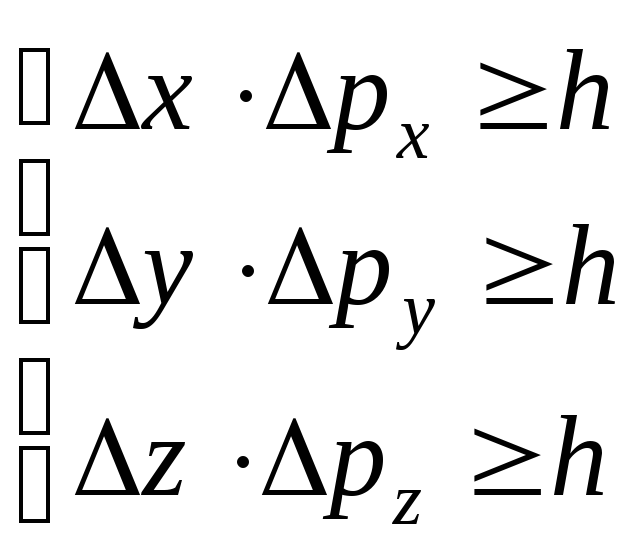(1.26)

Из соотношения неопределенностей (1.26) следует, что, например, если микрочастица находится в состоянии с точным значением координаты (Δх=0), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (Δр_х→ ∞), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.

В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t.

Смысл соотношений неопределенности для энергии и времени существенно отличается от смысла соотношений (1.26) координаты и импульса.

В (1.26) Δр и Δх – неопределенны в значениях импульса и координаты в один и тот же момент. Данное соотношение показывает, что эти две величины не могут иметь одновременно строго определенных значений. Энергия же Е, напротив, может быть измерена в каждый данный момент времени с любой точностью.

Т.е. неопределенности этих величин удовлетворяют условию

, (1.27)

где ∆Е – разность двух точно измеренных значений энергии в два различных момента времени, т.е. ∆Е – это совсем не есть неопределенность в значении энергии в определенный момент времени, а отвечает двум моментам времени измерения.

∆t – это время жизни системы в данном состоянии. Тогда , гдеЕ₁ – энергия, измеренная в начале жизни в данном состоянии, а Е₂ – в конце, т.е. ∆Е – изменение энергии за время жизни системы в заданном состоянии. Величина называется обычношириной (Г) данного уровня.

Из выражения (1.27) следует, что частота излученного фотона также должна иметь неопределенность , т.е. линии спектра должны характеризоваться частотой, равной. Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.