Подставим в (2.55) числовые значения, получим

n =1 ,

n =2 ,

n =3 .

Изобразим графически значения собственных волновых функций для электрона в потенциальной яме. Для этого удобно подставить значениях в долях l, например, x = 0; l/8; l/4; l/2; и т.д. (рис.12).

ЗАДАЧА №2.40 Электрон находится в бесконечно глубоком одномерном прямоуголь­ном потенциальном ящике шириной l. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (п=2), будет об­наружен в средней трети ящика.

Дано: х = l;

n = 2 ;

х = l.

Найти: Р -?

Решение

Вероятность Р обнаружить частицу в интервале x₁<x<x₂ определяется равенством

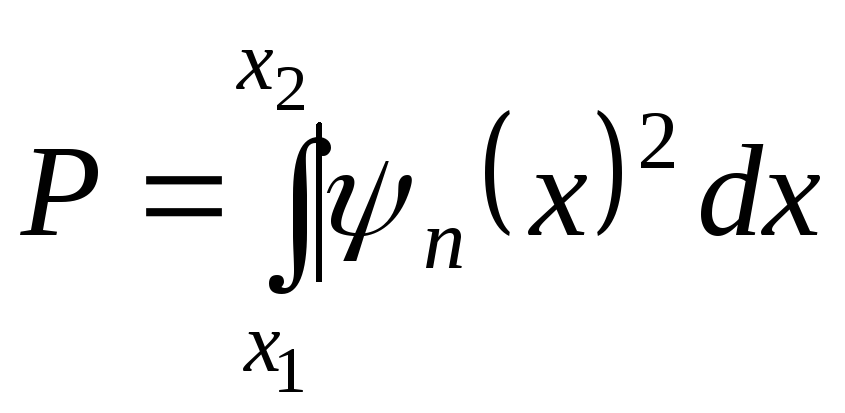, (2.56)

где — нормированная собственная волновая функция, отвечающая данному состоянию.

Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид

. (2.57)

Возбужденному состоянию (п =2) отвечает собственная функция

. (2.58)

Подставив в подинтегральное выражение формулы (2.56) и вынося постоянные величи­ны за знак интеграла, по­лучим

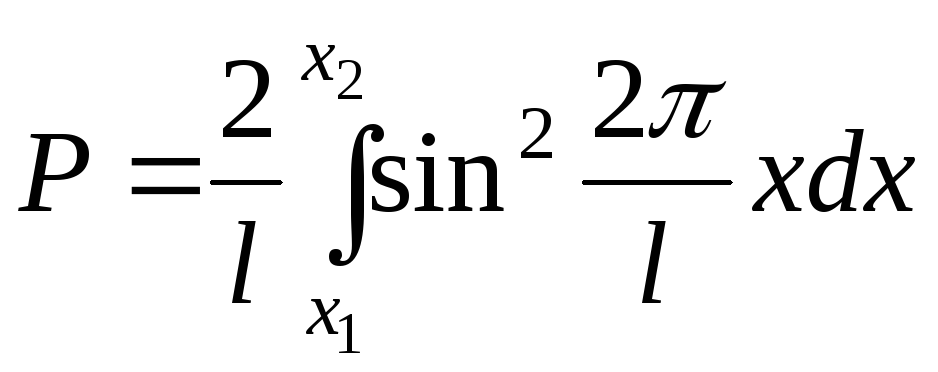. (2.59)

Согласно условию за­дачи, x ₁= и x₂ = (см. рис. 13).

Рис. 13. Бесконечно глубокий потенциальный ящик шириной l (собственная волновая функция соответствует n = 2)

Под­ставим выше указанные пределы интегрирования в формулу (2.59), произведем замену и разобьем инте­грал на два

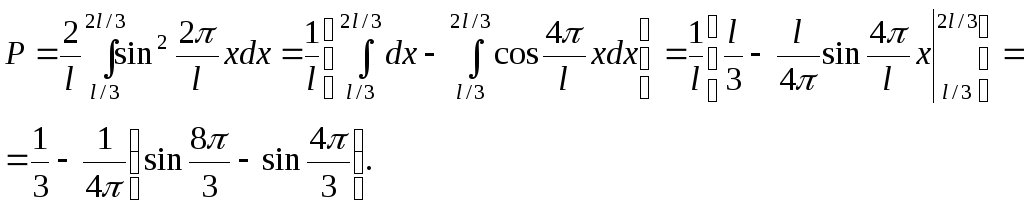
Заметив, что получим Р = 0,195.

ЗАДАЧА №2.40 Две частицы, электрон и протон, обе с энергией 5эВ, движутся в положительном направлении по оси х , встречая на своем пути прямоугольный потенциальный барьер высотой 10эВ и шириной 1пм. Определить отношение вероятностей прохождения частицами этого барьера.

Дано: Е = 5эВ = 5 1,6  10 ^{– 19} Дж = 8 10^{– 19} Дж;

U = 10эВ = 1,6  10 ^{– 18} Дж;

d = 1пм = 10 ^{– 12} м.

Найти : - ?

Решение

Вероятность прохождения частицы сквозь потенциальный барьер определяется коэффициентом прозрачности Р = D.

, (2.60)

где D₀ = 1 (множитель, приравниваемый единице);

m – масса частицы;

= h/2 - постоянная Планка.

Исходя из формулы (2.60) искомое отношение вероятностей прохождения частицами барьера, будет равно

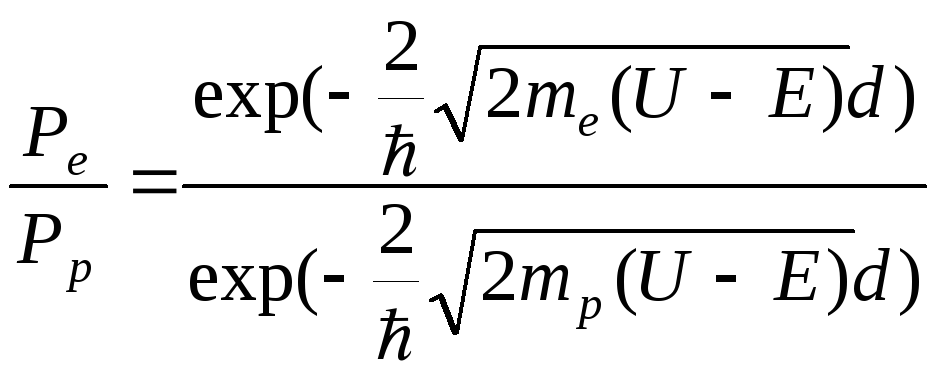, (2.61)

где m_e = 9,1 10 ^{– 31} кг; m_P =1,672 10 ^{– 27} кг; = 1,05 10 ^{– 34} Джс.

Подставляя данные значения, получим

= 2,6.

§2.5 Квантово - механическое описание атома и молекул

ЗАДАЧА №2.41 Какие возможны квантовые состояния электрона в атоме водорода при n = 1 и n = 2, и какие переходы с верхнего уровня на нижний разрешены правилами отбора?

Ответ. Квантовое состояние электрона характеризуется значениями четырех квантовых чисел n, l, m_e, m_s и соответствующей волновой функцией ψ(n, l, m_e, m_s). Система волновых функций и спектральных переходов представлена ниже

n=1 n=2

ψ(2,0,0,1/2)

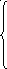ψ(2,0,0,-1/2)

ψ(2,1,0,1/2)

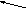ψ(1,0,0,1/2) ψ(2,1,0,-1/2)

ψ(2,1,1,1/2)

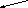ψ(1,0,0,-1/2) ψ(2,1,1,-1/2)

ψ(2,1,-1,1/2)

ψ(2,1,-1,-1/2)

ЗАДАЧА №2.42 Атомный номер натрия Z = 11. Какова электронная конфигурация этого атома в основном состоянии?

Ответ. В основном (невозбужденном) состоянии будут заполняться внутренние слои с наименьшей энергией, а именно: в К-слое – 2 электрона (S); в L-слое – 8 электронов (S и P); в М-слое – один электрон (S).

Электронная конфигурация будет следующей: 1S² 2S² 2P⁶ 3S¹.

ЗАДАЧА №2.43 При каких энергиях возбуждения молекул проявляются чисто вращательные переходы?

Ответ. Для получения вращательных спектров молекул необходима энергия, меньшая энергии колебательных переходов (Е_возб < Е_кол). Эта энергия в области частот радиоволн.

ЗАДАЧА №2.44 Электрон в невозбужденном атоме водорода получил энергию 12,1эВ. На какой энергетический уровень произошел переход? Сколько линий в спектре может проявиться при переходе электрона на более низкие энергетические уровни? Вычислить соответствующие длины волн.

Дано: Е=12,1 эВ;

n₁=1;

R=1,10∙10⁷ м^-1;

с =3∙10⁸ м/с;

h=6,625∙10^-34 Дж∙с.

Найти: n₂ -? N -? λ - ?