Распределение Ферми – Дирака имеет вид

, (1.83)

где - среднее число фермионов в квантовом состоянии с энергиейЕ_i.

Если , то распределения Бозе – Эйнштейна и Ферми – Дирака переходят в классическое распределение Максвелла – Больцмана

, (1.84)

где А – параметр вырождения, он определяется следующим образом

. (1.85)

Система частиц называется вырожденной, если ее свойства, описываемые квантовыми закономерностями, отличаются от свойств обычных систем, подчиняющихся классическим законам. Отступление в поведении бозе – и ферми – газов от классического максвелл-больцмановского газа называется вырождением газов (вырожденный газ). Вырождение газов становится существенным при низких температурах и больших плотностях.

Температурой вырождения Т_В называется температура, при которой вырождение становится существенным. Она определяется из условия

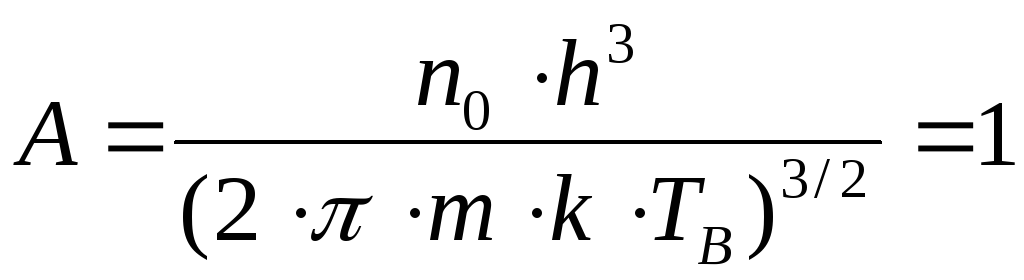, (1.86)

откуда

. (1.87)

Температурный критерий вырождения: Т<<T_B – система частиц вырождена, Т>>Т_В – система частиц не вырождена, и ее поведение описывается классическими законами.

Вырожденный электронный газ в металлах

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми – Дирака

, (1.88)

где - среднее число электронов в квантовом состоянии с энергиейЕ;

- химический потенциал электронного газа при Т=0 К. Кроме того, он является максимальной кинетической энергией, которой обладают электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Ферми и обозначается Е_f (т.е., Е_f =). Поэтому распределение Ферми – Дирака обычно записывается в виде

. (1.89)

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми, которую имеют электроны на этом уровне. Уровень Ферми будет тем выше, чем больше плотность электронного газа.

Молярная теплоемкость электронного газа определяется следующим образом

, (1.90)

где N_A – число Авогадро; k – постоянная Больцмана.

Теория электропроводности металлов, построенная на основе квантовой механики и квантовой статистики Ферми–Дирака, называется квантовой теорией электропроводности металлов. В этой теории с помощью функции распределения Ферми – Дирака выведен закон Ома для плотности тока

j=γE, (1.91)

где γ – удельная электропроводность. Она вычисляется по формуле

γ =, (1.92)

где n₀ – число электронов проводимости в единице объема металла;

u_F – скорость теплового движения такого электрона;

- средняя длина свободного пробега электрона, имеющего энергию Ферми. Она определяется по формуле

, (1.93)

где Е – модуль Юнга; d – период кристаллической решетки; n₀ – число атомов в единице объема; k – постоянная Больцмана; Т - абсолютная температура.

Теплоемкость кристаллов

(классическая теория)

В XIX в. Дюлонг и Пти при измерении теплоемкости твердых тел эмпирически установили закон: теплоемкость одноатомных кристаллов при комнатной температуре очень близка к значению

С_V = 25 Дж/(моль ·К)

и мало изменяется с повышением температуры, стремясь к указанному значению.

Согласно классической модели внутреннего строения твердых тел одноатомный кристалл можно представить как совокупность атомов, колеблющихся в узлах кристаллической решетки под действием упругих сил. Поскольку полная энергия атома в кристалле складывается из кинетической энергии и потенциальной энергии упругих сил, а каждый вид энергии описывается тремя степенями свободы, то общее число степеней свободы равно 6. Колебания каждого атома можно описать тремя степенями свободы. Таким образом, твердое тело в этом случае можно представить как совокупность классических осцилляторов, число которых в одном моле равно числу Авогадро. Применяя для описания поведения такой совокупности осцилляторов классическую теорему о равномерном распределении энергии по степеням свободы, нетрудно найти, что внутренняя энергия моля кристалла будет равна

, (1.94)

а молярная теплоемкость

, (1.95)

что прекрасно согласуется с опытными данными.

Но рассмотренная модель не объясняет температурной зависимости теплоемкости, разницы в поведении диэлектриков и металлов при очень низких температурах, а также исключений из закона Дюлонга и Пти: алмаз, бериллий, бор, кремний и алюминий имеют при комнатной температуре теплоемкость, значительно меньшую 3R. При повышении температуры этих веществ их теплоемкость растет, приближаясь к 3R при существенно более высокой температуре. Строгую теорию теплоемкости можно построить лишь на базе квантовой механики.

Теплоемкость кристаллов по Эйнштейну

Эйнштейн предложил простую модель для объяснения температурного хода теплоемкости кристаллов. Согласно этой модели каждый атом представляет собой осциллятор, колеблющийся с некоторой частотой, одинаковой для всех атомов кристалла. В отличие от классической модели здесь рассматривается квантовый осциллятор, энергия которого может принимать только дискретные значения, кратные , где- частота колебаний осциллятора.

Теплоемкость твердых тел по Эйнштейну будет определена следующим образом

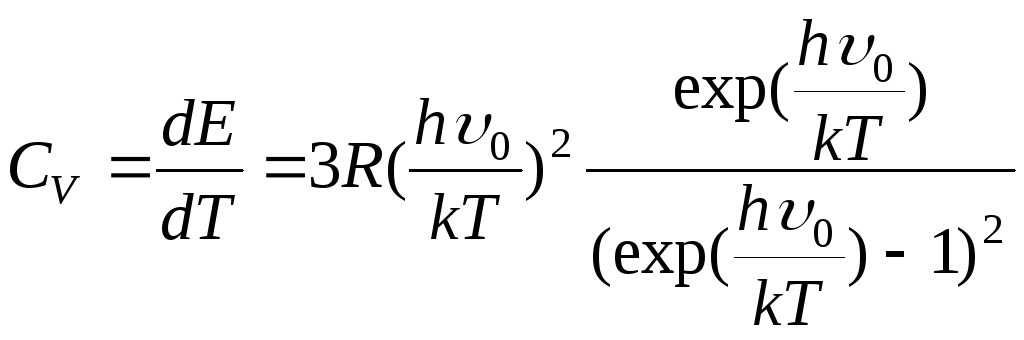. (1.96)

Так как определяется свойствами осцилляторов вещества, то можно ввести характерный параметр

, (1.97)

где -температура Эйнштейна. Вводя в выражение дляС_V, получим

. (1.98)

При теплоемкость стремится к3R.

При очень низких температурах .

Предложенная модель дает качественно верную температурную зависимость теплоемкости диэлектриков, не давая при этом хорошего количественного совпадения с экспериментом, особенно при низких температурах. Следующим шагом в развитии представлений о взаимодействии атомов в кристаллической решетке явилась модель Дебая.