14. Что называется угловой скоростью и угловым ускорением тела? Напишите формулы для их определения.

Угловой скоростью тела называется физическая величина, характеризующая быстроту изменения угла поворота тела во времени, то есть: . Угловая скорость равна первой производной по времени от угла поворота тела.

Угловым ускорением называется такая физическая величина, характеризующая быстроту изменения угловой скорости тела во времени: 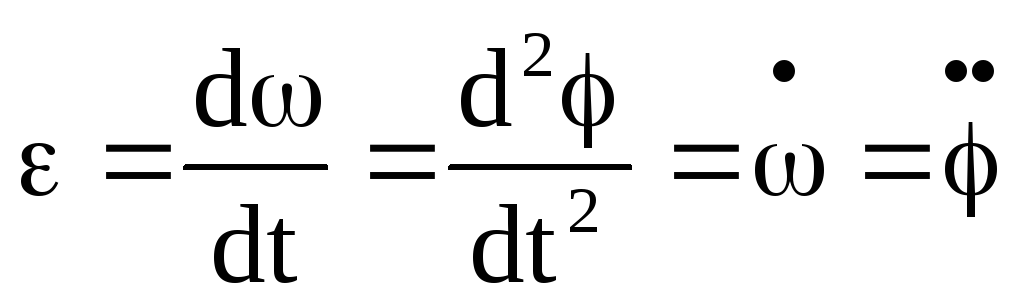. Угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота.

15. Какое вращение твердого тела называется равномерным, какое равномерно-переменным? Запишите уравнения равномерного и равнопеременного вращательного движения.

- Вращение тела называют равномерным, если угловая скорость тела постоянна, то есть угловое ускорение равно нулю: , .

- Равнопеременным вращением называется такое вращательное движение тела, при котором его угловое ускорение постоянно (угловая скорость с каждым одинаковым промежутком времени изменяется да одну и ту же величину): , .

Равномерное: => => . Произвольную константу С определяем из начального условия: . В результате находим: . Тогда: - з-н равномерного вращательного движение твёрдого тела.

Равнопеременное: => => . Произвольную константу С определяем из начального условия: . Тогда: - з-н изменения угловой скорости при равнопеременном вращательном движении твёрдого тела.

Далее: => => . Произвольную константу С определяем из начального условия: . В результате находим: . Окончательно: - з-н равнопеременного вращательного движения твёрдого тела.

16. Какая зависимость существует между угловой скоростью вращающегося тела и числом его оборотов в минуту?

, n – число оборотов в минуту [об/мин], - угловая скорость [].

Пример: n=23 об/мин, найти угловую скорость тела. Решение: .

17. Как изображается угловая скорость тела в виде вектора, как определить направление этого вектора?

В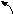ектор угловой скорости тела направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца видел вращение тела против хода часовой стрелки.

18. Как выражается зависимость между угловой скоростью вращающегося тела и линейной скоростью какой-нибудь точки этого тела?

Линейная скорость какой-либо точки вращающегося твёрдого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения.

, то есть: . Модуль , вектора равен: .

19. Напишите формулы для определения касательного и нормального ускорения точки твёрдого тела, вращающегося вокруг неподвижной оси.

Определим тангенциальное и нормальное ускорения точки во вращательном движении вокруг неподвижной оси: , . Модуль полного ускорения точки равен: .

20. Напишите векторные формулы для скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси.

Твёрдое тело вращается вокруг неподвижной оси Оz с угловой скоростью .

- Определим скорость произвольной точки М этого тела:

Угловая

- вектор угловой скорости.

Линейная

Вектор скорости любой точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведённый из произвольного центра, взятого на оси вращения.

- Определим ускорения произвольной точки М этого тела:

Угловое

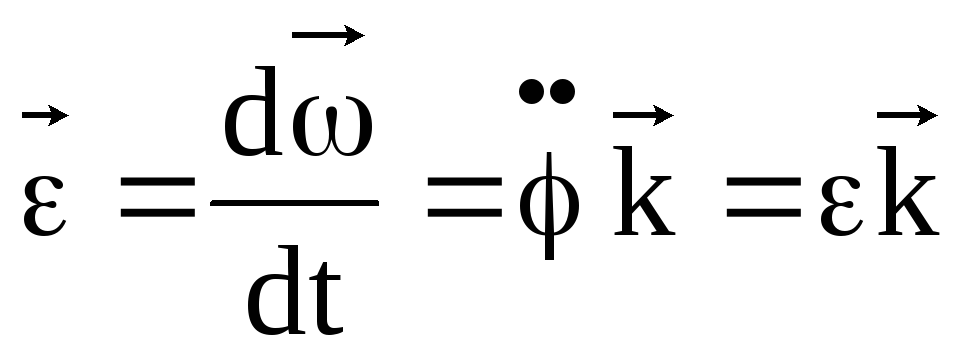- вектор углового ускорения.

Вектор углового ускорения , так же как и вектор угловой скорости , лежит на си вращения. При этом в случае ускоренного вращения вектор направлен в ту же сторону, что и вектор , в случае же замедленного вращения вектор направлен в сторону, противоположную вектору .

Полоное

или

Найдём модули ускорений: