20. Дайте определения пары вращений. Докажите какому движению эквивалентна пара вращений.

Парой вращений (, -) называется совокупность двух вращений твердого тела относительно параллельных осей и с равными по величине, но противоположно направленными угловыми скоростями.

Для произвольной точки М ее абсолютная скорость: , или, учитывая, что

или, учитывая, что =-, имеем: (1)

Векторы и не зависят от положения точки М и поэтому из (1) с учетом произвольности выбора точки М следует, что скорости всех точек тела одинаковы. Таким свойством обладает только поступательное движение. Формулу (1) можно переписать так: (2).

Векторное произведение, стоящее в правой части равенства (2), называется моментом пары вращения который так же, как и момент пары сил, является свободным вектором. Таким образом, пара вращений эквивалентна мгновенно-поступательному движению со скоростью, равной моменту пары угловых скоростей.

20. Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.

Предположим, что тело вращается с угловой скоростью вокруг оси системы координат , которая вращается с угловой скоростью вокруг оси неподвижной системы координат причем оси и параллельны.

Скорость произвольной точки М тела (1). Скорости , и лежат в плоскости, перпендикулярной осям и , а это означает, ввиду произвольности точки М, что тело движется плоскопараллельно.

Найдем в плоскости мгновенный центр вращения. Для точки Р, лежащей на прямой , и коллинеарны и направлены в разные стороны тогда, когда точка Р лежит между и , в случае, если и направлены в одну сторону. Для того, чтобы их геометрическая сумма была равна нулю, нужно чтобы: ·Р=·Р => /Р=/Р

Т.е. точка Р (мгновенный центр скоростей) делит отрезок , внутренним образом на части, обратно пропорциональные модулям угловых скоростей.

В каждом случае скорость точки Р равна нулю: (2).

Вернемся теперь к равенству (1), которое перепишем с учетом того, что:

;

Раскрывая скобки и используя равенство (2), получим:

(3)

С другой стороны, при плоскопараллельном движении: (4), сравнивая (3) и (4), получим:

Таким образом, мы доказали, что совокупность двух вращений твердого тела вокруг параллельных осей, не образующих пару вращений, эквивалентна одному вращению вокруг мгновенной оси с угловой скоростью, равной векторной сумме угловых скоростей составляющих вращений. Мгновенная ось делит расстояние между осями составляющих вращений внутренним образом) на части, обратно пропорциональные модулям угловых скоростей, в зависимости от того, в одну или разные стороны направлены векторы этих скоростей.

20. Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.

П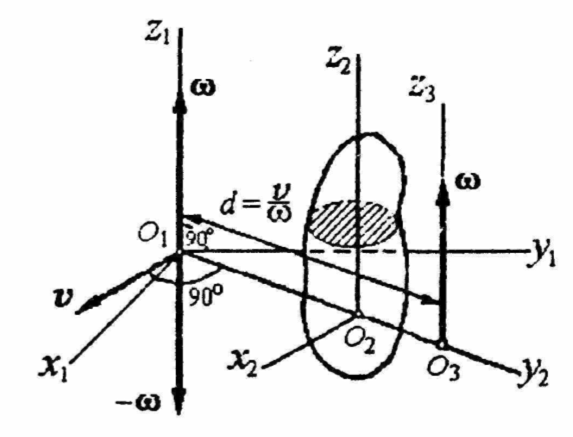усть тело вращается с угловой скоростью вокруг оси жестко скрепленной с другим телом, которое движется поступательно со скоростью . При этом векторы и перпендикулярны.

Так как поступательное движение эквивалентно паре вращений с моментом, равным скорости V, то эту скорость можно заменить парой угловых скоростей (, -), расположенных плоскости, перпендикулярной , причем составляющие пары вращений по модулю равны заданной угловой скорости. Для эквивалентности этой пары вращений данному поступательному движению достаточно следующего условия: .

В этом случае при - плечо пары . В точке векторная сумма и - равна нулю. Следовательно, составное движение тела в случае, когда скорость поступательного движения перпендикулярна угловой скорости вращательного движения, эквивалентно вращению с той же угловой скоростью вокруг мгновенной оси, параллельной оси заданного вращения z и отстоящей от нее на расстоянии .