20. Дайте вывод формулы ускорения Кориолиса и проведите анализ этой формулы.

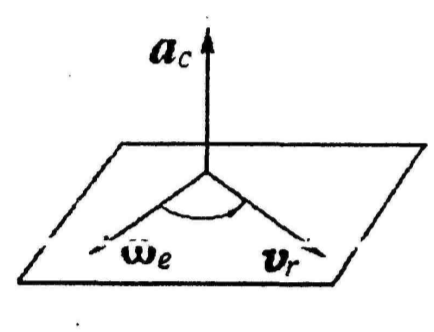
Как видно из приведенной формулы, ускорение Кориолиса равно удвоенному векторному произведению угловой скорости твердого тела, с которым связана подвижная система отсчета, на скорость точки относительно этой подвижной системы. Направлен вектор так же, как и вектор , т.е. перпендикулярно плоскости, проходящей через векторы и в ту сторону, откуда кратчайшее совмещение с видно происходящим против хода часовой стрелки.

как видно из векторной формулы, модуль ускорения Кориолиса определяется следующим образом: .

Ускорение Кориолиса равно нулю, когда:

- , т.е. когда переносное движение поступательное или если переносная угловая скорость в данный момент времени обращается в нуль;

- , т.е. в данный момент относительная скорость обращается в нуль;

- , т.е. векторы и коллинеарны.

Д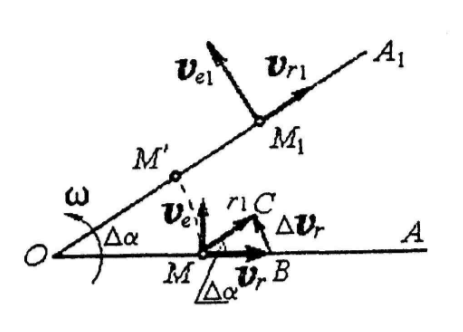опустим, что прямая ОА вращается вокруг точки О с постоянной угловой скоростью , а вдоль этой прямой движется точка М с постоянной относительной скоростью . Пусть положение ОА рассматриваемой прямой соответствует моменту времени t. В этот момент точка занимает положение М, ее переносная скорость по величине равна ·ОМ и направлена перпендикулярно прямой ОА. За промежуток времени t прямая ОА повернется на угол α и займет положение . Точка на прямой к этому моменту времени займет положение , т. е. пройдет путь, равный отрезку М. Переносная скорость точки в момент t +t по величине равна ·О и направлена перпендикулярно прямой . Мы видим, что переносная скорость точки М изменяется не только по величине, но и по направлению, и это изменение происходит как следствие относительного движения точки, т.е. перемещения её по прямой на расстояние М.

Изменение переносной скорости по величине за промежуток времени t равно:

Отношение этого изменения переносной скорости к промежутку времени t в пределе при t0 дает добавочную величину ускорения, вызванного относительным движением. Назовем эту величину . Тогда:

Направление вектора , модуль которого равен , в пределе при t0 совпадает с направлением вектора переносной скорости, т.е. перпендикулярно ОА.

Рассмотрим теперь изменение относительной скорости. В нашем примере величина относительной скорости постоянна, однако в связи с движением прямой ОА относительная скорость изменяется по направлению. Найдем ту добавочную величину ускорения, которая необходима для изменения относительной скорости по направлению. Обозначим эту искомую величину через .

Тогда , где векторы и равны по модулю, но различны по направлению, и угол между ними равен α.

Определим модуль и направление вектора . Из равнобедренного треугольника ОВС следует:

, тогда:

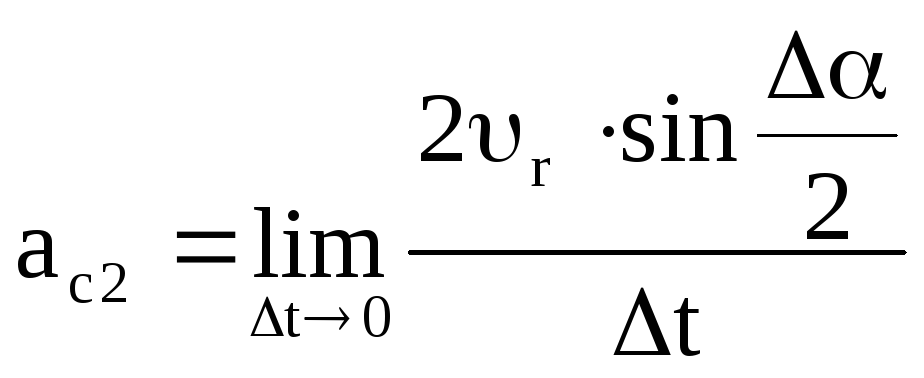
Умножая числитель и знаменатель последней формулы на α после некоторых очевидных преобразований получим

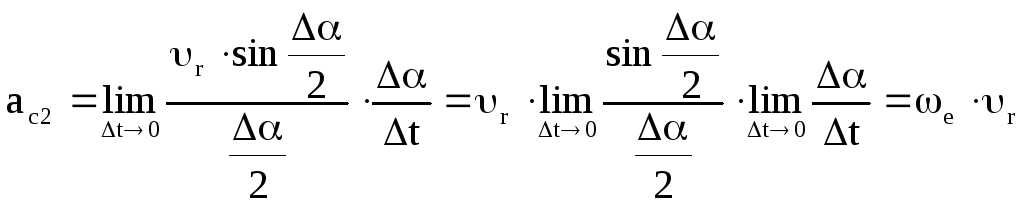
Направление совпадает с предельным направлением вектора и при α0 перпендикулярно прямой ОА, т.е. .

Значит, оба вектора и совпадают и по величине и по направлению. Их сумма составляет величину Кориолиса: .