
- •Связь между координатным и векторным способом:
- •Докажите формулу распределения скоростей точек плоской фигуры.
- •Сформулируйте и докажите теорему о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки.
- •Опишите, как определяется скорость точек плоской фигуры и её угловая скорость с помощью мгновенного центра скоростей.
- •Опишите частные случаи определения положения мгновенного центра скоростей.
- •Докажите формулу распределения ускорений точек плоской фигуры.
- •Дайте определения мгновенного центра ускорений. Как определить его положение? Как определяются ускорения точек плоской фигуры с помощью мгновенного центра скоростей.
- •Докажите формулу для определения скоростей точек тела, движущегося около неподвижной точки.
- •Доказать формулу распределения ускорений точек твердого тела, движущегося около неподвижной точки. Формулы вращательного и осестремительного ускорений и их направления.
- •Дайте определения сложного движения точки и основных понятий этого движения.
- •Сформулируйте и докажите теорему о сложении скоростей в сложном движении точки.
- •Сформулируйте и докажите теорему о сложении ускорений в сложном движении точки.
- •Дайте вывод формулы ускорения Кориолиса и проведите анализ этой формулы.
- •Дайте определения пары вращений. Докажите какому движению эквивалентна пара вращений.
- •Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.
- •Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.
-
Доказать формулу распределения ускорений точек твердого тела, движущегося около неподвижной точки. Формулы вращательного и осестремительного ускорений и их направления.
Д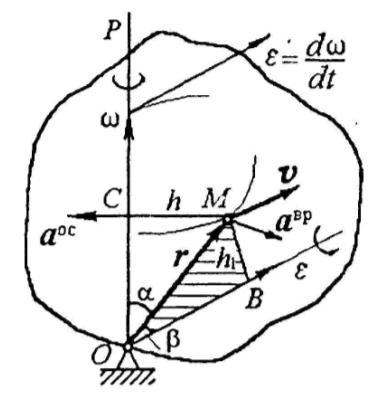 ля
определения ускорения точки М твердого
тела, движущегося около неподвижной
точки О, дифференцируем по времени обе
части формулы
ля
определения ускорения точки М твердого
тела, движущегося около неподвижной
точки О, дифференцируем по времени обе
части формулы
![]() .
В результате получим:
.
В результате получим:
![]() (1)
(1)
Учитывая, что:
![]() и
и
![]() ,
запишем формулу (1) так:
,
запишем формулу (1) так:
![]() (2).
(2).
Таким образом, ускорение точки М в данный
момент слагается из двух составляющих.
Первое слагаемое называется вращательным
ускорением:
![]() .
.
Вектор вращательного ускорения
![]() перпендикулярен плоскости, проходящей
через вектор углового ускорения и
радиус-вектор точки М. Здесь следует
напомнить, что вектор
перпендикулярен плоскости, проходящей
через вектор углового ускорения и
радиус-вектор точки М. Здесь следует
напомнить, что вектор
![]() не лежит на той же прямой, что и вектор
не лежит на той же прямой, что и вектор
![]() .
Поэтому вектор
.
Поэтому вектор
![]() перпендикулярен не радиусу вращения
h, а отрезку
перпендикулярен не радиусу вращения
h, а отрезку
![]() ,
который равен кратчайшему расстоянию
от точки М до оси вектора углового
ускорения. Модуль вращательного
ускорения:
,
который равен кратчайшему расстоянию
от точки М до оси вектора углового
ускорения. Модуль вращательного
ускорения:
![]()
Второе слагаемое в формуле (2) называется
осестремительным ускорением:
![]()
Оно направлено перпендикулярно плоскости
![]() и
и
![]() ,
т.е. по кратчайшему расстоянию от точки
М до мгновенной оси вращения, причем
всегда в ту сторону, откуда поворот от
,
т.е. по кратчайшему расстоянию от точки
М до мгновенной оси вращения, причем
всегда в ту сторону, откуда поворот от
![]() к
к
![]() на наименьший угол происходит против
хода часовой стрелки. Модуль
осестремительного ускорения:
на наименьший угол происходит против
хода часовой стрелки. Модуль
осестремительного ускорения:
![]() .
.
Таким образом, формула (2) выражает следующую теорему. Ускорение точек твердого тела, движущегося вокруг неподвижной точки, равно геометрической сумме вращательного и осестремительного ускорений.
-
Дайте определения сложного движения точки и основных понятий этого движения.
- Движение, совершаемое точкой М
относительно неподвижной системы
координат
![]() ,
называется абсолютным. Траектория этого
движения называется абсолютной
траекторией, скорость - абсолютной
скоростью и ускорение - абсолютным
ускорением. Абсолютные скорость и
ускорение обозначаются
,
называется абсолютным. Траектория этого
движения называется абсолютной
траекторией, скорость - абсолютной
скоростью и ускорение - абсолютным
ускорением. Абсолютные скорость и
ускорение обозначаются
![]() ,
и
,
и
![]() .
.
- Другую систему, Oxyz, которая движется
относительно системы
![]() ,
назовем относительной.
,
назовем относительной.
Движение точки М относительно подвижной системы координат Oxyz называется относительным движением. Такое движение будет видеть наблюдатель, связанный с подвижными осями и перемещающийся вместе с ними. Траектория точки, описываемая в относительном движении, называется относительной траекторией. Понятно, что относительная траектория точки не остается неподвижной, а перемещается в пространстве вместе с подвижной системой координат.
Скорость точки М относительно подвижной
системы координат называется относительной
скоростью, а ускорение - относительным
ускорением. Относительные скорости и
ускорения обозначаются так:
![]() и
и
![]() .
Из определения относительного движения
следует, что при вычислении
.
Из определения относительного движения
следует, что при вычислении
![]() и
и
![]() необходимо мысленно движение осей Oxyz
остановить, т.е. рассматривать оси Oxyz
как неподвижные и воспользоваться
правилами и формулами кинематики точки.
необходимо мысленно движение осей Oxyz
остановить, т.е. рассматривать оси Oxyz
как неподвижные и воспользоваться
правилами и формулами кинематики точки.
- Движение, совершаемое подвижной
системой координат Oxyz вместе с неизменно
связанным с ней пространством и движущейся
в нем точкой относительно неподвижной
системы
![]() называется переносным движением.
называется переносным движением.
Скорость той точки М1 пространства,
связанного с подвижной системой
координат, с которой в данный момент
совпадает рассматриваемая точка М,
называется переносной скоростью, а
ускорение - переносным ускорением.
Переносные скорость и ускорение
обозначают соответственно
![]() и
и
![]() .
.
