20. Дайте определения мгновенного центра ускорений. Как определить его положение? Как определяются ускорения точек плоской фигуры с помощью мгновенного центра скоростей.

П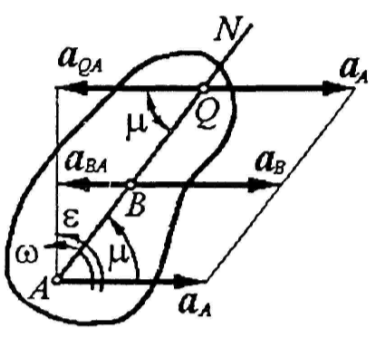ри непоступательном движении плоской фигуры в её плоскости, на фигуре (или на вязанной с ней подвижной плоскостью) в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений.

Если известно ускорение какой-либо точки А плоской фигуры, а также её угловая скорость и угловое ускорение. Тогда положение мгновенного центра ускорений определяется следующим образом:

1. Находим значение угла из формулы: .

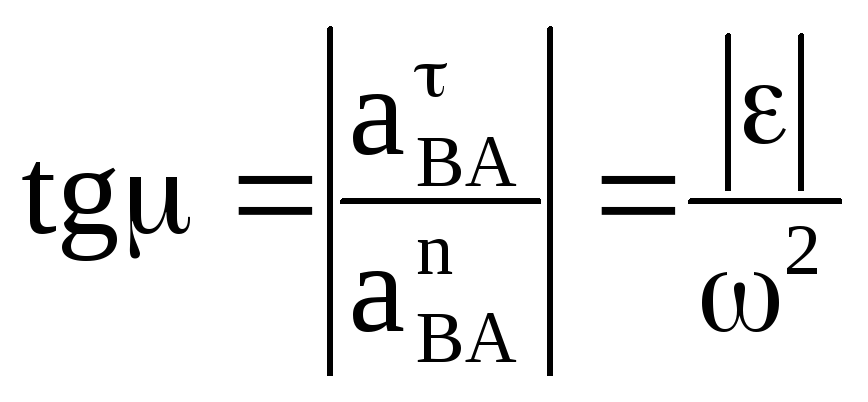2. Из точки А, ускорение которой известно, под углом к вектору проводим полупрямую AN, которая должна быть отклонена от на угол в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, то есть в строну направления углового ускорения , показанного на рисунку дуговой стрелкой.

3. На полученной полупрямой AN отложим отрезок . Конец Q этого отрезка и будет мгновенным центром ускорений.

Если точку Q выбрать за полюс, то, поскольку , ускорение любой точки М плоской фигуры, согласно формуле , будет равно ускорению точки М во вращательном движении этой точки вокруг мгновенного центра ускорений, то есть: . Модуль ускорения точки М будет равен . Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение было вращательным вокруг мгновенного центра ускорений. При этом выполняются следующие условия: .

20. Докажите формулу для определения скоростей точек тела, движущегося около неподвижной точки.

Пусть твердое тело имеет одну неподвижную точку О. Свяжем с телом систему координат Oxyz. Эта система однозначно определяет положение рассматриваемого тела относительно неподвижной системы координат . Положение произвольной точки М тела определяется радиус-вектором . Если x,y,z - координаты точки М в подвижной системе координат, а - единичные векторы этой системы, то радиус-вектор может быть представлен так: (1).

В формуле (1) координаты х, у, и z постоянны, а векторы являются функциями времени, так как система координат Oxyz движется вместе с телом. Учитывая, что: продифференцируем по времени формулу (1), тогда: (2).

Найдем теперь проекции скорости точки М на оси х, у и z, для чего умножим обе части равенства (2) скалярно на :

, , (3)

Так как векторы взаимно перпендикулярны, между ними существует следующие шесть зависимостей: , , , , , .

Дифференцируя эти равенства по времени, найдем две группы формул:

, , , , (4)

В результате формулы (3) с учетом (4) можно записать так:

, , (5)

Если обозначить: , , (6) и ввести в рассмотрение такой вектор:

, то равенства (5) с учетом (6) можно переписать так:

, , (7)

Рассмотрим теперь такое векторное произведение:

П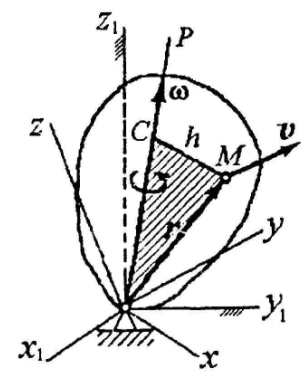роекции этого векторного произведения равны, согласно формулам (7), проекциям вектора скорости, следовательно: (8). Введенный нами вектор направлен вдоль прямой, проходящей через начало координат, в каждой точке которой скорости точек тела в данный момент равны нулю, т.е. вдоль мгновенной оси вращения. Это следует из того, что геометрическое место точек, скорость которых равна нулю, определяется уравнением , что является условием коллинеарности этих векторов.

Таким образом, скорости точек тела, имеющего одну неподвижную точку, распределяются так, как если бы тело вращалось вокруг неподвижной оси, совпадающей в данный момент с мгновенной осью вращения. Назовем вектор вектором мгновенной угловой скорости. Модуль скорости точки М определяется равенством

где h - кратчайшее расстояние от точки М до мгновенной оси вращения. Вектор перпендикулярен плоскости, проходящей через точку М и мгновенную ось ОР в сторону поворота тела.