
- •Связь между координатным и векторным способом:
- •Докажите формулу распределения скоростей точек плоской фигуры.
- •Сформулируйте и докажите теорему о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки.
- •Опишите, как определяется скорость точек плоской фигуры и её угловая скорость с помощью мгновенного центра скоростей.
- •Опишите частные случаи определения положения мгновенного центра скоростей.
- •Докажите формулу распределения ускорений точек плоской фигуры.
- •Дайте определения мгновенного центра ускорений. Как определить его положение? Как определяются ускорения точек плоской фигуры с помощью мгновенного центра скоростей.
- •Докажите формулу для определения скоростей точек тела, движущегося около неподвижной точки.
- •Доказать формулу распределения ускорений точек твердого тела, движущегося около неподвижной точки. Формулы вращательного и осестремительного ускорений и их направления.
- •Дайте определения сложного движения точки и основных понятий этого движения.
- •Сформулируйте и докажите теорему о сложении скоростей в сложном движении точки.
- •Сформулируйте и докажите теорему о сложении ускорений в сложном движении точки.
- •Дайте вывод формулы ускорения Кориолиса и проведите анализ этой формулы.
- •Дайте определения пары вращений. Докажите какому движению эквивалентна пара вращений.
- •Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.
- •Сложение вращений твёрдого тела относительно параллельных осей. Рассмотреть случай, когда угловые скорости направлены в одну сторону.
-
Опишите частные случаи определения положения мгновенного центра скоростей.
П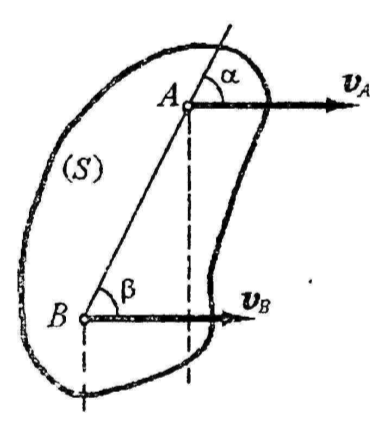 усть
скорости
усть
скорости
![]() и
и
![]() любых двух точек А и В параллельны друг
другу и при этом линия АВ не перпендикулярна
к
любых двух точек А и В параллельны друг
другу и при этом линия АВ не перпендикулярна
к
![]() ,
а следовательно, и к
,
а следовательно, и к
![]() .
Из теоремы о проекциях скоростей двух
точек на прямую, соединяющую эти точки,
следует, что:
.
Из теоремы о проекциях скоростей двух
точек на прямую, соединяющую эти точки,
следует, что:
![]() ,
но
,
но
![]() ,
поэтому
,
поэтому
![]() =
=![]() и, следовательно,
и, следовательно,
![]() =
=![]() .
Таким образом, в рассматриваемом случае
скорости всех точек плоской фигуры в
данный момент равны и по модулю, и по
направлению. Такое состояние плоской
фигуры называется мгновенно поступательным.
Так как перпендикуляры, восстановленные
из точек А и В к скоростям этих точек,
не пересекаются, то в рассматриваемом
случае в данный момент мгновенный центр
скоростей находится в бесконечности.
Угловая скорость
.
Таким образом, в рассматриваемом случае
скорости всех точек плоской фигуры в
данный момент равны и по модулю, и по
направлению. Такое состояние плоской
фигуры называется мгновенно поступательным.
Так как перпендикуляры, восстановленные
из точек А и В к скоростям этих точек,
не пересекаются, то в рассматриваемом
случае в данный момент мгновенный центр
скоростей находится в бесконечности.
Угловая скорость
![]() плоской фигуры в этот момент равна нулю.
плоской фигуры в этот момент равна нулю.
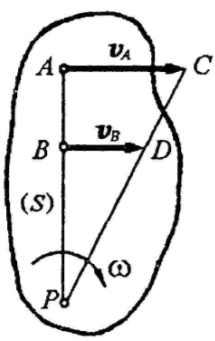
Пусть скорости
![]() и
и
![]() точек А и В параллельны друг другу и эти
точки лежат на одном перпендикуляре к
данным скоростям. В этом случае при
точек А и В параллельны друг другу и эти
точки лежат на одном перпендикуляре к
данным скоростям. В этом случае при
![]() мгновенный центр скоростей Р определяется
построениями.
мгновенный центр скоростей Р определяется
построениями.
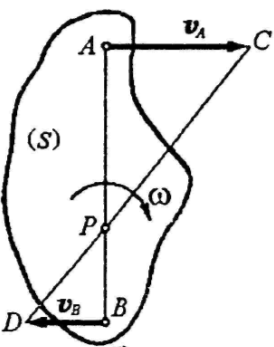
В этом случае для нахождения мгновенного
центра скоростей Р нужно, кроме
направлений, знать еще и модули скоростей
![]() и
и
![]() .
.
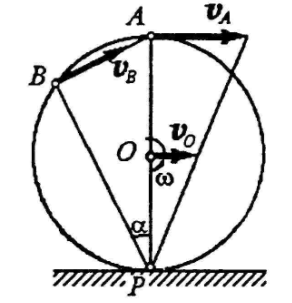
В практических задачах часто приходится
иметь дело со случаем, когда плоская
фигура катится без скольжения по
некоторой неподвижной кривой MN.
практических задачах часто приходится
иметь дело со случаем, когда плоская
фигура катится без скольжения по
некоторой неподвижной кривой MN.
В этом случае скорость точки касания контура плоской фигуры с кривой MN равна нулю, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковые скорости, а кривая MN неподвижна. Отсюда следует, что точка касания Р является мгновенным центром скоростей плоской фигуры.
-
Докажите формулу распределения ускорений точек плоской фигуры.
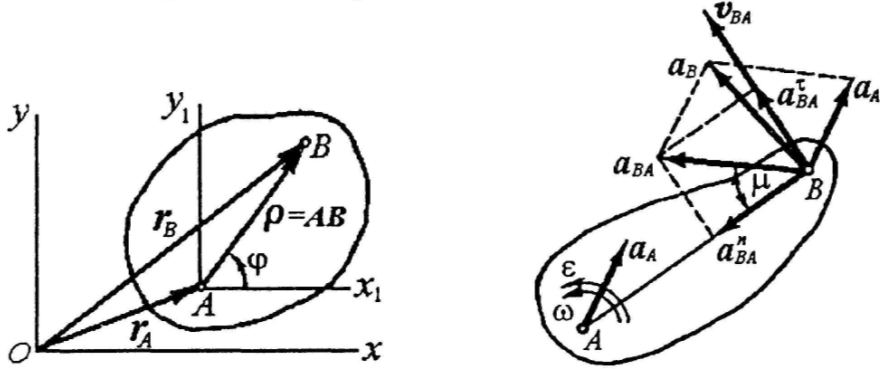
Пусть плоская фигура (S) движется
относительно неподвижной системы
координат Оху. В этой системе положения
полюса А и произвольной точки В
определяются соответственно
радиус-векторами
![]() и
и
![]() .
.
Скорость произвольной точки В можно определить с помощью формулы распределения скоростей
![]() (1), где
(1), где
![]() радиус-вектор, проведенный из полюса А
в точку В. Дифференцируя равенство (1)
по времени, получим:
радиус-вектор, проведенный из полюса А
в точку В. Дифференцируя равенство (1)
по времени, получим:
![]() (1).
(1).
Здесь
![]() ,
,
![]() ,
т.е. соответственно равны ускорениям
полюса А и точки В. Производная
,
т.е. соответственно равны ускорениям
полюса А и точки В. Производная
![]() есть вектор углового ускорения фигуры,
направленный (как и
есть вектор углового ускорения фигуры,
направленный (как и
![]() )
перпендикулярно к плоскости фигуры.
Кроме того, согласно формуле
дифференцирования вектора, постоянного
по модулю:
)
перпендикулярно к плоскости фигуры.
Кроме того, согласно формуле
дифференцирования вектора, постоянного
по модулю:
![]() ,
тогда:
,
тогда:
![]()
Учитывая, что
![]() и
и
![]() ,
получим:
,
получим:
![]() .
.
В результате равенство (1) окончательно
можно записать так:
![]() .
.
Введём обозначения:
![]() и
и
![]() (2).
(2).
Векторы
![]() и
и
![]() представляют те касательное и нормальное
ускорения, которые имела бы точка В,
если бы фигура (S) совершала только
вращение вокруг полюса А. Пользуясь
правилом составления векторного
произведения, легко убедиться, что
представляют те касательное и нормальное
ускорения, которые имела бы точка В,
если бы фигура (S) совершала только
вращение вокруг полюса А. Пользуясь
правилом составления векторного
произведения, легко убедиться, что
![]() имеет направление, совпадающее с вектором
имеет направление, совпадающее с вектором
![]() (от точки к полюсу), а
(от точки к полюсу), а
![]() = перпендикулярно
= перпендикулярно
![]() .
.
Модули этих векторов определяются так:
![]() ,
,
![]() .
.
Используя обозначения (2), окончательно находим формулу распределения ускорений:
![]() ,
или
,
или
![]() ,
где
,
где
![]() .
.
Таким образом, ускорение любой точки В плоской фигуры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в её вращательном движении вместе с плоской фигурой вокруг этого полюса.
