20. Докажите формулу распределения скоростей точек плоской фигуры.

Пусть плоская фигура движется относительно неподвижной системы координат Оху. В этой системе положения полюса А и произвольной точки В определяются соответственно радиус-векторами и . Между этими векторами и и вектором в любой момент времени имеет место следующее соотношение: (1).

Вектор определяет положением произвольной точки В относительно системы , перемещающейся вместе с полюсом А поступательно. Подчеркнем еще раз, что движение сечения по отношению к осям представляет собой вращение вокруг полюса А.

Дифференцируя обе части равенства (1) по времени, получим: (2).

В полученном равенстве (2) , . Что же касается , то это - скорость, которую точка В получает при вращении вокруг полюса А. Обозначим эту скорость через .

Вектор есть постоянный по модулю вектор, изменяющийся при движении фигуры только по направлению. Для него справедлива формула: . Тогда формула распределения скоростей примет вид: или .

Следовательно, скорость любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости другой, произвольно выбранной и принятой за плюс, точки А и скорости точки В в ее вращении вместе с плоской фигурой вокруг этого полюса. Вектор направлен перпендикулярно АВ в сторону вращения фигуры, а по модулю эта скорость определяется так: .

Таким образом, определив вращательную скорость точки В вокруг полюса А и зная скорость этого полюса, мы можем найти искомую скорость точки В как диагональ параллелограмма, построенного на скоростях и .

20. Сформулируйте и докажите теорему о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки.

Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.

Рассмотрим какие-нибудь две точки А и В, движущиеся в своей плоскости плоской фигуры (S). Предположим, что известны модуль и направление скорости точки А и направление скорости точки В. Принимая точку А за полюс, можно записать, что: .

Проецируя обе части этого равенства на линию АВ и учитывая, что вектор перпендикулярен к АВ, приходим к результату

Доказанная теорема позволяет находить модуль скорости точки В, если известны модуль и направление скорости точки А и направление скорости точки В.

20. Опишите, как определяется скорость точек плоской фигуры и её угловая скорость с помощью мгновенного центра скоростей.

П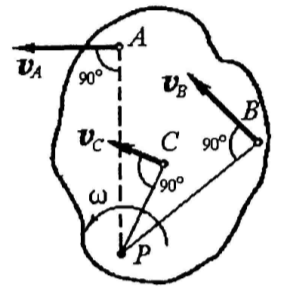редположим теперь, что мгновенный центр скоростей Р известен. Найдем с помощью формулы распределения скоростей величины скоростей двух любых точек, например А и В. При этом следует помнить, что скорость полюса (т.е. мгновенного центра скоростей) равна нулю. В этом случае: , (1).

Векторы и перпендикулярны отрезкам АР и ВР соответственно и направлены в сторону вращения плоской фигуры. Назовем отрезок, соединяющий мгновенный центр скоростей с данной точкой, мгновенным радиусом вращения. Таким образом, мы видим, что поле скоростей точек плоской фигуры в каждый момент таково, как будто фигура вращается вокруг неподвижного мгновенного центра. При этом скорости точек плоской фигуры перпендикулярны мгновенным радиусам вращения и по величине пропорциональны расстояниям этих точек до мгновенного центра скоростей. Из равенств (1) следует: (2), т.е. модуль угловой скорости плоской фигуры в каждый момент равен отношению величины скорости какой-либо точки плоской фигуры к расстоянию от этой точки до мгновенного центра скоростей. Кроме того, так как , а из формулы распределения скоростей следует, что , тo тогда (3).

Эти результаты приводят к следующим выводам:

1. Для определения положения мгновенного центра скоростей надо знать только направление скоростей и каких-нибудь двух точек А и В сечения (S). Мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных из точек А и В к скоростям этих точек.

2. Для определения скорости любой точки тела достаточно знать модуль и направление какой-нибудь одной точки А тела и направление скорости другой его точки В. Тогда, восстановив из точек А и В перпендикуляры к направлениям их скоростей и , найдем положение мгновенного центра скоростей Р и по направлению скорости определим направление вращения тела. После этого, зная модуль скорости , найдем по формуле (2) скорость любой точки.

3. Модуль угловой скорости тела, как видно из формулы (2), в каждый данный момент равен отношению модуля скорости какой-нибудь точки сечения (S) к расстоянию от этой точки до мгновенного центра скоростей Р. Кроме того, модуль угловой скорости тела можно определить с помощью формулы (3).