28

1. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

Движение точки в пространстве определяется тремя ос­новными способами: векторным, координатным и естествен­ным. Векторный способ задания движения применяется при тео­ретических исследованиях, координатный и естественный упот­ребляются преимущественно при решении задач.

Векторный способ задания движения точки

Выберем некоторый неподвижный центр О и проведем из этого центра в точку М, движение которой изучаем, радиус-вектор r (рис. 2.1). При движении точки М радиус-вектор r изме­няется по величине и по направлению. Каждому моменту време­ни t соответствует определенное значение r.

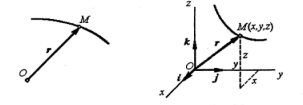
Рис. 2.1 Рис. 2.2

Следовательно, радиус-вектор r однозначно определяет положение точки М. Таким образом, чтобы определить движение точки, нужно задать ее радиус-вектор в виде однозначной и не­прерывной функции времени:

r = r(t) (1)

Уравнение (1) определяет положение точки М в про­странстве в произвольный момент времени t, следовательно, уравнение (1) определяет закон движения точки М. При вектор­ном способе задании движения траекторией точки будет годо­граф радиус-вектора r.

Координатный способ задания движения точки

Рассмотрим прямоугольную декартову систему коорди­нат. Положение движущейся точки М определяется координата­ми х, у, z (рис. 2.2). Если координаты точки заданы как однознач­ные функции времени

x = x(t), y=y(t), z = z(t), (2)

то положение точки М в пространстве известно в каждый момент времени. Уравнения (2) определяют закон движения точки и на­зываются уравнениями ее движения. С математической точки зрения уравнения (2) представляют собой параметрические урав­нения траектории точки. Чтобы найти уравнение траектории в форме зависимостей между координатами точки М, нужно из уравнений (2) исключить время, т.е. параметр t. Решая, например, последнее уравнение из (2) относительно t, найдем t = φ (z). Подставляя это соотношение в первые два уравнения, получим:

x = x(φ(z)), y=y(φ(z)),

Плоскость:

x = x(t), y=y(t)

Прямая:

x = x(t)

Вышесказанное применимо для декартовой системы координат, для полярной:

ρ =ρ(t) φ=φ(t),

где ρ – полярный радиус, φ – угол между полярной осью и полярным радиусом

Связь между координатным и векторным способом:

r = x(t)i + y(t)j + z(t)k (7)

Равенство (7) устанавливает зависимость радиус-вектора точки М от времени и решает вопрос о переходе от координатно­го способа задания движения точки к векторному.

Естественный способ задания

Этот способ задания движения точки применяется в том случае, когда траектория точки, относительно выбранной систе­мы отсчета, известна. Выберем на этой траектории какую-нибудь неподвижную точку А и примем ее за начало отсчета (рис. 2.3).

Далее, рассматривая траекторию как криволинейную координатную ось, сообщим ей ориентацию, т.е. поло­жительное направление отсчета рас­стояний s - AM. Тогда положение точки М на траектории будет одно­значно определяться криволинейной координатной s, равной расстоянию от точки А до движущейся точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точки М криво­линейная координатам будет изменяться с течением времени, т. е. 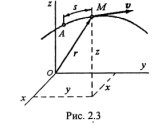s = s(t)

Зная уравнение (8), можно определить положение точки в каж­дый момент времени. Уравнение (8) называется уравнением дви­жения, или законом движения вдоль заданной траектории.

Рассмотрим связь между естественным и координатным способами задания движения точки. Для перехода от координат­ного способа задания движения к естественному необходимо:

1) определить уравнение траектории точки,

2) положение точки в начальный момент времени и

3) закон движения точки по ее траектории.

Как определить уравнение траектории, нам уже известно. Для определения положения движущейся точки в начальный мо­мент времени (/ = 0) необходимо в уравнения (2) подставить t = 0. Для определения закона движения точки по траектории восполь­зуемся известкой из математического анализа формулой длины дуги кривой

В теоретической механике дифференцирование по вре­мени принято обозначать точкой над дифференцируемой функ­цией. Перепишем формулу (9) в этих обозначениях.

Знак плюс в формулах (9), (10) берется в том случае, ко­гда точка М движется в сторону с положительного отсчета кри­волинейной координаты s. Если направление движения точки по траектории изменяется, то знак корня может быть различным для различных интервалов времени. Это изменение знака может быть при колебательном движении точки.

2. СКОРОСТЬ ТОЧКИ ПРИ ВЕКТОРНОМ СПОСОБЕ ЗАДАНИЯ ЕЁ ДВИЖЕНИЯ

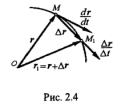
Пусть в некоторый момент времени t положение точки М определяется радиус-вектором r(t), а в момент t₁=t+∆t - радиус-вектором r₁= r+∆r (рис. 2.4). Тогда перемещение точки М за промежуток времени ∆t=t₁-t будет ММ₁ = r₁-r = ∆r.

Будем считать, что промежуток времени ∆t настолько мал, что с достаточной степенью точно­сти можно предполагать перемещение точки М в положение М₁, происходящим равномерно и прямолинейно. В этом слу­чае скорость точки М можно приближен­но вычислить так:

(1)

Для того, чтобы точно вычислить скорость точки в данный мо­мент времени, необходимо в формуле (1) перейти к пределу при стремлении промежутка времени ∆t к нулю, т.е.

Этот предел представляет собой первую векторную про­изводную по времени от радиус-вектора точки по времени. Сле­довательно, скорость точки в данный момент времени есть век­торная величина, равная первой производной от радиус-вектора точки по времени

3. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ

Рассмотрим движение точки относительно прямоуголь­ной системы координат (рис. 2.5). В этом случае координаты точ­ки заданы как функции времени:

x = x(t), y = y(t), z = z(t). (1)

Разложим радиус-вектор г по ортам декартовой системы координат:

r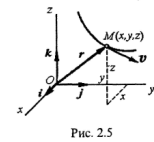 = x(t)i + y(t)j +z(t)k. (2)

Зная, что вектор скорости равен пер­вой производной от радиус-вектора, продифференцируем равенство (2) по времени. В результате получим разло­жение скорости по ортам i, j, к:

(3)

С другой стороны разложение по ортам вектора скорости V по ортам i, j, к можно представить как:

(4)

Сравнивая формулы (3) и (4):

(5)

Таким образом, проекции скорости на неподвижные де­картовы оси координат равны первым производным по времени от соответствующих координат движущейся точки.

Из равенства (5) следует, что проекции скорости точки на координатные оси равны скорости проекции этой точки на те же оси. Зная проекции вектора скорости точки V, найдем его модуль:

или (6)

Направляющие косинусы:

4. СКОРОСТЬ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ

Движение точки задано естественным способом. Известны траектория и закон s=s(t) (рис. 2.6). Каждой точке траектории соответствует определенный радиус-вектор r(t). Так как положение каждой точки траектории определяется дуговой координатой s, то радиус-вектор r можно рассматривать как сложную функцию времени t. Тогда:

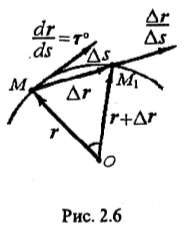(1)

Теперь найдем вектор скорости V:

(2)

Известно, что . Далее, так как направление ∆r=MM₁ в пределе (при ∆S → 0) совпадает с касательной к траектории в точке M, то вектор есть единичный вектор касательной к траектории (ее орт), направлен­ный в сторону возрастания криволинейной координаты S. Обо­значая орт касательной τ°, запишем формулу (2) в виде

(3)

Учитывая, что , а τ°∙τ° = 1, получим т.е. проекция вектора скорости точки на направление касатель­ной к траектории равна первой производной по времени от кри­волинейной координаты S no времени. Тогда формулу (3) можно записать так:

Из формулы (5) следует, что модуль скорости . Если > 0, то точка движется в положительном направлении отсчета расстояний и . Если же < 0, точка движется в от­рицательном направлении . Таким образом, модуль век­тора скорости точки равен модулю ее проекции на направление касательной:

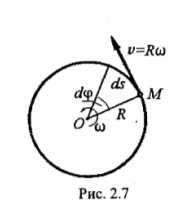
При движении по окружности:

5. УСКОРЕНИЕ ТОЧКИ ПРИ ВЕКТОРНОМ СПОСОБЕ ЗАДАНИЯ

Ускорение - физическая величина, характеризующая бы­строту изменения скорости точки во времени.

П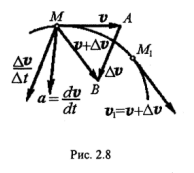усть точка в момент времени t находится в положении М и имеет скорость v(t), а в момент t₁=t + ∆t приходит в поло­жение М₁ и имеет скорость v₁ (рис. 2.8). Тогда за промежуток времени ∆t= t₁-t вектор скорости получает векторное прираще­ние ∆v = v₁-v , которое определяет изменение вектора скорости и по величине и по направлению. Для определения приращения скорости ∆v перенесем вектор v₁ параллельно своему направлению в точку М. Далее, соединив концы векторов v и v₁, получим ∆v. Разделив вектор ∆v на соответствующий промежуток време­ни ∆t, получим вектор

Таким образом, ускорение точки в данный момент вре­мени, есть векторная величина, равная первой производной от вектора скорости или второй производной от радиус-вектора по времени.

Установим теперь положение вектора ускорения a отно­сительно траектории. Отметим, что плоскость треугольника МАВ, образованного векторами v, v₁, ∆v , при ∆t →0 будет поворачи­ваться вокруг вектора v, т.е. вокруг касательной к траектории в точке М, и в пределе займет определенное предельное положе­ние. Это предельное положение плоскости МАВ называется соприкасающейся плоскостью в точке М траектории. Для плоской кривой эта плоскость есть плоскость самой кривой.

Как видно из рис. 2.8, вектор среднего ускорения а_ср на­правлен так же, как и ∆v, т.е. в сторону вогнутости траектории точки, и все время находится в плоскости треугольника МАВ.

Предел вектора а_ср при ∆t →0 есть вектор а, который расположен в предельном положении треугольника МВА, т.е. в соприкасаю­щейся плоскости траектории точки М. Итак, вектор полного ус­корения точки находится в соприкасающейся плоскости траек­тории точки и направлен в сторону вогнутости траектории.

6. УСКОРЕНИЕ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ

Рассмотрим движение точки М относительно неподвиж­ной прямоугольной декартовой системы координат (см. рис. 2.5). В этом случае ее движение задано следующим образом:

x = x(t) y = y(t) z = z(t) (1)

Разложим радиус-вектор точки по ортам осей Oxyz:

r = x(t)i + y(t)j + z(t)k (2)

Дифференцируя равенство (2) дважды по времени, получим:

или

Т.е. проекции вектора ускорения на неподвижные оси координат равны первым производным по времени от соответ­ствующих проекций вектора скорости или вторым производным от соответствующих координат точки.

По этим проекциям определяем величину и направление вектора ускорения:

или

7. ЕСТЕСТВЕННЫЙ КООРДИНАТНЫЙ ТРЕХГРАННИК

Рассмотрим пространственную кривую. Предельное по­ложение секущей, проходящей через точки М и M₁ кривой, когда точка M₁ стремится к точке М, называется касательной к кри­вой в данной точке М. Перпендикуляр к касательной в точке М называется нормалью к кривой в этой точке. Геометрическое место нормалей к данной кривой в данной точке называется нормальной плоскостью. Линия пересечения нормальной и сопри­касающейся плоскостей называется главной нормалью. Нормаль, перпендикулярная главной нормали, называется бинормалью.

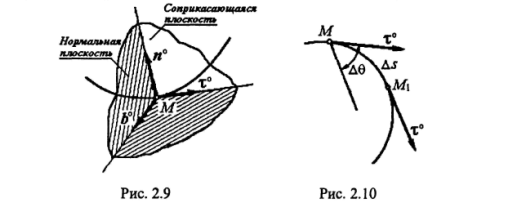
Обозначим единичные векторы: касательной через τ°, главной нормали n° и бинормали b°. Через эти векторы проходят плоскости: (τ°, n°) - соприкасающаяся, (n°, b°) - нормальная и (b°, τ°) - спрямляющая. Три взаимно перпендикулярных направ­ления, которые определяются векторами τ°, n° и b°, образуют ес­тественную систему координат, или так называемый естествен­ный, или подвижный, трехгранник. Направление τ°, n° и b° определяются так же, как направление координатных осей, т.е. по правой системе, при этом единичный вектор главной нормали всегда направлен в сторону вогнутости кривой (рис. 2.9).

Проведем теперь в двух точках кривой М и М₁ единич­ные векторы касательных τ° и τ°₁ .Угол между этими касательны­ми называется углом смежности. Обозначим этот угол через ∆θ, а длину дуги ММ₁ через ∆s (рис. 2.10). Предел отношения ∆θ и ∆s при ∆s0, т.е.

, называется кривизной кривой в данной точке M. (1)

Найдем кривизну окружности радиу­са R. Возьмем на окружности дугу АВ = ∆s и проведем в точках А и В касательные к окружности (рис. 2. 11). Тогда

(2)

Отсюда следует, что окружность представляет собой кривую линию постоянной кривизны, равной обратной величине ее радиуса. Кривизна произвольной кривой вообще не­постоянна. Если через три точки М, М₁ и М₂ кривой провести ок­ружность, то в пределе при приближении точек М₁ и М₂ к М по­лучим предельную окружность, лежащую в соприкасающейся плоскости, которая называется кругом кривизны (рис. 2.12).

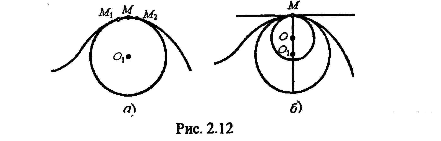Центр круга кривизны называется центром кривизны, а радиус этого круга — радиусом кривизны кривой в точке М. Вели­чина, обратная кривизне, называется радиусом кривизны данной кривой в данной точке.

Обозначая радиус кривизны буквой ρ, получим:

, .

8. РАЗЛОЖЕНИЕ УСКОРЕНИЯ ПО ЕСТЕСТВЕННЫМ ОСЯМ

Вектор скорости точки можно представить в виде: (1)

В правой части этого равенства с течением времени изменяются оба множителя: и проекция вектора скорости на касательную v_τ, и на­правление единичного вектора τ°. Дифференцируя равенство (1) по времени, получим:

(2)

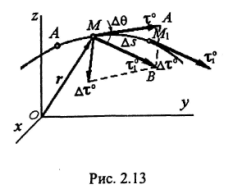
Первое слагаемое представляет собой вектор, направленный по касательной. Чтобы определить второе слагаемое, будем рас­сматривать вектор τ° как функцию дуговой координаты s. Тогда:

(3)

Вектор , входящий в равенство (3), всегда направлен в сторону вогнутости траектории точки и, как видно из рис. 2.13, лежит в соприкасающейся плоскости. Действительно, приращение вектора τ° (см. рис. 2.13) ∆ τ° =τ°₁ - τ° лежит в плоскости треугольника МАВ. Если точка М₁→ M, эта плоскость, вращаясь вокруг неподвижного вектора τ°, стремится к предельному положению, т.е. к соприкасающейся плоскости. Далее, дифференцируя тождество τ° ∙τ° = 1по s, получим:

(4)

а это есть условие перпендикулярности векторов сомножителей.

Таким образом, рассматриваемый вектор лежит в соприка­сающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен вектору τ°. Следовательно, он направлен по главной нормали к центру кривизны, т.е. по направлению орта n°. Поэтому

(5). Из треугольника МАВ: , откуда Переходя в последнем равенстве к пределу при ∆s→0, найдем:

, поэтому . Тогда окончательно:

П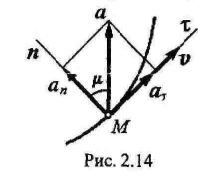одставляя найденное выражение вектора из (6) в равенстве (2) и учитывая, что v_τ²=v₂², получим: Эта формула представляет собой разложение ускорения точки М по ортам естественного трехгранника. Составляющие вектора ускорения по направлениям τ° и n° соответственно равны (рис. 2.14):

Проекция ускорения на направление касательной: называется касательным или тангенциальным ускорением. Проекция ускорения на главную нормаль: называется нормальным ускорением. Так как ускорение точки лежит в соприкасающейся плоскости, то проекция ускорения на бинормаль равна нулю. Модуль ускорения, на основании формул (9)-(10), будет

или 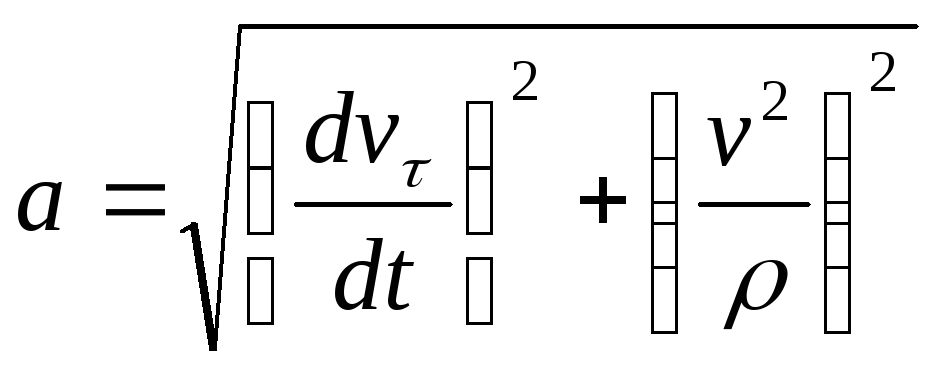. Угол между вектором a и главной нормалью можно определить так:

,

Касательное ускорение характеризует изменение скоро­сти по величине, а нормальное ускорение - изменение скорости по направлению.

Касательное ускорение равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, когда скорость достигает экстремальных значений. Если V_τ и a_τ одного знака, движение называется ускоренным, если же V_τ и a_τ разных знаков - замедленным. При a_τ =0 движение равномерное. Нор­мальное ускорение равно нулю при прямолинейном движении (ρ→∞), в точках перегиба криволинейной траектории и в моменты времени, когда скорость точки обращается в нуль.

В заключение отметим, что модули тангенциального и нормального ускорений также можно определить и в случае за­дания движения точки координатным способом.

В самом деле, вспоминая определения модулей скаляр­ного и векторного произведений и представляя единичный вектор касательной, определяемый формулой , запишем:

, , или

Значения этих выражений определяются непосредственно дифференцированием закона движения точки, заданного координатным способом.

10. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ

Разложение ускорения по естественным осям координат удобно для анализа и классификации различных случаев движе­ния точки.

Равномерное прямолинейное движение. Если во время движения точки ее ускорение равно нулю (а = 0), то такое дви­жение называется равномерным и прямолинейным. Скорость точки в этом случае не изменяется ни по величине, ни по направ­лению.

Прямолинейное переменное движение. Если во время движения точки ее нормальное ускорение равно нулю, то это движение прямолинейное. В самом деле, при а_n = 0, , а это

значит, что ρ→∞, т.е. траекторией точки является прямая.

Равномерное криволинейное движение. Если во время движения точки ее тангенциальное ускорение равно нулю (a_τ=0), то проекция скорости на касательную не изменяется. В этом слу­чае точка движется равномерно по кривой и ее полное ускорение равно нормальному, т.е. а = а_n .

Рис. 2.15

Равнопеременное криволинейное движение

Если во все время движения величина касательного ус­корения точки постоянна, т.е. a_τ = const, то криволинейное движение называется равнопеременным.

При этом следует помнить, что если направление a_τ сов­падает с направлением скорости, то движение называется равно­ускоренным, если же a_τ направлено в сторону, противоположную скорости, то - равнозамедленным (рис. 2.15).

Рассмотрим более подробно это движение. Найдем закон изменения скорости точки и ее закон движения по криволиней­ной траектории s = s(t), считая, что при t=0 s = s₀, а v= v₀.

Здесь s₀ - начальное расстояние от начала отсчета; v₀ - начальная скорость точки.

Тогда из выражения

, или ,

интегрируя, найдем закон изменения скорости точки

. Далее, принимая во внимание, что , и вторично

интегрируя, получим закон равнопеременного криволинейного движения:

.

Отметим, что формулы (2) и (3) отличаются от соответ­ствующих формул для случая прямолинейного движения точки тем, что в эти формулы входит касательное ускорение.

Рассмотрим теперь, как определяет­ся ускорение точки при ее движении по ок­ружности радиусом R (рис. 2.16).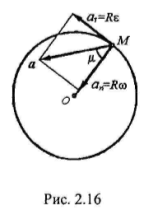

Скорость точки в случае ее движе­ния в положительном направлении отсчета расстояний определим по полученной выше формуле:

(4)

Дифференцируя это равенство по времени, получим касательное ускорение:

.

Величина:

называется угловым ускорением вращения радиуса OM=R.

Нормальное ускорение получим, принимая во внимание, что радиус кривизны окружности равен ее радиусу, т. е. ρ = R:

Модуль ускорения точки в круговом движении

Угол μ, который образует ускорение с радиусом окружности, определяется из равенства

Если V=const, то ускорение в круговом движении будет направлено по радиусу, так как тангенциальное ускорение в этом случае равно нулю.

11. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

Поступательным движением твердого тела называет­ся такое движение, при котором любая прямая, проведенная в теле во все время движения, остается параллельной своему первоначальному направлению.

При поступательном движении точки тела могут дви­гаться по любым траекториям. Рассмотрим движение тела отно­сительно некоторой системы координат (рис. 2.19). Возьмем в теле точку А. Векторное уравнение движения точки А имеет вид:

r_A = r_A(t).

Возьмем в теле другую точку В, определяемую радиус-вектором r_B. Векторное уравнение движения точки В имеет вид:

r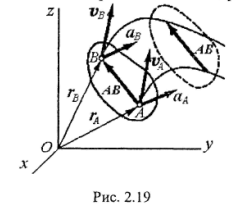_B = r_A+AB

При движении тела радиус-векторы r_A и r_B изменяются с течением времени и по модулю, и по направлению. Вектор АВ имеет постоянный модуль и по­стоянное направление, что следует из определения абсолютно твердо­го тела и его поступательного движения. Как видно из уравнения (2), траекторию точки В можно получить параллельным перено­сом траектории точки А. Направ­ление и величина этого переноса определяются вектором АВ.

Таким образом, при по­ступательном движении твердого тела все его точки описыва­ют одинаковые траектории, которые при параллельном перено­се совпадают.

Дифференцируя равенство (2) по времени, найдем:

Далее, учитывая, что , а вектор АВ не изменяется во времени ни по величине, ни по направлению, и следовательно, производная , имеем

V_B=V_A

При вторичном дифференцировании:

a_B=a_A

Так как точки А и В были выбраны произвольно, то фор­мулы (4) и (5) показывают, что при поступательном движении все точки твердого тела движутся с одинаковыми скоростями и ускорениями для любого момента времени.

Из этих свойств поступательного движения следует, что изучение поступательного движения тела сводится к изучению движения какой-либо одной из его точек. Следовательно, при изучении поступательного движения твердого тела можно при­менять все формулы, рассмотренные выше при исследовании движения одной точки.

12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают кон­центрические окружности, центры которых лежат на одной прямой, называемой осью вращения.

Р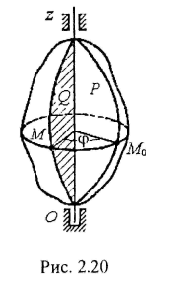ассмотрим вопрос о зада­нии уравнения, или закона вращательного движения. Пусть ось Oz является неподвиж­ной осью, вокруг которой вращается тело. Проведем через ось Oz две плоскости: под­вижную Р и неподвижную Q (рис. 2.20). По­ложение вращающегося тела может быть опре­ делено двугранным углом φ между этими плос­костями. Назовем угол φ углом поворота тела и условимся считать положительным, если, глядя с положительного конца оси z, угол φ виден отложенным от неподвижной плоскости против хода часовой стрелки. Угол поворота тела обычно измеряют в радианах. Иногда в практических задачах этот угол выражают числом оборотов N тела. Так как один оборот тела соответствует 2π радиан, то получаем зависимость

φ =2π N (1)

При вращении тела угол поворота изменяется с течением времени, т.е.

φ = φ (t) (2)

Равенство (2) называется уравнением, или законом вра­щательного движения твердого тела вокруг неподвижной оси.

Рассмотрим теперь основные кинематические величины, характеризующие вращательное движение тела. Этими величи­нами являются угловая скорость тела ω и угловое ускорение ε.

Угловой скоростью тела называется физическая величина, характеризующая быстроту изменения угла поворота φ тела во времени, т.е.:

(3)

В самом деле, пусть за промежуток времени ∆t угол по­ворота φ получил приращение ∆φ. Тогда средняя угловая ско­рость определится равенством:

(4)

Предел этого отношения при ∆t→0 называют угловой скоростью тела в данный момент времени

(5)

Мы вновь пришли к равенству (3). Итак, угловая ско­рость тела равна первой производной по времени от угла пово­рота тела. Значение угловой скорости ω для данного момента времени может быть положительным или отрицательным в зави­симости от того, возрастает или убывает угол поворота тела.

Если ω > 0, то тело в данный момент времени вращается в положительном направлении отсчета угла поворота φ, т. е. про­тив движения часовой стрелки.

Размерность угловой скорости [ω]=с^-1. В технике угло­вую скорость характеризуют числом оборотов в минуту и обо­значают буквой n. Замечая, что n об/мин соответствует n/60 об/с и что 1 оборот соответствует 2π радианам, получим:

c^-1 (6)

Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к приращению времени:

(7)

Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к прираще­нию времени:

(8)

Таким образом, угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скоро­сти или второй производной от угла поворота.

Размерность углового ускорения [ε] = с^-2. Если знаки уг­ловой скорости и углового ускорения одинаковы, то вращение тела в данный момент ускоренное, если же знаки ω и ε различны, вращение замедленное.

13. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

Вращение тела называют равномерным, если угловая скорость тела постоянна, т.е. ω =const.

В этом случае:

(1)

Произвольную постоянную С определяем из начального условия . В результате находим С = φ_0. Тогда:

φ = φ₀ + ωt (2)

Равенство (2) называется законом равномерного враща­тельного движения твердого тела. При φ₀=0 это равенство уп­рощается.

Равнопеременным вращением называется такое враща­тельное движение тела, при котором его угловое ускорение по­стоянно, т.е. ε = const ≠ 0. В этом случае:

, , (3)

Из начального условия находим С₁ = ω_0. Тогда ω = ω₀ + εt (4)

Равенство (4) называется законом изменения угловой скорости при равнопеременном вращательном движении тела. Далее

, , (5)

Из начального условия находим С₂ = φ₀.

Тогда окончательно

(6)

Равенство (6) называется законом равнопеременного вращательного движения твердого тела. Легко заметить анало­гию между полученными формулами (2) и (6) и формулами рав­номерного и равнопеременного движения точки. Соответствую­щие формулы совпадают с точностью до обозначений.

14. СКОРОСТЬ ТОЧЕК, ВРАЩАЮЩИХСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ

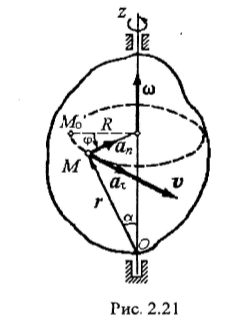
Пусть вращение тела вокруг неподвижной оси задано уравнением

(1)

Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естест венным способом за­дания движения точки. Рассмотрим движение какой-нибудь точ­ки М тела. При вращении тела точка М будет описывать окруж­ность, радиус которой обозначим R (рис. 2.21).

Составим уравнение движения точки М по ее траекто­рии. За начало отсчета примем начальное положение М₀, а за по­ложительное направление дуги s - направ­ление отсчета угла поворота φ. Тогда урав­нением движения точки М по ее траектории будет

S = M₀M = Rφ (2)

а следовательно, проекция скорости точки М на направление касательной определится следующим образом:

(3) или

(4)

Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Та­ким образом, линейная скорость какой-либо точки вращающего­ся твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Вектор v скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль v вектора скорости v равен

. (5)

Так как угловая скорость ω является кинематической ха­рактеристикой всего тела в целом, то из формулы (5) следует, что скорости точек тела пропорциональны расстояниям этих точек до оси вращения.

15. УСКОРЕНИЕ ТОЧЕК, ВРАЩАЮЩИХСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Ускорение точки М находим, определив сначала каса­тельное и нормальное ускорения:

(6)

Тогда модуль полного ускорения точки М:

(7)

Угол, образованный вектором ускорения точки М с ра­диусом описываемой точкой окружности, определяется так:

(8)

Из формулы (8) следует, что ускорения точек вращающе­гося тела образуют в данный момент один и тот же угол α с ра­диусами описываемых ими окружностей. В частном случае рав­номерного вращения ε=0, поэтому α=0 и, следовательно, полное ускорение по модулю равно нормальному и направлено к оси вращения.

16. векторная формула для скорости точек тела, вращающихся вокруг неподвижной оси

Рассмотрим твердое тело, вращающееся вокруг непод­вижной оси Oz с угловой скоростью . Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с те­лом (рис. 2.22). В этом случае

r = x(t)i + y(t)j + z(t)k (1)

Здесь следует заметить, что в разло­жении (1) х, у, z и вектор к постоянны, т.е. не зависят от времени, а i и j зависят от времени, так как вращаются вместе с телом.

Тогда для скорости точки М имеем

(2)

Производные от единичных векторов, входящие в формулу (2), есть скорости концов этих векторов. Например, при φ > 0 вектор скорости конца i направлен парал­лельно j в положительном направлении оси Оу, а вектор скорости конца j направлен параллельно i в отрицательном направлении оси Ох. Модуль каждой из этих скоростей равен .

Тогда ,

Далее, учитывая, что , а , получим

, а (3)

Подставляя формулы (3) в равенство (2) и используя то, что , найдем:

(4)

Назовем вектор вектором угловой скорости ω, тогда . (5)

Как видно из равенства (5), вектор угловой скорости те­ла направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца, видел вращение тела против хода часо­вой стрелки.

Вектор со можно расположить в любом месте оси враще­ния, т.е. СО - скользящий максиальный вектор.

Перепишем теперь формулу (4) с учетом (5), тогда

(6)

Вектор скорости любой точки тела, вращающегося во­круг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведен­ный из произвольного центра, взятого на оси вращения.

Формула (6) называется формулой Эйлера.

Примечание. Так как , то из (6) следует, что если

вектор r изменяется со временем только по направлению, то

, (а)

где ω - угловая скорость поворота вектора r. Формула (а) опре­деляет правило дифференцирования вектора, постоянного по модулю. Аналогично из равенств (3) и (5) получаем:

(б)

Модуль скорости точки М:

(7),

что совпадает с формулой (5) по времени, получим вектор углового ускорения:

(8)

Вектор углового ускорения ε, так же как и вектор угло­вой скорости ω, лежит на оси вращения. При этом в случае ус­коренного вращения вектор ε направлен в ту же сторону, что и вектор ω, в случае же замедленного вращения вектор ε направлен в сторону, противоположную вектору ω.

Для определения проекций скорости точки М на оси вы­бранной подвижной системы координат представим формулу (6) в виде определителя третьего порядка:

. (9)

Отсюда:

, , . (10)

Равенства (10) определяют проекции скорости любой точки М вращающегося тела на выбранные оси координат.

Выведем теперь векторную формулу для определения ускорения произвольной точки М тела, вращающегося вокруг неподвижной оси. Для этого продифференцируем равенство (6) по времени. В результате получим

(11) , или (12)

Из рис. 2.23 видно, что вектор направлен по каса­тельной к траектории, а вектор - по радиусу МО₁, т.е. по главной нормали к траектории. Следовательно,

, (13)

Из формул (13) находим:

Т.е. приходим к известным ранее равенствам. Далее, если взять систему осей координат Oxyz, в которой ось z направлена вдоль оси вращения, и представить a_n в виде a_n=-ω²∙O₁M, то, согласно (12) и (13)

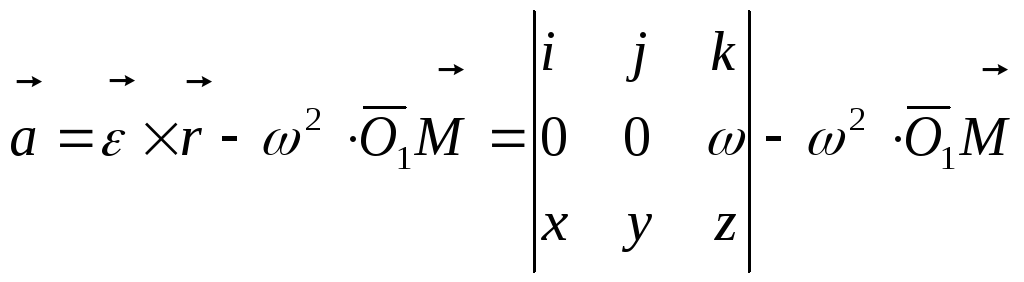(14)

Отсюда получаем:

, , . (15)

Равенства (15) дают проекции ускорения любой точки М(х, у, z) вращающегося тела на выбранные оси координат.