2. Метод трапеций

Метод трапеций является одним из методов численного интегрирования. Он позволяет вычислять определенные интегралы с заранее заданной степенью точности.

Поставим перед собой следующую задачу: пусть нам требуется приближенно вычислить определенный интеграл 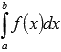, где подынтегральная функцияy=f(x) непрерывна на

отрезке [a;b].

Разобьем отрезок [a;b] на n равных интервалов длины h точками . В этом случае шаг разбиения находим каки узлы определяем из равенства.

Рассмотрим подынтегральную функцию на элементарных отрезках .

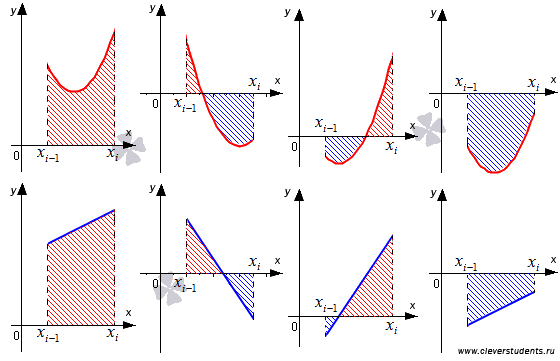
Возможны четыре случая (на рисунке показаны простейшие из них, к которым все сводится при бесконечном увеличении n):

На каждом отрезке заменим функциюy=f(x) отрезком прямой, проходящей через точки с координатами и. Изобразим их на рисунке синими линиями:

В качестве приближенного значения интеграла возьмем выражение, то есть, примем.

Давайте выясним, что означает в геометрическом смысле записанное приближенное равенство. Это позволит понять, почему рассматриваемый метод численного интегрирования называется методом трапеций.

Мы знаем, что площадь трапеции находится как произведение полу суммы оснований на высоту. Следовательно, в первом случае площадь криволинейной трапеции приближенно равна площади трапеции с основаниями и высотойh, в последнем случае определенный интеграл приближенно равен площади трапеции с основаниямии высотойh, взятой со знаком минус. Во втором и третьем случаях приближенное значение определенного интеграла 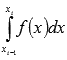равно разности площадей красной и синей областей, изображенных на рисунке ниже.

Таким образом, мы подошли к сути метода трапеций, которая состоит в представлении определенного интеграла в виде суммы интегралов видана каждом элементарном отрезке и в последующей приближенной замене.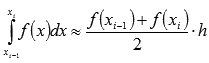

Формула метода трапеций.

В силу пятого свойства определенного интеграла .

Если вместо интегралов подставить их приближенные значения, то получитсяформула метода трапеций:

Оценка абсолютной погрешности метода трапеций.

Абсолютная погрешность метода трапеций оценивается как.

Графическая иллюстрация метода трапеций.

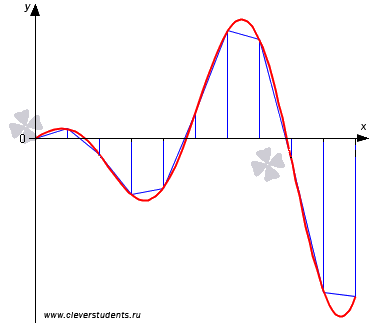
3. Метод Симпсона (парабол)

Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и нам требуется вычислить определенный интеграл .

Разобьем отрезок [a; b] на n элементарных отрезков длиныточками. Пусть точкиявляются серединами отрезковсоответственно. В этом случае все "узлы" определяются из равенства.

Суть метода парабол.

На каждом интервале подынтегральная функция приближается квадратичной параболой, проходящей через точки. Отсюда и название метода - метод парабол.

Это делается для того, чтобы в качестве приближенного значения определенного интеграла взять, который мы можем вычислить по формуле Ньютона-Лейбница. В этом и заключаетсясуть метода парабол.

Геометрически это выглядит так:

Графическая иллюстрация метода парабол (Симпсона).

Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.

Вывод формулы метода Симпсона (парабол).

В силу пятого свойства определенного интеграла имеем .

Для получения формулы метода парабол (Симпсона) нам осталось вычислить .

Пусть (мы всегда можем к этому прийти, проведя соответствующее геометрическое преобразования сдвига для любогоi = 1, 2, ..., n).

Сделаем чертеж.

Покажем, что через точки проходит только одна квадратичная парабола. Другими словами, докажем, что коэффициентыопределяются единственным образом.

Так как - точки параболы, то справедливо каждое из уравнений системы

Записанная система уравнений есть система линейных алгебраических уравнений относительно неизвестных переменных . Определителем основной матрицы этой системы уравнений является определитель Вандермонда, а он отличен от нуля для несовпадающих точек. Это указывает на то, что система уравнений имеет единственное решение (об этом говорится в статье решение систем линейных алгебраических уравнений), то есть, коэффициентыопределяются единственным образом, и через точкипроходит единственная квадратичная парабола.

Перейдем к нахождению интеграла .

Очевидно:

Используем эти равенства, чтобы осуществить последний переход в следующей цепочке равенств:

Таким образом, можно получить формулу метода парабол:

Формула метода Симпсона (парабол) имеет вид .

Оценка абсолютной погрешности метода Симпсона.

Абсолютная погрешность метода Симпсона оценивается как