4.13. Определение функции вGpss

В GPSS рассматриваются пять типов функций:

1) дискретная числовая (D),

2) непрерывная числовая (С),

3) табличная числовая (L),

4) дискретная атрибутивная (Е),

5) табличная атрибутивная (М).

Рассмотрим два первых типа функций.

Дискретная функция представляет собой кусочно-постоянную функцию, которая состоит из горизонтальных ступеней (рис. 4.2). Непрерывная функция представляет собой кусочно-непрерывную функцию. Непрерывная функция в GPSS состоит из соединенных между собой прямых отрезков и представляет собой ломаную линию (рис. 4.3). Чтобы задать дискретную функцию, необходимо задать ко­ординаты крайних правых точек горизонтальных отрезков. Для не­прерывной функции необходимо задать координаты всех точек, кото­рые являются концами отрезков.

Действия, необходимые для определения дискретной и не­прерывной GPSS-функции:

1. Присвоить функции имя. Имя может быть числовым либо символьным.

2. Задать аргумент функции. Аргументом могут быть:

1) ссылка на генератор случайных чисел, используемый для ро­зыгрыша в соответствии с распределением, заданным функцией;

2) стандартный числовой атрибут;

3) ссылка на любую другую функцию.

В первом случае аргумент задается в виде RNj, j - целое число (номер генератора). В GPSS/PC; = 1,..., 7, т.е. возможно обращение к семи идентичным генераторам случайных чисел. При этом генерато­ры выдают случайные числа в диапазоне 0... 0,999. В GPSS World количество генераторов случайных чисел неограниченно, а выдаваемые ими значения 0... 0,999999.

3. Задать тип функции и число крайних точек функции.

4. Задать значения аргумента (переменной) и соответствующие значения функции (т.е. координаты крайних точек функции).

Три первых элемента информации указываются в операторе определения функции. Формат оператора представлен в таблице.

Таблица 4.21

За каждым оператором описания FUNCTION следуют операто­ры задания координат точек функции (значений аргументов Х_i и со­ответствующих им значений функции Y_i,) - это операторы описания координат функции. Их формат:

1) если координаты всех точек расположены в одной строке оператора описания функции:

2) если координаты точек расположены в нескольких операто­рах описания функции:

где Х_i и Y_i - координаты i-й точки функции (в случае моделирования случайной величины Х_i является i-и суммарной (кумулятивной) час­тотой, Y_i - соответствующим значением случайной величины).

Особенности оператора описания координат функции:

1) основной единицей информации оператора описания коорди­нат функции является пара значений Х_i ,Y_i (координаты точки i);

2) значения координат Х_i и Y_i одной точки функции разделяются запятой;

3) последовательные наборы координат разделяются знаком «/»;

4) координаты Х_i и Y_i относящиеся к одной точке, задаются од­ним оператором, т.е. пара координат одной точки не должна разры­ваться;

5) все строки описания координат функции должны начинаться с первой позиции;

6) во всех случаях значения аргумента должны удовлетворять следующим неравенствам:

Значение функции является ее стандартным числовым атрибу­том. Способ ссылки на этот атрибут зависит от того, как задано имя функции: в символьном или числовом виде. Если имя числовое, то к значению функции обращаемся через FNj (где j - номер функции), если имя символьное - через FN$<имя функции>.

1. Аргументом функции может быть и значение какой-либо другой функции.

2. Каждая функция должна иметь, по крайней мере, две описанные точки.

Пример 4.18

Пусть необходимо смоделировать дискретную случайную пере­менную, заданную в табл. 4.22.

Таблица 4.22

GPSS-функцию можно определить таким образом:

SERV FUNCTION RN4,D5

.15,2/.35,5/.6,8/.82,9/1,12

Графическая интерпретация функции показана на рис. 4.4.

Особенности вычисления дискретных и непрерывных GPSS-функций:

1. В начальной фазе выполняемые действия при вычислении дискретной и непрерывной функции одинаковы. При обращении к функции определяется значение ее аргумента. Потом просматривает­ся упорядоченный ряд значений X₁<X₂<...<Xi<...<X_n для определения интервала, в который попало значение аргумента (пусть это будет ин­тервал между точками i - 1 и i ).

2. Если функция дискретная, то второй элемент соответствую­щей пары X_i, Y_i является значением функции. Если функция непре­рывная, выполняется линейная интерполяция для пары точек i - 1 и i, находящихся на краях интервала значений функции, на который ука­зало значение аргумента. Целая часть результата интерполяции и является значением функции.

3. Если значение аргумента функции больше значения коорди­наты Х_n последней точки, то в обоих случаях (дискретной и непре­рывной функции) значениями функции являются значения Y_n.

Пример 4.19

Моделирование случайной переменной, равномерно распреде­ленной на интервале [2,5].

Эта случайная переменная может быть смоделирована функцией:

INN FUNCTION RN2,C2

0,2/1,6

Графическая интерпретация непрерывной функции показана на рис. 4.5.

Так как максимальное значение, которое может выдать генера­тор случайных чисел, равно 0,999, то фактические значения интерва­лов времени распределены равномерно на интервале [2, 5] и равны, соответственно, одному из значений: 2, 3, 4, 5. Если генератор выдаст число 0,999, функция, которая показана на рис. 4.5, примет значение 5,996, целая часть которого равна 5 (это и будет значением GPSS-функции INN). В случае, если генератор случайных чисел RN2 вы­даст значение 0,4, GPSS-функция INN примет значение 3 (см. рис. 4.5).

GPSS-функция INN не может принять значение, равное 6 (несмотря на то, что второй элемент второй пары оператора описания координат функции 0,2/1,6 равен 6).

Точные граничные значения RN2, соответствующие возможным значениям функции INN, представлены в табл. 4.23.

Таблица 4.23

Равномерное распределение [2, 3, 4, 5] не может быть задано непосредственно с помощью операндов А и В блока GENERATE. Здесь имеем четыре возможных значения, то­гда как интервал А ± В (А и В целые) всегда имеет нечетное число элементов.

Пример 4.20

Часто возникают ситуации, когда в процессе моделирования не­обходимо переходить в различные блоки программы в зависимости от логики работы модели. Стандартные блоки GPSS WORLD такие, как TEST (см. параграф 4.16) и TRANSFER, не всегда могут решить эту проблему, так как они позволяют распределять транзакты макси­мум по двум направлениям. В случае, когда осуществляется услов­ный переход на одну из нескольких меток (если более двух, то в обычных языках программирования используется оператор CASE OF), необходимо построить переключающую функцию. Для вызова переключающей функции используется блок TRANSFER в режиме безусловного перехода.

Пример переключающей функции:

PEREKL FUNCTION RN4,DS 0.2,LB1/0.4,LB2/0.6,LB3/0.8,LB4/1,LB5

GENERATE ,„100

TRANSFER ,FN$PEREKL

LB1 QUEUE STOR1

TERMINATE 0

LB2 QUEUE STOR2

TERMINATE 0

LB3 QUEUE STOR3

TERMINATE 0

LB4 QUEUE STOR4

TERMINATE 0

LB5 QUEUE STOR5

TERMINATE О

GENERATE 1

TERMINATE I

START 1

Переключающая функция построена на основе дискретной функции с тем отличием, что результатом функции являются метки. В этом примере переход осуществляется к одной из меток в зависи­мости от числа, которое получаем от генератора случайных чисел.

Моделирование неравномерных случайных величин. Ис­пользование функций в блоках GENERATE и ADVANCE. Пусть распределение интервалов поступления через определенный блок GENERATE или время задержки в некотором блоке ADVANCE не является равномерным (либо является равномерным с «плавающи­ми во времени», т.е. нефиксированными значениями среднего и по­ловины поля допуска). Для входов транзактов в модель через этот блок GENERATE и для задания закона времени задержки в соответ­ствующем блоке ADVANCE необходимо использовать функции и (или) СЧА. Использование функций, заданных в операндах блоков, зависит от контекста. От значения функции берется целая часть, за исключением тех случаев, когда это значение используется в качестве операнда В блоков GENERATE и ADVANCE или операнда С блока ASSIGN. В табл. 4.24 показаны различные варианты использования функций и СЧА в качестве операндов А и В блоков GENERATE и ADVANCE. Под результатом понимается значение интервала посту­пления или задержки.

Таблица 4.24

Пример 4.21

TIME FUNCTION RN3,D5 ,

.05,5/.15,6/.75,8/.93,9/1,10

К этой функции можно обратиться таким образом:

GENERATE FNSTIME

…

ADVANCE FNSTIME

Пример 4.22

Пусть в моделируемой системе время обслуживания некоторым устройством распределено равномерно на интервале А ± 2, где сред­нее время обслуживания А с вероятностью 0,4 принимает значение 5, а с вероятностью 0,6 - значение 7. Эту ситуацию можно смоделиро­вать следующим образом.

Определим функцию AVERAGET:

AVERAGE_T FUNCTION RN1,D2

.4,5/1,7

Используем ее в блоке ADVANCE:

ADVANCE FN$AVERAGE_T,2

Выполнение подпрограммы блока ADVANCE включает расчет функции AVERAGE_T. Это, в свою очередь, требует обращения к ге­нератору случайных чисел RN1. Пусть генератор выдал значение меньшее, чем 0,4. Тогда соответствующее значение функции AVERAGE_T равно 5. Таким образом, время задержки текущего транзакта в устройстве будет равномерно распределено на интервале 5±2.

Непрерывные случайные переменные, рассматриваемые как дискретные. Как известно, дискретные случайные переменные могут принимать только фиксированное число значений. В противо­положность этому, непрерывные (в классическом смысле этого тер­мина) случайные переменные могут иметь неограниченное число различных значений.

На практике обычно достаточно, чтобы все случайные перемен­ные имели конечное число конкретных значений. Нет необходимости в тщательном определении значений этих случайных переменных, за исключением случаев, когда необходимо делать расчеты с высокой степенью точности. Таким образом, вполне возможна дискретизация непрерывных распределений. После этого они могут быть определе­ны в GPSS с помощью дискретных и непрерывных GPSS-функций (непрерывные GPSS-функции по сути также являются дискретными, поскольку множество их значений дискретно и конечно).

Функции распределения случайных величин. В языке GPSS возможность задания функций распределения случайных величин ог­раничена заданием их в табличном виде путем аппроксимации непре­рывными функциями. Поэтому можно задать только те функции, ко­торые легко преобразовать для новых значений параметров. К таким функциям, например, относится функция экспоненциального распре­деления с параметром λ, = 1, а также функция стандартного нормаль­ного распределения с математическим ожиданием т = 0 и стандарт­ным отклонением σ =1.

Эти ограничения не касаются языка GPSS World, в котором для задания различных вероятностных функций распределения можно использовать библиотечные процедуры, написанные на языке PLUS. Однако использование вероятностных распределений в табличном виде значительно ускоряет процесс моделирования.

Моделирование пуассоновского потока. Рассмотрим таблич­ный способ задания пуассоновского потока заявок. Пуассоновский входящий поток описывается таким образом: вероятность поступле­ния k заявок пуассоновского потока в течение интервала t составляет

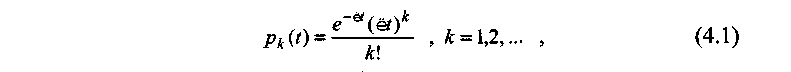
где λ - интенсивность потока.

Интервалы времени между соседними заявками пуассоновского потока распределены по экспоненциальному закону. Согласно ме­тоду обратной функции, можно получить ряд чисел, которые имеют экспоненциальное распределение, если ряд случайных чисел R, рав­номерно распределенных на интервале [0,1], преобразовать в соот­ветствии с функцией, обратной к экспоненциальной функции распре­деления:

где tj - 7-й разыгранный интервал времени поступления; Т= 1/λ, -средний интервал времени поступления; r_j - j-е число в последова­тельности случайных чисел R с равномерным распределением на ин­тервале [0, 1].

Разработчиками GPSS была осуществлена аппроксимация функции F^-1 (х), обратной к экспоненциальной функции распределе­ния с параметром λ= 1. Таким образом, функция F^-1 (х) была заме­нена 23 отрезками, которые использовались для преобразования значений RNj в значение - In(RNj).

Функция XPDIS определяет экспоненциальное распределение с интенсивностью λ= 1:

XPDIS FUNCTION RN1,C24 ; exponential distribution function 0,0/.l,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915/.7,1.2/ .75,1.38/.8,1.6/.84,1.83/.88,2.12/.9,2.3/.92,2.52/.94,2.81/ ,95,2.99/.96,3.2/.97,3.5/.98,3.9/.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

Пуассоновский входящий поток с интенсивностью λ, отличной от единицы, моделируется с помощью блока GENERATE таким об­разом:

1) в качестве операнда А используют среднее значение интервалов времени Т= λ/k, где λ - интенсивность пуассоновского потока;

2) в качестве операнда В используют СЧА - значение функции XPDIS, операторы определения и описания которой приведены выше.