
-Формула для поиска обратной матрицы, где
![]() - определитель матрицы
A
- определитель матрицы
A
![]()
![]() - алгебраические
дополнения элементов матрицы A
- алгебраические
дополнения элементов матрицы A
Они ищутся следующим образом:
![]()
![]()
![]()
![]()
Как запомнить формулу для обратной матрицы:
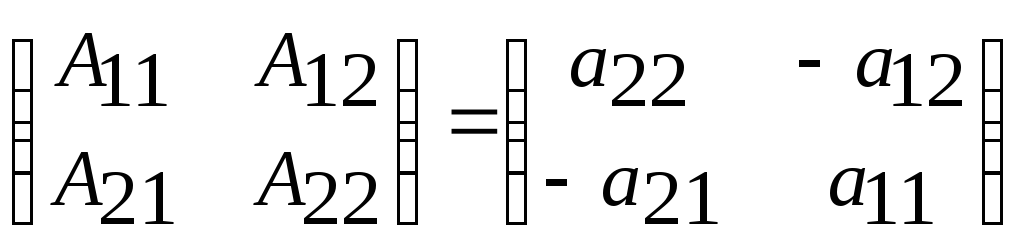 т.е. в исходной матрице надо поменять
местами элементы на главной диагонали,
а у двух оставшихся элементов изменить
знак на противоположный
т.е. в исходной матрице надо поменять
местами элементы на главной диагонали,
а у двух оставшихся элементов изменить
знак на противоположный
Найдем матрицу обратную к матрице
![]() (алгоритм описан выше)
(алгоритм описан выше)
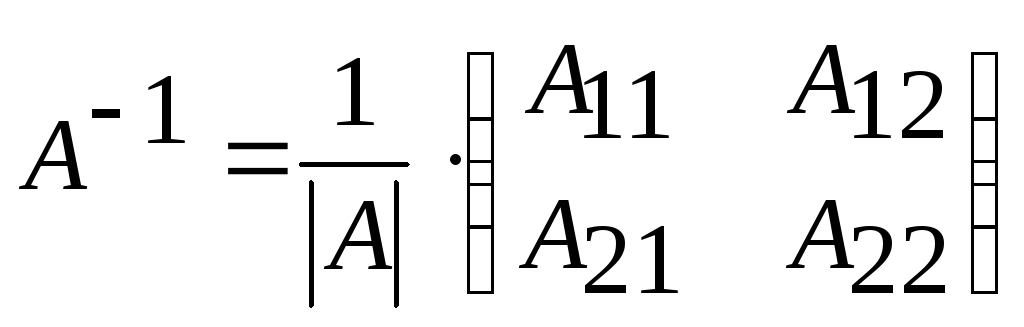
![]()
 = >
= >
![]() => обратная матрица существует
=> обратная матрица существует
Найдём алгебраические дополнения элементов матрицы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
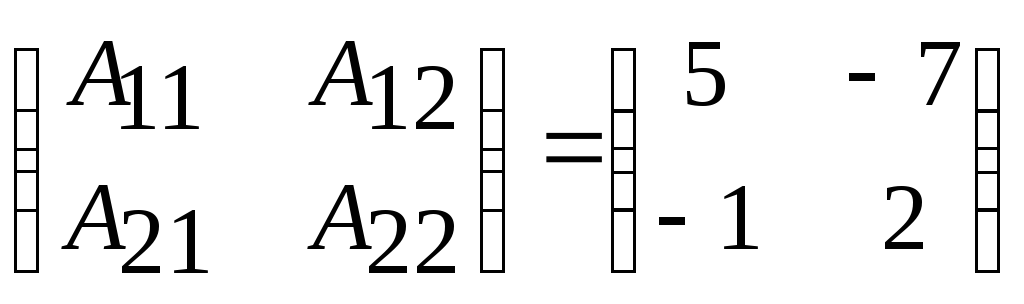 элементы на главной
диаг. переставили местами,
элементы на главной
диаг. переставили местами,
У оставшихся элементов поменяли знаки
![]()

Матричные уравнения:
Рассмотрим систему уравнений, состоящую
из 5 уравнений (![]() - неизвестные, остальные коэффициенты
– известные числа, цель найти неизвестные
- неизвестные, остальные коэффициенты
– известные числа, цель найти неизвестные
![]() )
)
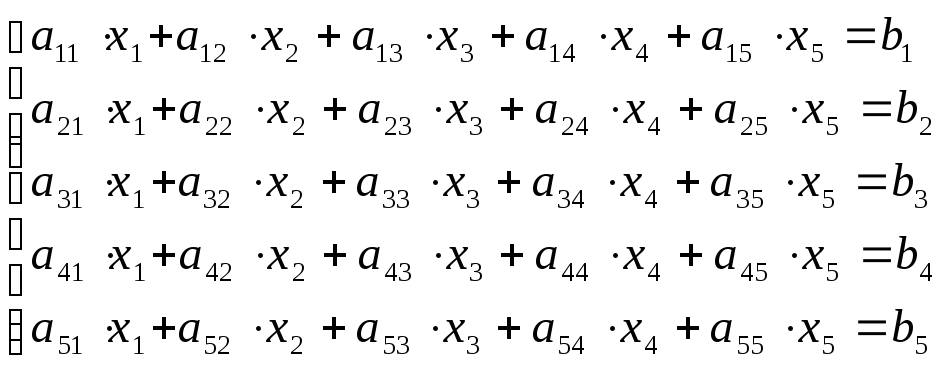 скалярная форма записи
скалярная форма записи
Используя матрицу
 ,
матрицу-вектор B=
,
матрицу-вектор B=![]()
и матрицу-вектор
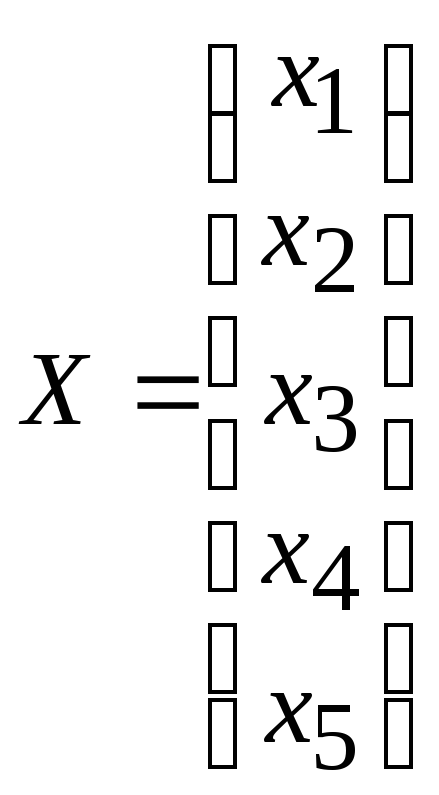 ,
,
можем записать систему уравнений в матричной форме :
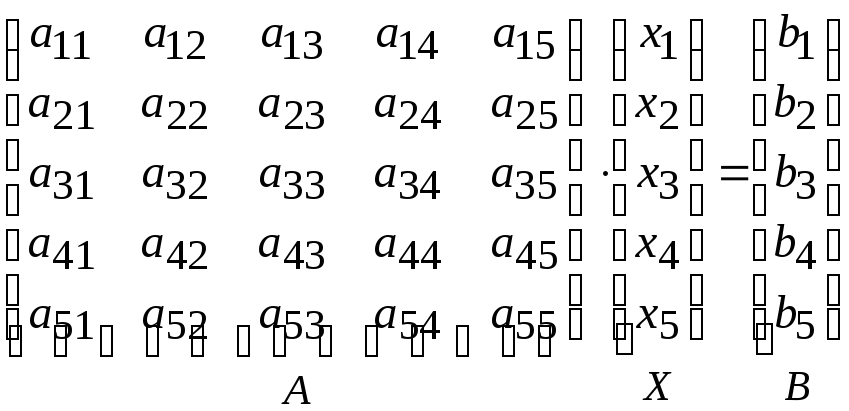
Или в сокращённой форме
![]()
Если обе части скалярного уравнения
![]() домножить на число
домножить на число
![]() (это
число обратное к
(это
число обратное к
![]() –
их произведение равно 1) то имеем
–
их произведение равно 1) то имеем
![]()
![]()
Возникает вопрос : как решать
матричное уравнение (будем использовать
метод решения основанный на умножении
на обратную матрицу - она является
аналогом обратного числа в матричном
случае, т.к.
![]() единичной
матрице
единичной
матрице
![]() - произведение двух матриц равно третьей;
A, B –
известные матрицы,
- произведение двух матриц равно третьей;
A, B –
известные матрицы,
![]() неизвестная матрица – её надо найти
неизвестная матрица – её надо найти
Домножим обе части уравнения на
![]() (обратную матрицу к матрице A)
слева
(обратную матрицу к матрице A)
слева
[!!! Это можно делать только в случае
если существует
![]() (т.е.
(т.е.
![]() )
– аналогично со скалярным уравнением
(см. выше)].
)
– аналогично со скалярным уравнением
(см. выше)].
![]()
![]() т.к.
т.к.
![]()
![]() т.к. (
т.к. (![]() => перемножив
=> перемножив
![]() и B найдём решение X
и B найдём решение X
Пример 1 (на метод обратной матрицы):
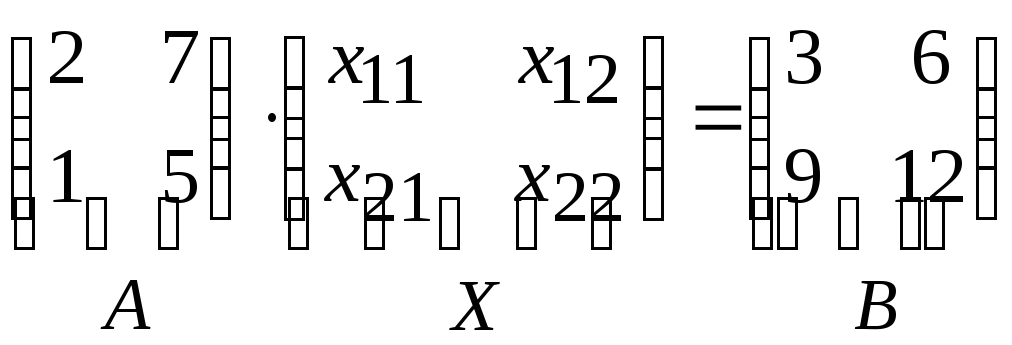 - матричное уравнение
- матричное уравнение
Найдем матрицу обратную к матрице A (алгоритм описан выше)
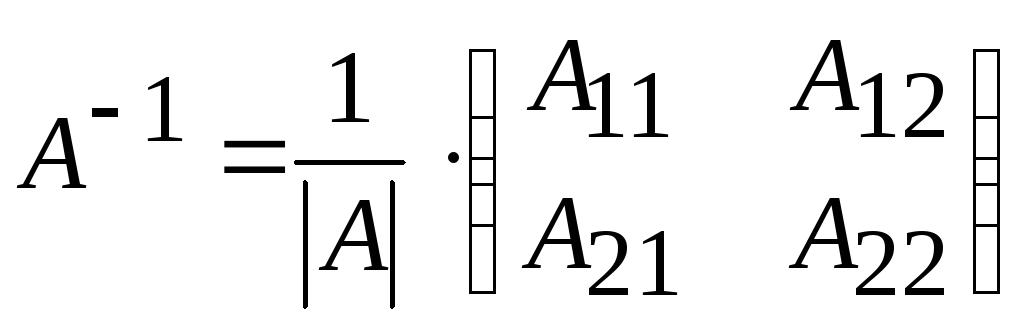
![]()
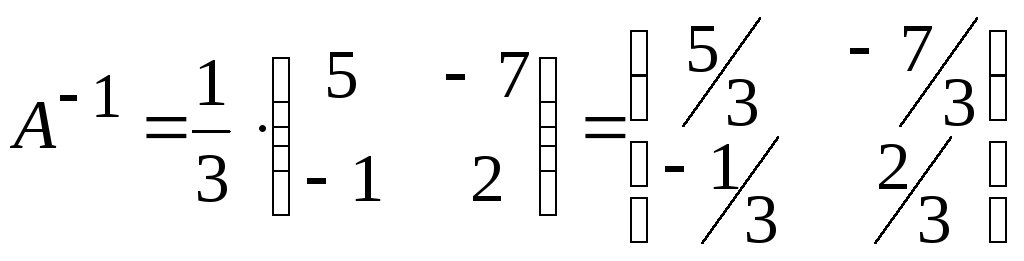
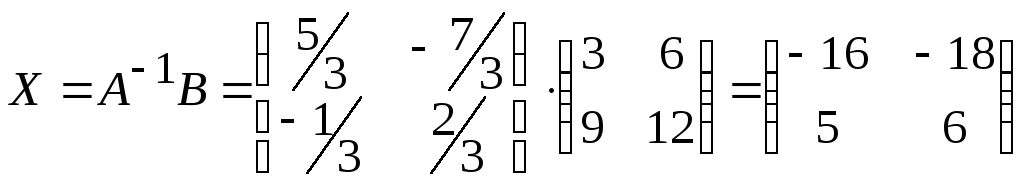
(см. Алгоритм перемножения матриц)
распишем подробно, как производится умножение:
![]()
![]()
![]()
![]()
Проверка
![]() (надо подставить полученную матрицу
(надо подставить полученную матрицу
![]() и
проверить, что действительно в результате
умножения получается матрица B)
и
проверить, что действительно в результате
умножения получается матрица B)
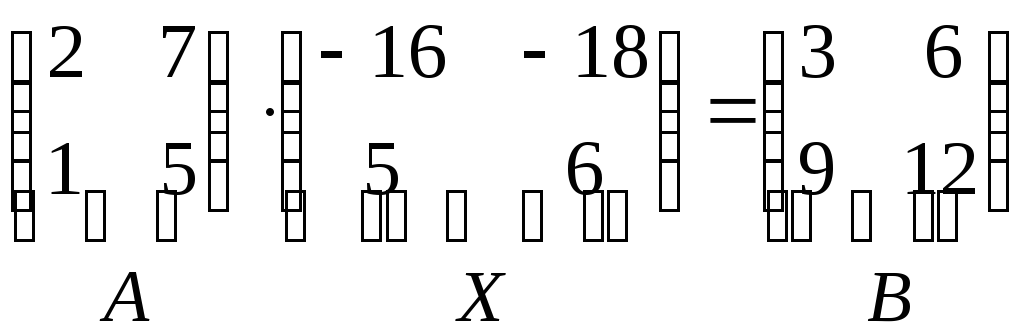 - убедиться самим, перемножив матрицы.
- убедиться самим, перемножив матрицы.
Пример 2 (на метод обратной матрицы):
Дано :
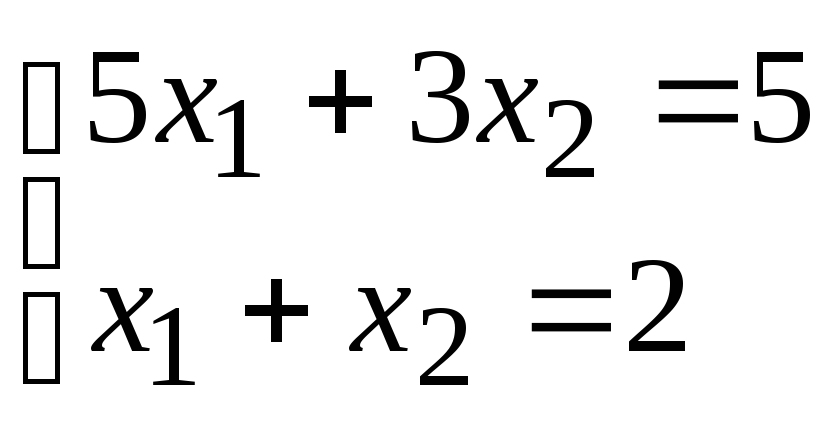 - система в скалярном виде. Найти решение
системы методом обратной матрицы
и сделать проверку, решив систему методом
Крамера
- система в скалярном виде. Найти решение
системы методом обратной матрицы
и сделать проверку, решив систему методом
Крамера
Запишем систему в матричном виде:
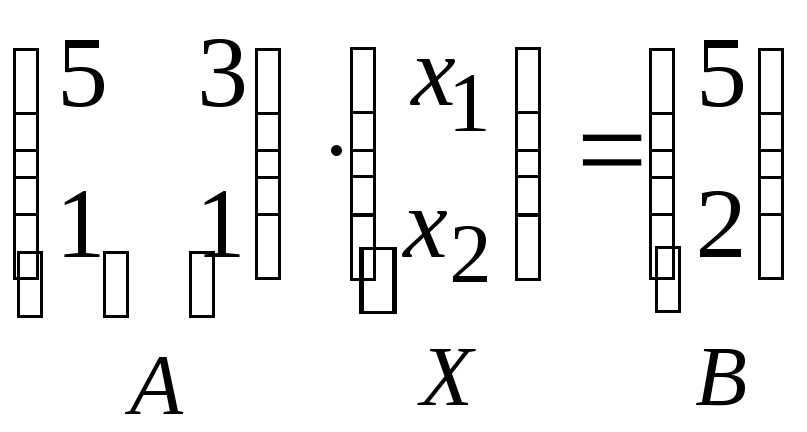 ,
где
,
где
![]() - матрица системы,
- матрица системы,
![]() - столбец свободных коэффициентов,
- столбец свободных коэффициентов,
![]() - столбец неизвестных
- столбец неизвестных
![]()
![]() -
матрица обратима (т.е. обратная матрица
существует)
-
матрица обратима (т.е. обратная матрица
существует)
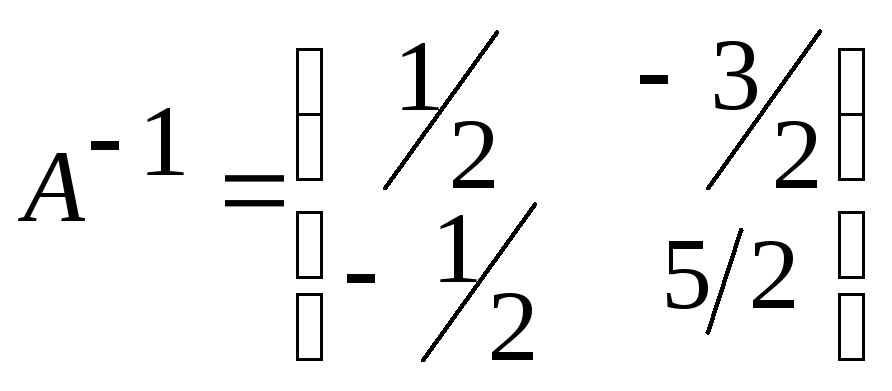 -обратная матрица ищется по алгоритму
описанному выше (проверить самим)
-обратная матрица ищется по алгоритму
описанному выше (проверить самим)
![]() - формула для поиска решения методом
обратной матрицы
- формула для поиска решения методом
обратной матрицы
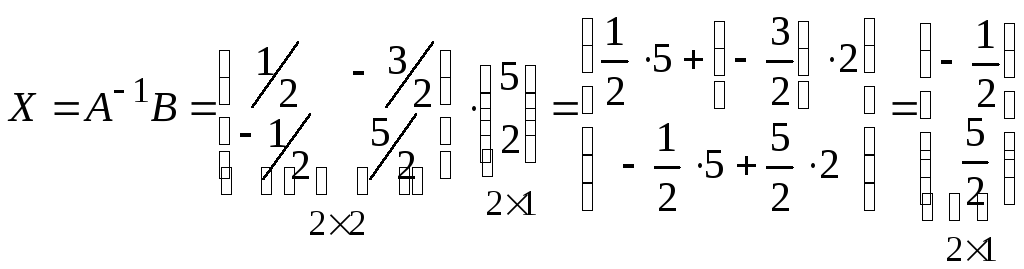
![]()
![]() - решение системы
- решение системы
ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ
Задача 1.
Предприятие производит продукцию трёх видов и использует сырьё двух типов. Норма затрат сырья на единицу продукции каждого типа задана матрицей
![]()
![]() -норма затрат сырья i-го
типа (кол-во единиц) на единицу продукции
j-го типа
-норма затрат сырья i-го
типа (кол-во единиц) на единицу продукции
j-го типа
Стоимость единицы сырья каждого типа задана матрицей- строкой
![]()
![]() - стоимость
единицы сырья j-го типа
- стоимость
единицы сырья j-го типа
![]()
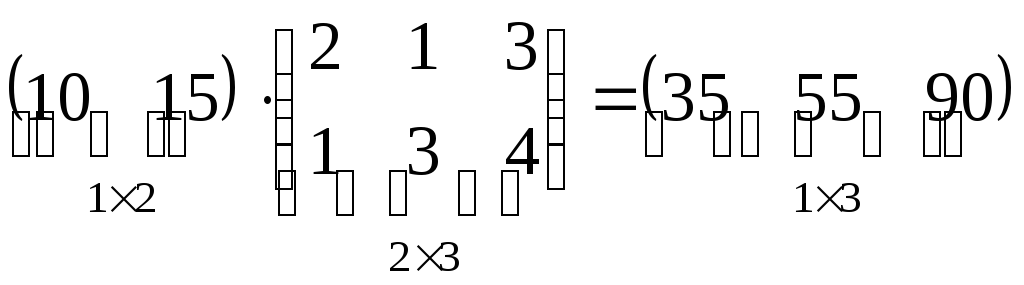 - получим матрицу-строку стоимости
единицы продукции каждого типа.
- получим матрицу-строку стоимости
единицы продукции каждого типа.
Обозначим полученную матрицу буквой C
![]()
Каковы общие затраты предприятия на производство 100 единиц продукции первого типа, 200 единиц продукции второго типа и 150 единиц продукции третьего типа.
Введём матрицу-вектор
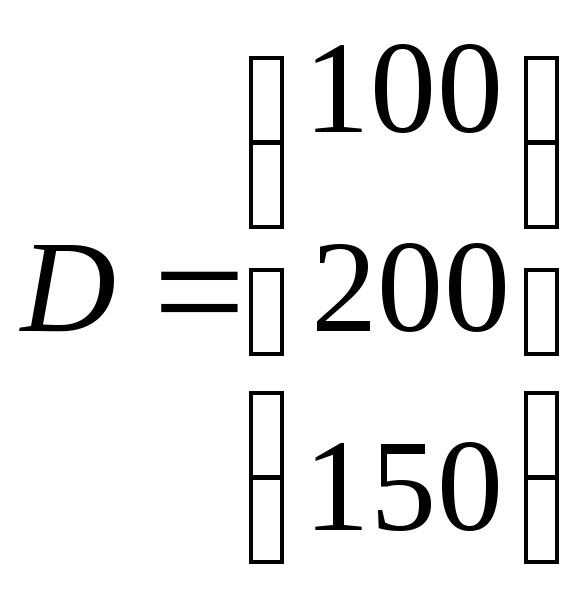 , который отражает необходимое количество
продукции каждого типа
, который отражает необходимое количество
продукции каждого типа
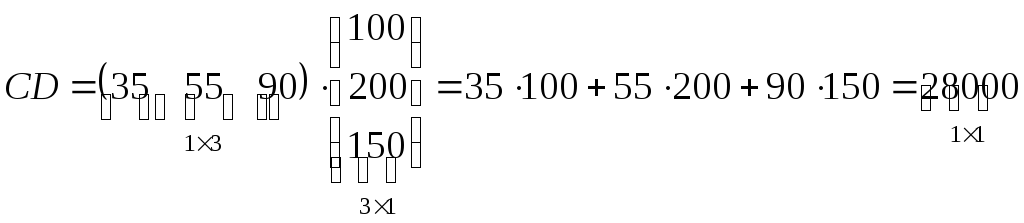 полные затраты рассчитаны
полные затраты рассчитаны
Задача 2.
Обувная фабрика специализируется по
выпуску изделий трёх видов: сапог,
кроссовок и ботинок, при этом используется
сырьё трёх типов
![]() .
Нормы расхода каждого из них на одну
пару обуви и объём расхода сырья на 1
день заданы таблицей:
.
Нормы расхода каждого из них на одну
пару обуви и объём расхода сырья на 1
день заданы таблицей:
|
Вид сырья |
Нормы расхода сырья на одну пару, усл.ед. |
Расход сырья на 1 день, усл. ед |
||
|
сапоги |
кроссовки |
ботинки |
||
|
S1 |
5 |
3 |
4 |
2700 |
|
S2 |
2 |
1 |
1 |
900 |
|
S3 |
3 |
2 |
2 |
1600 |
Найти ежедневный объём выпуска каждого вида обуви:
Решение:
Пусть ежедневно
фабрика выпускает
![]() пар сапог,
пар сапог,
![]() пар кроссовок и
пар кроссовок и
![]()
пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:
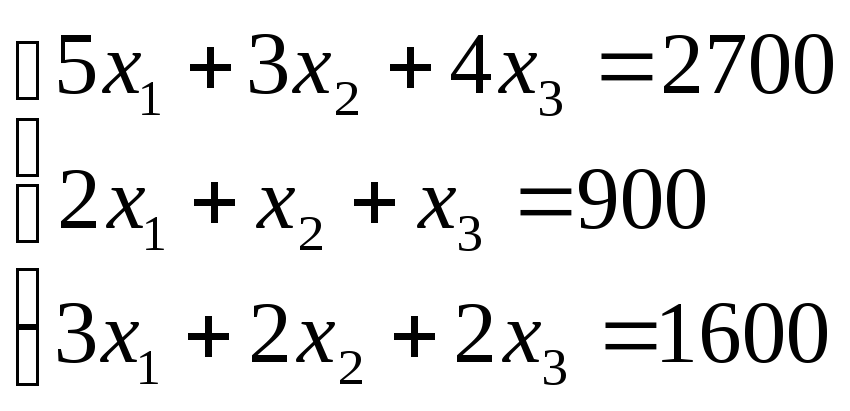 скалярная форма
скалярная форма
В матричном виде система выглядит следующим образом:
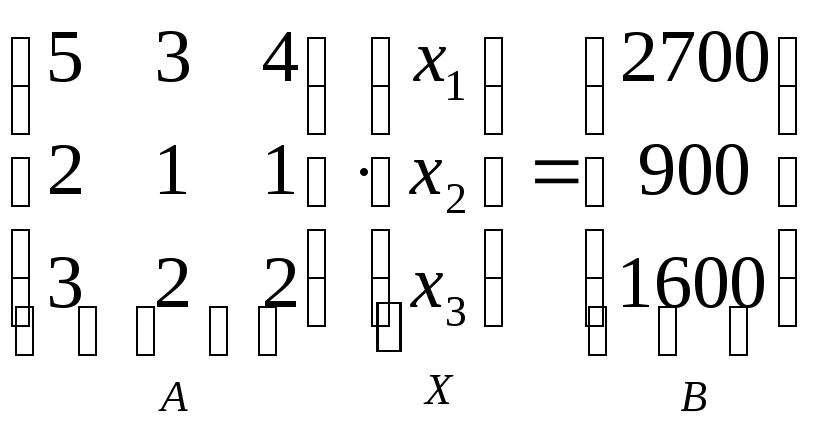 получаем матричное уравнение,
получаем матричное уравнение,
которое в сокращённом виде записывается как
![]()
можно его решить с помощью метода обратной матрицы, рассмотренного выше
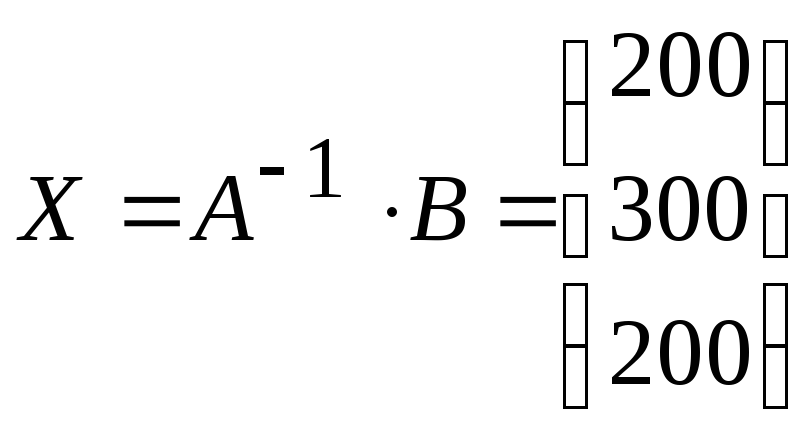 Следовательно, фабрика выпускает 200
пар сапог, 300 – кроссовок и 200 пар ботинок.
Следовательно, фабрика выпускает 200
пар сапог, 300 – кроссовок и 200 пар ботинок.
Можно это матричное уравнение решить с помощью метода Гаусса, который будет рассмотрен в следующей лекции.
