
МБИ, Высшая математика, Элементы алгебры матриц
Адрес сайта-www.Dariapiatkina.Narod.Ru/банковский интситут/высшая математика
Высшая математика
2 Семестр Лекция № 1.
Матрицы и действия над ними.
Введение.
Понятие матрицы и основанный на нём раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное - компактной матричной форме. Также понятие матрицы всем известно по одноимённому кинофильму Матрица. В компьютере файлы картинок хранятся в виде матриц. Форматы jpg, bmp кодируются матрицами. Обработка картинок в Photoshop – это матричная обработка. Раньше существовало такое понятие как матричный принтер. Таблицы Excel – это матричная форма представления результатов.
Матрица размера
![]() - прямоугольная таблица чисел, каждый
элемент которой имеет 2 индекса ( первый
- по строке и второй - по столбцу). Числа,
составляющие матрицу, называют элементами
матрицы. Матрицы
обозначаются большими латинскими
буквами A, B,
C, D и т.д.
Элементы матриц обозначаются маленькими
буквами с индексами.
- прямоугольная таблица чисел, каждый
элемент которой имеет 2 индекса ( первый
- по строке и второй - по столбцу). Числа,
составляющие матрицу, называют элементами
матрицы. Матрицы
обозначаются большими латинскими
буквами A, B,
C, D и т.д.
Элементы матриц обозначаются маленькими
буквами с индексами.
 матрица размера
матрица размера
![]()
Частные случаи:
![]() - матрица-строка (в матрице одна
строка)
- матрица-строка (в матрице одна
строка)
![]() - матрица-вектор (в матрице один
столбец)
- матрица-вектор (в матрице один
столбец)
Пример:
 матрица размера
матрица размера
![]()
![]()
![]()
![]() к каждому элементу можно обратиться
по его индексам (первый-строка,
второй-столбец)
к каждому элементу можно обратиться
по его индексам (первый-строка,
второй-столбец)
Если матрица имеет одинаковое число строк и столбцов, то она называется квадратной.
Пример:
 пример квадратной матрицы размера
пример квадратной матрицы размера
![]()
Квадратная матрица
 - у которой на главной диагонали 1, а вне
главной диагонали 0 называется единичной
- у которой на главной диагонали 1, а вне
главной диагонали 0 называется единичной
 - единичная матрица размера 3x3
- единичная матрица размера 3x3
Действия над матрицами
Над матрицами больших размеров действия вручную не производятся. Есть специальные компьютерные программы, которые используются для обсчёта матриц. Типичный пример матриц - это таблицы Excel.
Транспонирование –
это процедура, при применении которой
в матрице меняются местами строки и
столбцы. Транспонированная
матрица обозначается верхним индексом
«T». Если у исходной
матрицы размер
![]() ,
то у транспонированной матрицы размер
,
то у транспонированной матрицы размер
![]()
Пример:
 - исходная матрица (
- исходная матрица (![]()
 - транспонированная матрица
- транспонированная матрица
![]()
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ
Определитель матрицы – это число, характеризующее матрицу. Если определитель матрицы не равен 0, то говорят, что матрица невырожденная. В противном случае матрицу называют вырожденной. Определитель вычисляется только для квадратных матриц.
Определитель матрицы A
обозначают как
![]() (det A)
(det A)
Пусть матрица состоит из одного
элемента
![]() (т.е. имеет размер
(т.е. имеет размер
![]() )
)
В этом случае
![]()
Пусть матрица A
имеет размер
![]()

![]() для матрицы
для матрицы
![]() - определитель 2-го порядка
- определитель 2-го порядка
Как запомнить формулу для определителя втрого порядка: вычитание идет крест на крест по диагонали
Пример:
![]() (отличен от 0 => матрица невырожденная)
(отличен от 0 => матрица невырожденная)
Пусть матрица A
имеет размер
![]() (метод – разложение по первой строке)
(метод – разложение по первой строке)

 для матрицы
для матрицы
![]() - определитель 3-го порядка рассчитывается
через определители второго порядка
(определители 2 –го порядка рассчитываются
по формуле, приведённой выше)
- определитель 3-го порядка рассчитывается
через определители второго порядка
(определители 2 –го порядка рассчитываются
по формуле, приведённой выше)
Как запомнить формулу для определителя третьего порядка:
-
 умножается
на определитель матрицы
умножается
на определитель матрицы
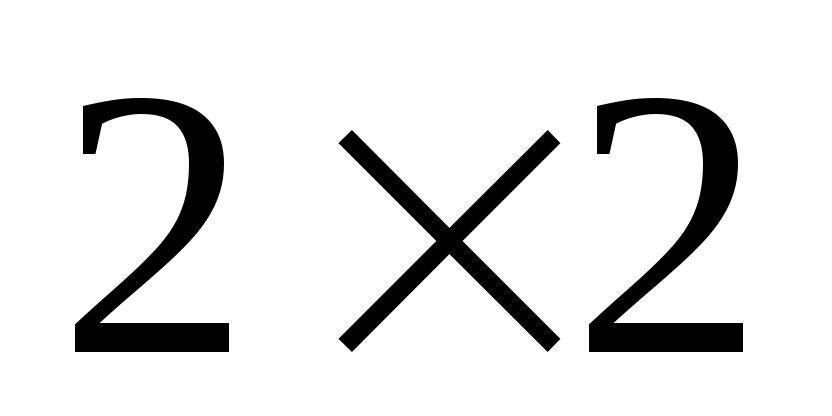 ,
которая получается из матрицы A
вычёркиванием строки и столбца с
,
которая получается из матрицы A
вычёркиванием строки и столбца с
 ,
,
-
 умножается на определитель матрицы
умножается на определитель матрицы ,
которая получается из матрицы A
вычёркиванием строки и столбца с
,
которая получается из матрицы A
вычёркиванием строки и столбца с
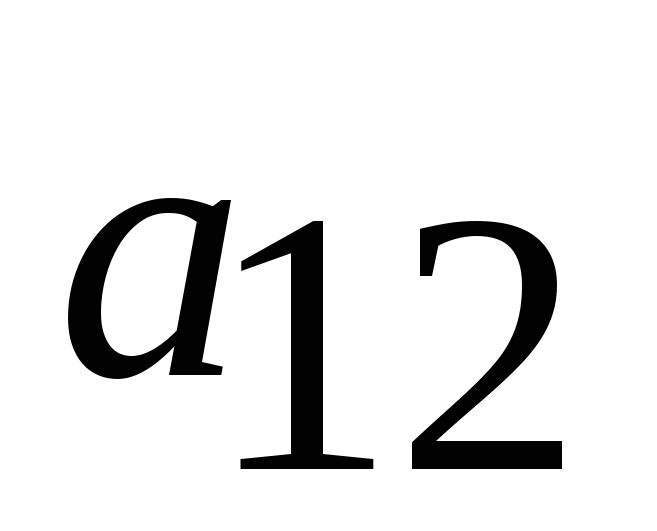 ,
,
-
 умножается на определитель матрицы
умножается на определитель матрицы
 ,
которая получается из матрицы A
вычёркиванием строки и столбца с
,
которая получается из матрицы A
вычёркиванием строки и столбца с
 ,
, -
Знаки в формуле чередуются «+», «-», «+»
Пример на вычисление определителя:

СЛОЖЕНИЕ МАТРИЦ (на
примере матриц
![]() )
)
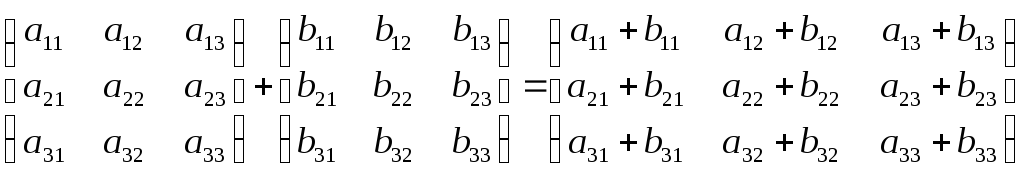
- матрицы складываются поэлементно (складываем числа на одинаковых
местах)
!!! Складывать можно только матрицы, имеющие одинаковый размер (т.е. одинаковое число строк и столбцов)
Пример:

Умножение матриц (
на примере матриц
![]() и
и
![]() )
)

или сокращённо
![]()
![]() формула для умножения матриц
формула для умножения матриц
![]() - матрицы A
и B
можно перемножать, если число столбцов
матрицы A
равно числу строк матрицы B.
Если матрица A имеет
размер
- матрицы A
и B
можно перемножать, если число столбцов
матрицы A
равно числу строк матрицы B.
Если матрица A имеет
размер
![]() ,
а матрица B имеет размер
,
а матрица B имеет размер
![]() ,
то матрица
,
то матрица
![]() имеет размер
имеет размер
![]() .
(
.
(![]() )
)
Пример:

(Матрица
![]() умножается на матрицу
умножается на матрицу
![]() . В результате получается матрица размера
. В результате получается матрица размера
![]() )
)
Получение первой строки матрицы C
![]() (
(![]() )
первую строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
)
первую строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
первую строку м-цы A
умножаем на второй столбец м-цы B
поэлементно и складываем
)
первую строку м-цы A
умножаем на второй столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
первую строку м-цы A
умножаем на третий столбец м-цы B
поэлементно и складываем
)
первую строку м-цы A
умножаем на третий столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
первую строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
)
первую строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
Получение второй строки матрицы C
![]() (
(![]() )
вторую строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
)
вторую строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
вторую строку м-цы A
умножаем на второй столбец м-цы B
поэлементно и складываем
)
вторую строку м-цы A
умножаем на второй столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
вторую строку м-цы A
умножаем на третий столбец м-цы B
поэлементно и складываем
)
вторую строку м-цы A
умножаем на третий столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
вторую строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
)
вторую строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
Получение третьей строки матрицы C
![]() (
(![]() )
третью строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
)
третью строку м-цы A
умножаем на первый столбец м-цы B
поэлементно и складываем
![]() (
(![]() )третью
строку м-цы A умножаем
на второй столбец м-цы B
поэлементно и складываем
)третью
строку м-цы A умножаем
на второй столбец м-цы B
поэлементно и складываем
![]() (
(![]() )третью
строку м-цы A умножаем на
третий столбец м-цы B
поэлементно и складываем
)третью
строку м-цы A умножаем на
третий столбец м-цы B
поэлементно и складываем
![]() (
(![]() )
третью строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
)
третью строку м-цы A
умножаем на четвертый столбец м-цы B
поэлементно и складываем
Умножение матрицы на число
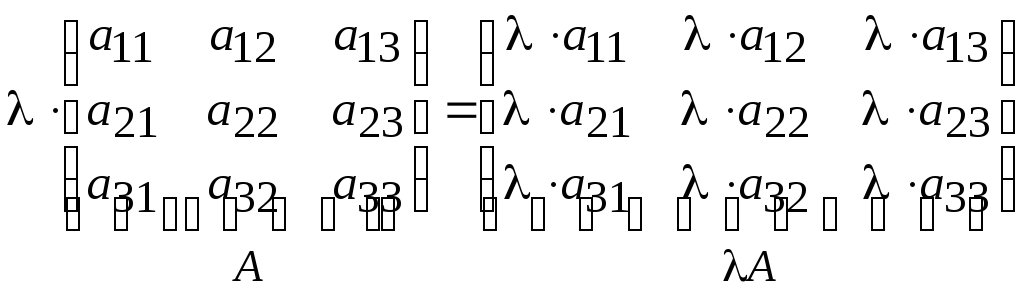
-при умножении матрицы на число каждый элемент матрицы умножается на число
ПРИМЕР:

Обратная матрица
Матрица
![]() называется обратной к матрице A,
если
называется обратной к матрице A,
если
![]() - в результате умножения получается
единичная матрица
- в результате умножения получается
единичная матрица
!!!
Обратная матрица
![]() существует, если
исходная матрица
существует, если
исходная матрица
![]() невырожденная, т.е.
невырожденная, т.е.
![]() .
Обратную матрицу можно определить
только для квадратных матриц.
.
Обратную матрицу можно определить
только для квадратных матриц.
Алгоритм поиска
обратной матрицы для матрицы
![]()
П усть
усть


