
- •Сборник задач по дисциплине
- •Содержание
- •1. Оценка эффективности реструктуризации фирмы Задача 1
- •2. Оценка риска и эффективности реализации проекта в условиях финансового оздоровления фирмы Задача 2
- •3. Прогнозирование дебиторской кризисустойчивости при коммерциализации разработок
- •Задача 3
- •Задача 4
- •4. Оценка кризисустойчивости фирмы на основеSwot-анализа
- •Задача 5
- •5. Расчет вероятности банкротства банков и фирм Задача 6
- •Задача 7
- •Задача 8
- •6. Многокритериальный метод прогнозирования кризисустойчивости предприятия
- •Задача 9
- •7. Инвестирование в условиях кризиса
- •Задача 10
- •Задача 11
- •Задача 12
- •Задача 13
- •8. Принятие управленческих решений в антикризисном менеджменте на основе статистических гипотез
- •Задача 14
- •Задача 15
- •Задача 16
- •Задача 17
- •Задача 18
- •Задача 19
- •9. Финансовый анализ и прогнозирование продаж в антикризисном управлении
- •Задача 20
- •Задача 21
- •Варианты заданий
- •10. Задачи анализа безубыточности и финансовой устойчивости предприятий
- •Задача 22
- •Задача 23
- •Задача 24
- •Варианты заданий
- •Задача 25
- •Задача 26
- •Задача 27
Задача 13
Распределение общей суммы инвестиций между проектами с разной прибыльностью с учетом их рискованности и дисконтирования.
Рассмотренная предыдущая задача предполагала по умолчанию выбор объема финансирования проектов без учета их индивидуальной рискованности, что принципиально нельзя игнорировать особенно для инновационных проектов.
Другой момент, который обязательно надо учитывать – это удешевление денег со временем, т.е. снижение реальной эффективности проектов со временем, при этом из-за различной рискованности проектов при расчете максимальной прибыльности за ряд лет может оказаться, что выбор объема финансирования проектов следует существенно корректировать.
Проиллюстрируем вышеизложенное на примере предыдущей задачи с теми же исходными данными.
Введем
коэффициент дисконтирования
![]() ,
который состоит из двух слагаемых
инфляционной
,
который состоит из двух слагаемых
инфляционной![]() и
и![]() -
коэффициент риска.
-
коэффициент риска.
![]()
Инфляционный
коэффициент
![]() прогнозируется государственными
органами и корректируется по итогам
года.
прогнозируется государственными
органами и корректируется по итогам
года.
Коэффициент
риск
![]() зависит от классификации инновационного
проекта, учитывающей около двух десятков
параметров [3], при этом
зависит от классификации инновационного
проекта, учитывающей около двух десятков
параметров [3], при этом![]() находится в пределах 0-30%.
находится в пределах 0-30%.
Известно, что дисконтированную доходность (W) проекта за ряд лет можно рассчитать по формуле:
![]() ,
,
где
![]() -
начальная доходность проекта,
-
начальная доходность проекта,![]() -
количество лет, за которые рассчитывается
доходность.
-
количество лет, за которые рассчитывается
доходность.
Для учета риска и дисконтирования в наших расчетах умножим доходность каждого j-го проекта по табл.3 по каждому объему инвестирования на коэффициенты:
За
1-й год:
![]()
![]() ;
;
За
2-й год:
![]() ;
;
За
3-й год:
![]() и т.д.
и т.д.
При
этом
![]() примем для наглядности результатов
анализа в следующих пределах:
примем для наглядности результатов
анализа в следующих пределах:
![]() и
и
![]() .
.
При
выборе конкретных значений
![]() принимался во внимание тот факт, что
чем более доходный проект, тем он более
рискованный.
принимался во внимание тот факт, что
чем более доходный проект, тем он более
рискованный.
С
учетом вышеизложенного целевая функция
прибыльности для нашего случая примет
вид:
![]() -
после 1-го года реализации; (Индекс 4 –
номер задачи)
-
после 1-го года реализации; (Индекс 4 –
номер задачи)
![]() -
после 2-го года реализации;
-
после 2-го года реализации;
![]() -
после 3-го года реализации;
-
после 3-го года реализации;
Проведя компьютерное моделирование в MS Excel, получим:
![]() =783 230
руб. (
=783 230
руб. (![]() =1)
=1)
При этом инвестиции по проектам распределяются в следующих суммах:
1 проект – 2 млн.руб.;
2 проект – 3 млн. руб.;
3 проект – 3 млн.руб.;
4 проект – 2 млн.руб.
Видно, что результат финансирования проектов отличается от рассмотренного в предыдущей задаче.
![]() =
1482170 руб. (
=
1482170 руб. (![]() =2)
=2)
Распределение финансирования:
1 проект – 2 млн.руб.;
2 проект – 4 млн. руб.;
3 проект – 2 млн.руб.;
4 проект – 2 млн.руб.
Опять
же, распределение финансирования по
проектам отличается от предыдущего
случая для
![]() =1.
=1.
![]() =2 056 000
руб. (
=2 056 000
руб. (![]() =3)
=3)
Распределение финансирования:
1 проект – 3 млн.руб.;
2 проект – 4 млн. руб.;
3 проект – 1 млн.руб.;
4 проект – 2 млн.руб.
Такое распределение отличается от всех предыдущих.
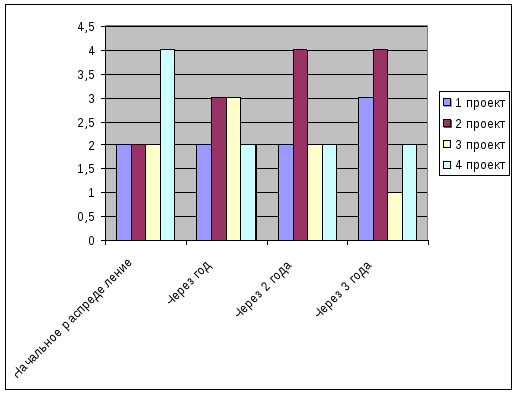
На
рис. представлена диаграмма распределения
финансирования по всем проектам для
случаев:
![]() =1,
=1,![]() =2,
=2,![]() =3
годам.
=3
годам.
Компьютерное моделирование инвестиционных задач инновационного менеджмента позволяет получать решения с широким набором практических условий, в том числе и задач динамического программирования.
При решении задач распределения средств между проектами с целью получения наибольшей прибыльности целесообразно учитывать риски проектов и обязательна привязка условия задачи к временному периоду, за который рассчитывается прибыль, т.к.эти факторы существенно сказываются на результатах анализа.
Список использованных источников
Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование : Учеб. пособие. – М.: Вузовский учебник, 2007. – 365с.
Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. 2-е изд. испр и доп. – Спб.:Издательство «Лань», 2005. – 528с. (Учебник для вузов. Специальная литература).
Финченко С.Н., Семиглазов В.А. Развитие метода дисконтного анализа эффективности инвестиционного проекта // Инновации. – 2008. – № 1. с. 108-111.
