Лабораторная работа №4

СМО с ожиданием

Одноканальная СМО с неограниченной очередью.

Задача 1

Булочная имеет одного контролера-кассира. В течение часа проходят в среднем 54 покупателя. Средняя стоимость 1 покупки составляет 15 руб. Среднее время обслуживания контролером-кассиром 1 покупателя составляет 4 мин. Определить выручку от продажи, основные характеристики СМО, дать оценку ее работы.

Решение.

По условиям задачи:

n = 1  = 54 ед/час  = 15 ед./час.

Интенсивность нагрузки:

 = / = 54/15 = 3,6

 > 1 – очередь с течением времени будет расти до бесконечности.

Q = р обс = 1

р отк = 0

Абсолютная пропускная способность:

не считается, она окажется > 

Выручка от продаж за 10 часов составит:

15 х 10 х 15 = 2250 руб.

Примечание: если в 1-канальной СМО с ожиданием интенсивность поступления заявок больше интенсивности обслуживания >, то очередь будет постоянно увеличиваться.

Поэтому наибольший интерес представляет анализ устойчивых СМО, работающих в стационарном режиме при <, < 1.

Скорректируем задачу:

Булочная имеет одного контролера-кассира. В течение часа проходят в среднем 24 покупателя. Средняя стоимость 1 покупки составляет 15 руб. Среднее время обслуживания контролером-кассиром 1 покупателя составляет 2 мин. Определить выручку от продажи, основные характеристики СМО, дать оценку ее работы.

Решение.

По условиям задачи:

n = 1  = 24 ед/час  = 30 ед./час.

Интенсивность нагрузки:

 = / = 24/30 = 0,8

 < 1 – очередь с течением времени не будет расти до бесконечности, следовательно, предельные вероятности существуют.

Вероятность того, что кассир свободен:

р₀ = 1 -  = 1- 0,8 = 0,2

Вероятность того, что кассир занят:

р_зан = 1 - р₀ = 1- 0,2 = 0,8

Среднее число покупателей в очереди:

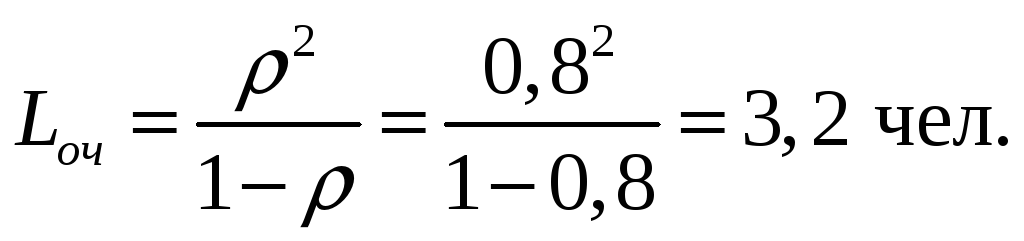
Среднее время ожидания в очереди:

Среднее время пребывания покупателей в булочной:

Т_СМО= Т_оч + t_обс = 8+2=10 мин.

Среднее число покупателей в булочной:

L_СМО = L_оч +  = 3,2 + 0,8 = 4 чел.

Q = р обс = 1

р отк = 0

Абсолютная пропускная способность:

A = Q* =  = 24 ед./час.

Следует уменьшить время обслуживания за счет введения дополнительного кассового аппарата.

Выручка от продаж за 10 часов:

24*10*15= 3600 руб.

Задача 2

Интенсивность потока автомобилей на АЗС к колонке за бензином АИ-92 составляет 30 автомобилей в час, а среднее время заправки равно 5 мин. Провести анализ работы СМО. Какое количество колонок должно работать, чтобы вероятность обслуживания составила 0,8.

Решение.

Одноканальная СМО с неограниченной очередью

По условиям задачи:

n = 1  = 30 ед/час  = 1/(1/12) ед./час.= 12 ед./час

Интенсивность нагрузки:

 = / = 30/12 = 2,5

 > 1 – очередь с течением времени будет расти до бесконечности. Режим работы нестационарный.

Q = р обс = 1

р отк = 0

Абсолютная пропускная способность:

А=  х Q = 30 ед/час

Среднее число обслуженных покупателей:

Lоб =  = 2,5 ед./час.

Необходимо ввести еще одну колонку или уменьшить время обслуживания до 1,5 мин. = 1/40 час.

При 2 колонках система превратится в многоканальную с отказами.

Вариант 2 – многоканальная СМО с отказами:

n	2	3	4
p0	0,151	0,108	0,028
ps	0,528	0,718	0,954
pr	0,472	0,282	0,046

простой

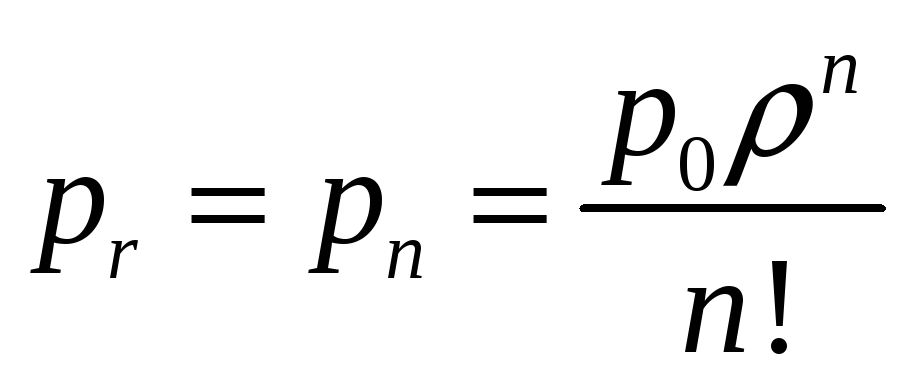отказ

обслуживание

Домашнее задание:

Задача 1

Порт имеет один грузовой причал для разгрузки судов. Интенсивность потока судов составляет 0,5 судов/сутки. Среднее время разгрузки одного судна – 2 суток. Если в очереди на разгрузку стоят 3 судна, то вновь прибывшее судно покинет причал неразгруженным. Найти показатели эффективности работы причала.

Задача 2

На станцию технического обслуживания поступает простейший поток заявок с интенсивностью 1 автомобиль за 2 часа. Среднее время ремонта – 1,5 часа. Провести анализ работы СМО.

Решение.

По условиям задачи:

n = 1  = 0,5 ед/час  = 0,67 ед./час.

Интенсивность нагрузки:

 = / = 0,5/0,67 = 0,75

 < 1 – очередь с течением времени не будет расти до бесконечности, следовательно, предельные вероятности существуют.

Вероятность того, что станция свободна:

р₀ = 1 -  = 1- 0,75 = 0,25

Вероятность того, что станция занята:

р_зан = 1 - р₀ = 1- 0,2 = 0,75

Среднее число машин в очереди:

Среднее время ожидания в очереди:

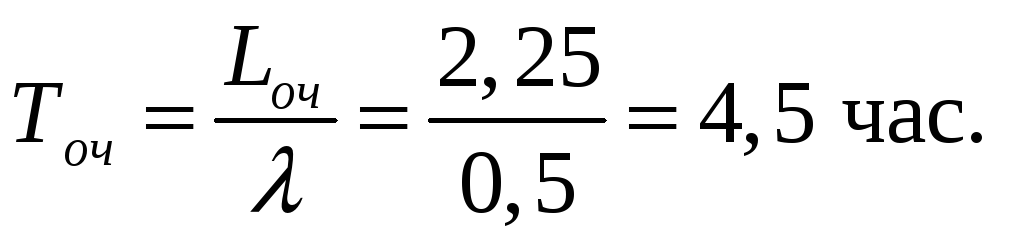
Среднее время пребывания машин на станции:

Т_СМО= Т_оч + t_обс = 4,5+1,5= 6 час.

Среднее число машин в мастерской:

L_СМО = L_оч +  = 2,25 + 0,75 = 3 маш.

Следует ускорить ремонт 1 машины, или завести еще 1 бокс для ремонта.

Одноканальная СМО с ограниченной очередью.

Задача 1

На автомойку в среднем за час приезжают 3 автомобиля, если в очереди уже находятся 2 автомобиля, то вновь прибывшие автомобили покидают мойку. Среднее время мойки 1 автомобиля – 20 мин. Мест для мойки – 1. Проанализировать работу мойки за 12 часов. Средняя стоимость мойки 1 автомобиля – 70 руб.

Решение:

одноканальная СМО с ограничениями по очереди.

n=1 m=2

Интенсивность потока заявок

λ = 3

Интенсивность обслуживания заявок

μ = 1/t_обс =1/0,33 = 3

время обслуживания 1 заявки

t_обс = 20/60 = 0,33 час.

Интенсивность нагрузки:

 = * t_обс = 3* 0,33 = 1

Вероятности состояний СМО равны поскольку  = 1

р₀ = р₁ = р₂ = р₃ = 1/m+2 = 1/4 = 0,25

Относительная пропускная способность

Q = 1- 0,25 = 0,75

Абсолютная пропускная способность:

А = Q * λ = 0,75*3 = 2,25

Средняя длина очереди:

L_оч = m*(m+1)/2*(m+2)

L_оч = 2*(2+1)/2*(2+2) = 0,75

Среднее время ожидания в очереди:

Т_оч = L_оч/А = 0,75 / 2,25 = 0,33 час.

Среднее число заявок в очереди:

L_СМО =( m+1)/2 = 3/2 = 1,5

Среднее время пребывания машины на мойке:

Тсмо = (m+1)/2* μ = 3/(2*3) = 0,5 час.

Многоканальная СМО с неограниченной очередью.

Задача 1

В магазине самообслуживания установлены два кассовых аппарата. Интенсивность входного потока в будние дни в среднем составляет 1,3 покупателя/мин. до обеда, 1,8 покупателя/мин – после обеда, а в субботу и воскресенье – в среднем 2,2 покупателя /мин. Среднее время обслуживания покупателя контролером-кассиром составляет 52с. Провести анализ работы СМО.

Решение.

1. Определим характеристики СМО для каждого варианта.

Среднее число занятых каналов

 = ₁х t_обс = 1,3*52/60 = 1,13

n = 2

<n возможен стационарный режим работы

Нагрузка на 1 канал – коэффициент занятости каналов:

Ψ1 = ρ1/n = 1,13/2 = 0,56

Ψ2 = 1,56/2 = 0,78

Ψ3 = 1,91/2 = 0,95

2. Доля времени простоя кассиров:

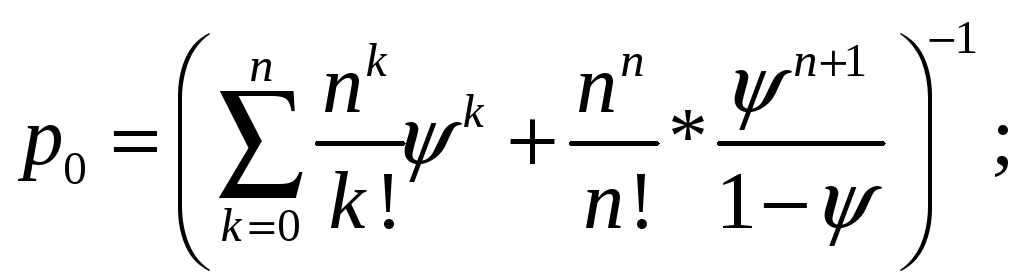
р₀1 = 0,28

р₀2 = 0,12

р₀3 = 0,024

3. Вероятность оказаться в очереди:

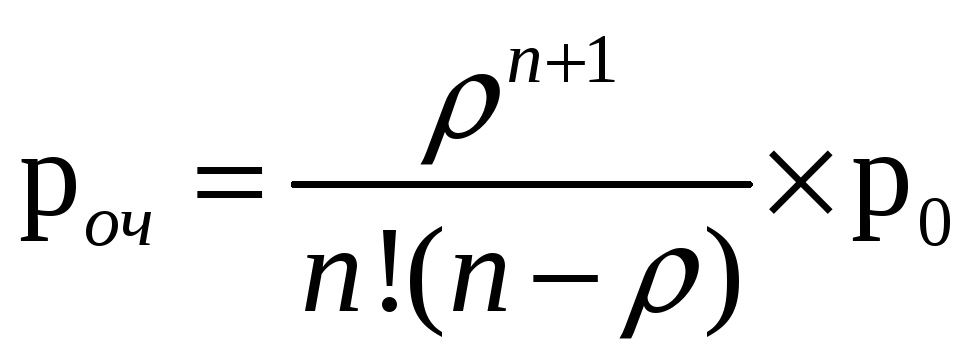
р_оч1= 0,23

р_оч2= 0,53

р_оч3= 0,89

4. Среднее число покупателей в очереди:

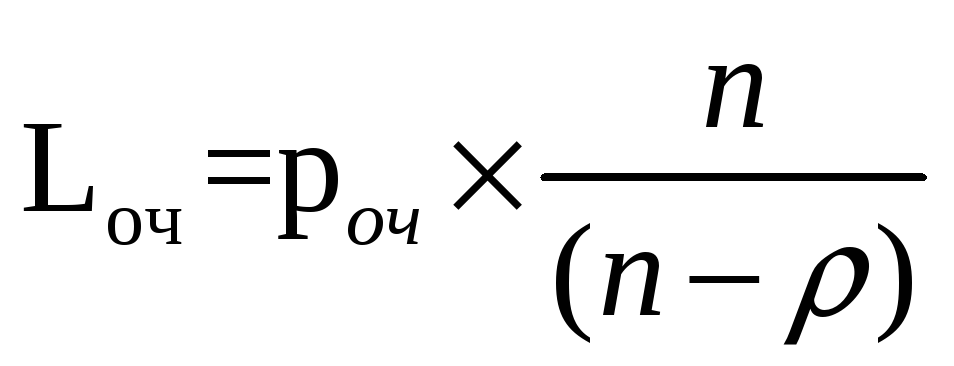
L_оч1 = 0,52

L_оч2 = 2,4

L_оч3= 19

5. Среднее число занятых каналов:

L_СМО = L_оч + 

L_СМО1 = 1,65

L_СМО2 = 3,98

L_СМО3 = 20,9

6. Среднее время пребывания покупателя в очереди:

Точ = L_оч/

Точ1 = 0,4

Точ2 = 1,35

Точ3 = 8,64

7. Среднее время пребывания покупателя в магазине:

Т_СМО = Т_оч + t_обс

Т_СМО1 =0,4 + 52/60 = 1,27

Т_СМО2 = 2,21

Т_СМО3 = 9,51 мин.

Вывод:

Интенсивность входного потока влияет на все характеристики СМО. Доля времени простоя уменьшается до 2,5%, вероятность образования очереди увеличивается до 89%. Среднее число покупателей в очереди в выходные дни составляет 19 человек, что недопустимо. Через некоторое время последует потеря вероятностных клиентов. Следует вводить еще 1 кассовый аппарат в выходные дни.

Задача 2

В магазине самообслуживания 6 кассиров. Входящий поток покупателей подчиняется закону Пуассона с интенсивностью 120 чел./ч. Один кассир может обслужить 40 человек в час. Определить вероятность, долю времени простоя кассира, среднее число занятых кассиров. Дать оценку работы СМО.

Решение.

Многоканальная СМО с неограниченной очередью

n = 6  = 120  = 40

1. Определим характеристики СМО.

Среднее число занятых каналов

 = / = 120/40 = 3

<n возможен стационарный режим работы

Нагрузка на 1 канал – коэффициент занятости каналов:

Ψ = ρ/n = 3/6 = 0,5

2. Доля времени простоя кассиров:

р₀ = ((1+6*0,5+6^2/2*0,5^2+6^3/3!*0,5^3 + 6^4/4!*0,5^4+ 6^5/5!*0,5^5 +6^6/6!*0,5^6 ) + 6^6/6!*0,5^7/(1-0,5))^(-1) = 0,049

3. Вероятность оказаться в очереди:

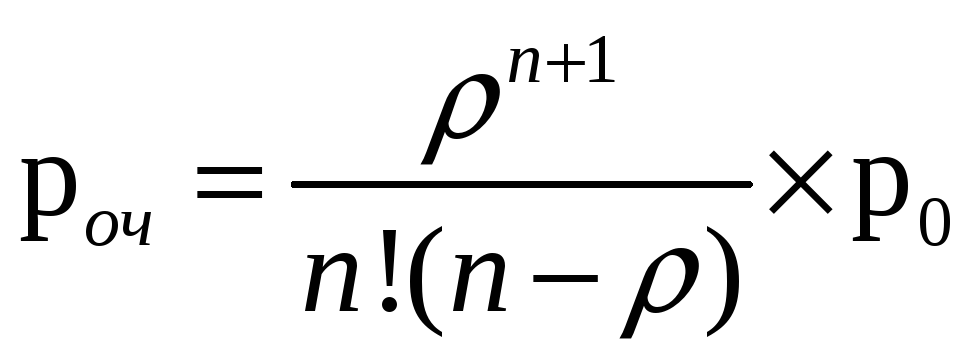
р_оч= 3^7/(6!*(6-3))*0,049 = 0,05

4. Среднее число покупателей в очереди:

L_оч = 0,05*6/(6-3) = 0,1 чел.

5. Среднее число занятых каналов:

L_СМО = L_оч +  = 0,1 + 3 = 3,1

6. Среднее время пребывания покупателя в очереди:

Точ = L_оч/ = 0,1/120 = 0,0008 час.

7. Среднее время пребывания покупателя в магазине:

Т_СМО = Т_оч + t_обс = 0,0008 + 1/40 = 0,0258час.

Домашнее задание

Задача 1

На таможне имеется 3 терминала. Интенсивность потока машин, перевозящих грузы и подлежащих прохождению таможенного контроля, составляет 30 машин в сутки. Среднее время таможенного досмотра 1 машины составляет 3 часа. Если в очереди на прохождение контроля стоят уже 5 машин, вновь прибывшие машины получают отказ. Найти показатели эффективности работы таможни.

Задача 2

В расчетном узле магазина самообслуживания работают три кассы. Интенсивность входного потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждого контроллера-кассира составляет 2 покупателя в минуту. Определить основные характеристики СМО. Дать оценку ее работы.

Задача 3

В справочную поступают телефонные запросы с интенсивностью 80 заявок в час. Оператор справочной обрабатывает запрос в течение 0,7 мин. Если оператор занят, то заявка ставится в очередь. Длина очереди не должна превышать 4 заявок. Дать оценку работы справочной и вариант ее реорганизации.

8