14. Способы преобразования проекций. Способ плоскопараллельного перемещения.

Способы преобразования проекций: перемена плоскостей проекций; вращение вокруг проецирующей прямой; вращение вокруг линий уровня; плоскопараллельное перемещение; совмещение.Задачи: а) прямая общего положения преобразуется в прямую уровня; б) прямая уровня преобразуется в проецирующую прямую; в) плоскость общего положения преобразуется в проецирующую плоскость; г) проецирующая плоскость преобразуется в плоскость уровня.

Способ плоскопараллельного перемещения.

Сущность этого способа заключается в перемещении геометрической фигуры относительно данных плоскостей проекций в частное положение таким образом, чтобы траектория перемещения всех ее точек находилась в параллельных плоскостях. Плоскопараллельное перемещение — общий случай вращения без указания местоположения оси. При параллельным переносе геометрической фигуры относительно плоскостей проекций проекция фигуры на эту плоскость хоть и изменяет свое положение, но не изменяется по форме и размерах.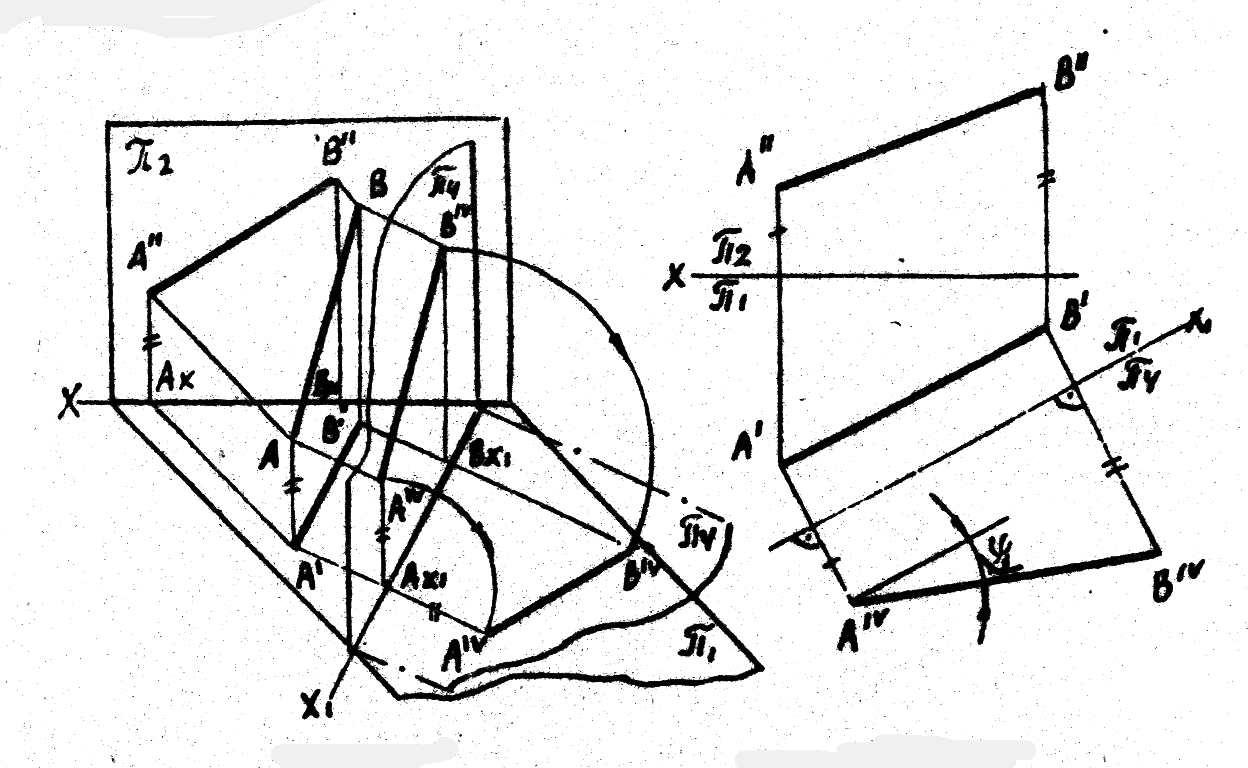

15. Способ замены плоскостей.

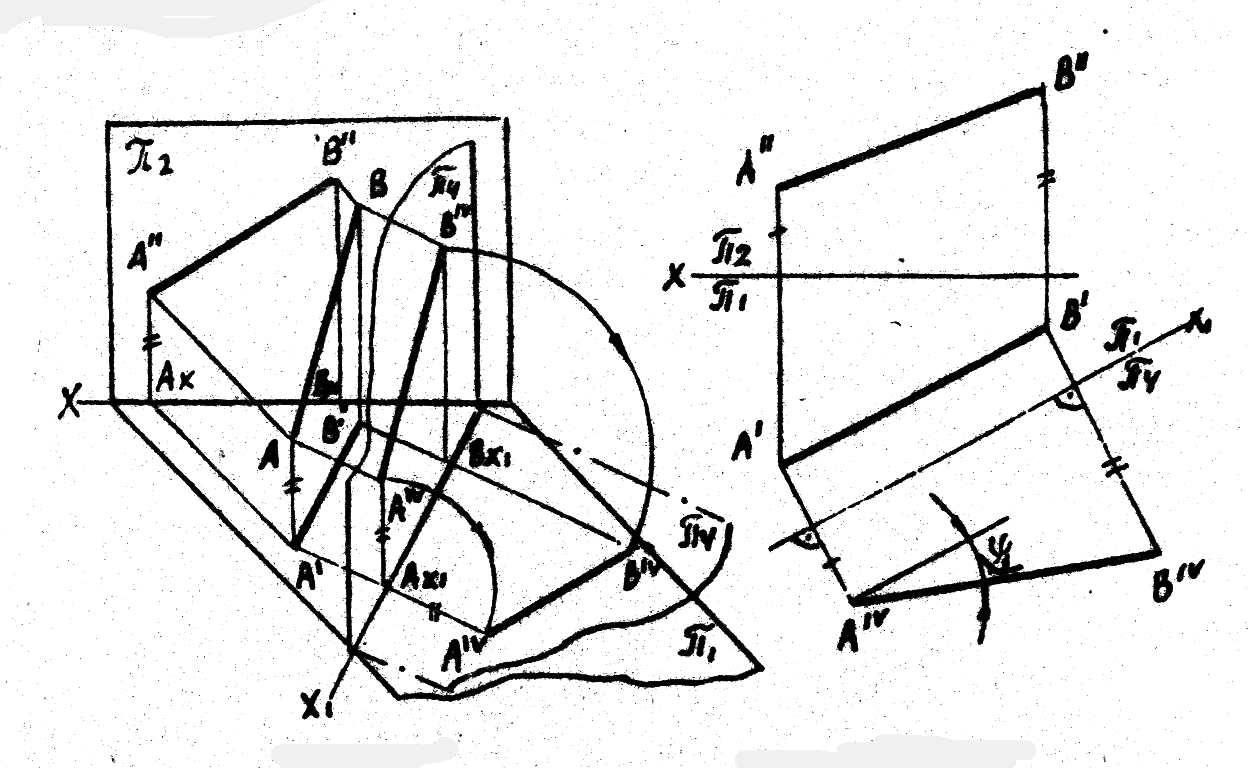
Сущность этого способа заключается в переходе от данной системы плоскостей проекций П₁/П₂к новой. Проецируемая фигура при этом не меняет своего положения в пространстве. Одна из основных плоскостей проекций П₁или П₂заменяется новой плоскостью, размещенной определенным образом относительно неподвижного объекта проецирования. Поскольку в новой системе плоскостей проекций проецирование остается прямоугольным, то новая плоскость должна быть перпендикулярной к незамененной плоскости проекций П₁или П₂.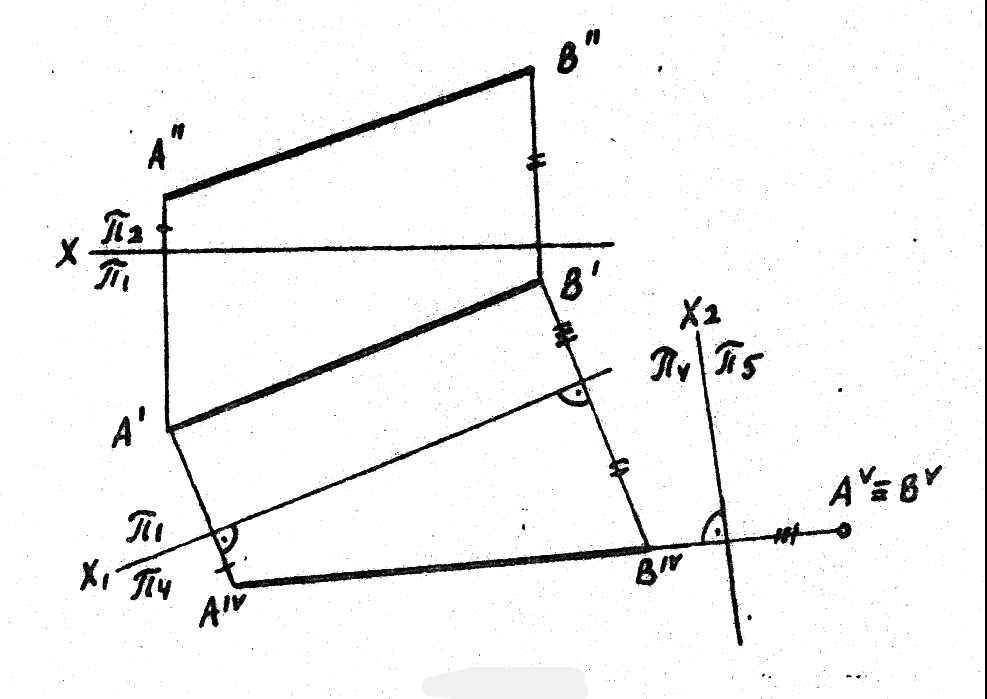

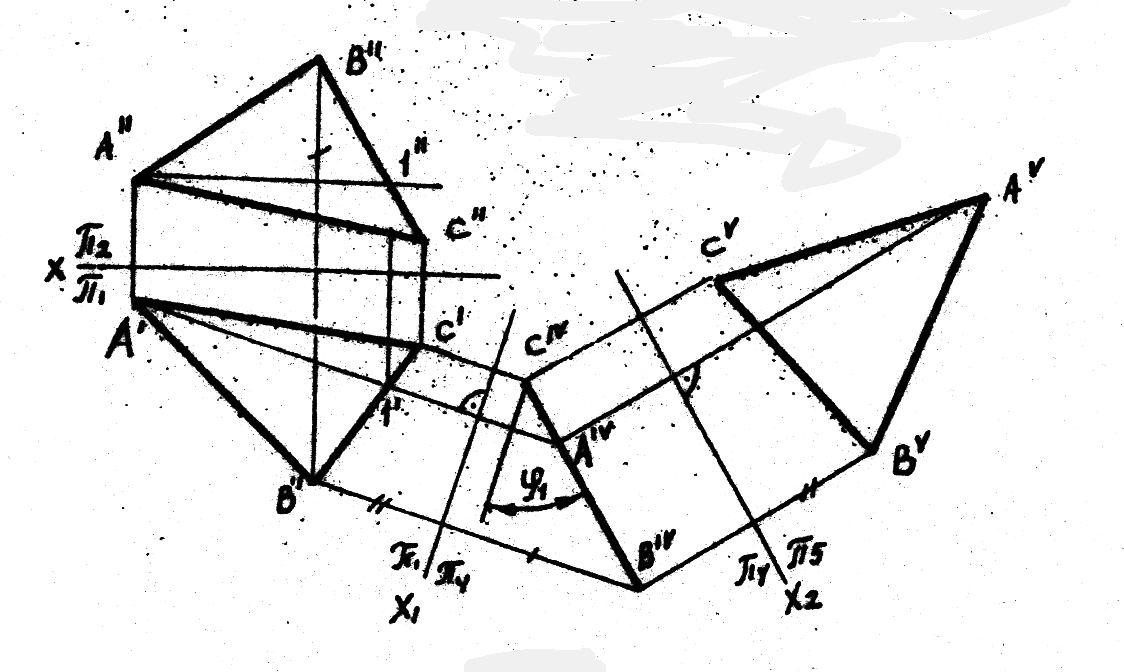
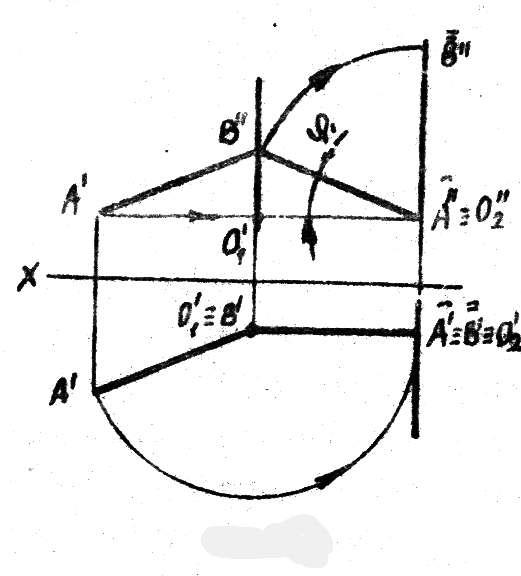
16. Способ вращения вокруг проецирующих прямых.

Сущность способа заключается в том, что данная система плоскостей проекций остается неизменной, а проецируемую фигуру вращают вокруг неподвижной оси, перпендикулярной к одной из плоскостей проекций, до той пары, пока она не займет частное положение, т.е. при вращении плоскость сохраняет свое первоначальное положение, а геометрический образ перемещается в пространстве. Центр вращения — точка пересечения оси вращения с плоскостью вращения. Радиус вращения — расстояние от центра вращения до заданной точки.

17. Пересечение многогранников плоскостью частного положения.

Cечение — изображение фигуры, полученной в секущей плоскости. Способ ребер подразумевает определение точек пересечение ребер с заданной плоскостью. Способ граней определяет линии пересечения граней многогранника с заданной плоскостью.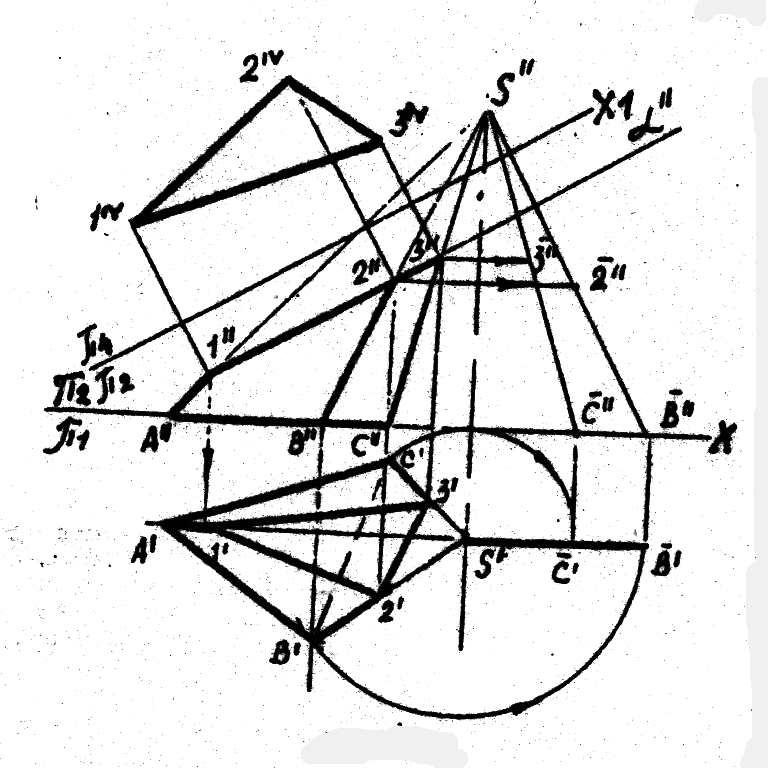

18. Развертки поверхностей. Развертывание поверхности многогранников.

Развертка — плоская фигура, получающаяся при совмещении поверхности с плоскостью. При совмещении всех граней многогранника с плоскостью в такой последовательности, в которой они размещены в многограннике, получается развертка его поверхности. Для построения развертки нужно найти натуральную величину всех граней многогранника и фигуры сечения. Три вида разверток: точные (призмы, пирамиды); приближенные (поверхности вращения заменяют многогранной поверхностью); условные (поверхности заменяются абсолютно другой).