21. Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок.

 Классическая линейная модель множественной регрессии (КЛММР)

Классическая линейная модель множественной регрессии (КЛММР) представляет собой простейшую версию конкретизации требований к общему виду функции регрессии f(X), природе объясняющих переменных X и статистических регрессионных остатков (Х) в общих уравнениях регрессионной связи (2.3)^[1]. В рамках КЛММР эти требования формулируются следующим образом:

Из (2.5) следует, что в рамках КЛММР рассматриваются только линейные функции регрессии, т.е.

где объясняющие переменные x⁽¹⁾, x⁽²⁾,…, x^(p) играют роль неслучайных параметров, от которых зависит закон распределения вероятностей результирующей переменной y. Это, в частности, означает, что в повторяющихся выборочных наблюдениях (x_i⁽¹⁾, x_i⁽²⁾,..., х_i^(p); y_i) единственным источником случайных возмущений значений y_i являются случайные возмущения регрессионных остатков _i (подобную схему зависимости мы наблюдали в примере 10.1 из тома 1).

Кроме того, постулируется взаимная некоррелированность случайных регрессионных остатков (E(_i_j) = 0 для i  j). Это требование к регрессионным остаткам ₁,...,_n относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций, особенно, если речь идет о пространственных выборках (2.4^а)-(2.4^б), т.е. о ситуациях, когда значения анализируемых переменных регистрируются на различных объектах (индивидуумах, семьях, предприятиях, банках, регионах и т. п.). В этом случае данное предположение означает, что «возмущения» (регрессионные остатки), получающиеся при наблюдении одного какого-либо обследуемого объекта, не влияют на «возмущения», характеризующие наблюдения над другими объектами, и наоборот.

Тот факт, что для всех остатков ₁,₂,...,_n выполняется соотношение E_i²; =² , где величина ² от номера наблюдения i не зависит, означает неизменность (постоянство, независимость от того, при каких значениях объясняющих переменных производятся наблюдения) дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков.

Наконец, требуется, чтобы ранг матрицы X, составленной из наблюденных значений объясняющих переменных, был бы максимальным, т. е. равнялся бы числу столбцов этой матрицы, которое в свою очередь должно быть меньше числа ее строк (т. е. общего числа имеющихся наблюдений). Случаи р + 1  n не рассматриваются, поскольку при этом число п имеющихся в нашем распоряжении исходных статистических данных оказывается меньшим или равным числу оцениваемых параметров модели (р + 1), что исключает принципиальную возможность получения сколько-нибудь надежных статистических выводов. Что касается требования к рангу матрицы X, то оно означает, что не должно существовать строгой линейной зависимости между объясняющими переменными. Так, если, например, одна объясняющая переменная может быть линейно выражена через какое-то количество других, то ранг матрицы X окажется меньше р + 1, а следовательно, и ранг матрицы X^TX будет тоже меньше р + 1 (см. Приложение 2). А это означает вырождение симметрической матрицы Х^TХ (т.е. det(X^TX) = 0), что исключает существование матрицы (X^TX)^-1 , которая, как мы увидим, играет важную роль в процедуре оценивания параметров анализируемой модели.

В дальнейшем нам удобнее будет оперировать с матричной записью модели (2.5). При этом кроме обозначений (2.4^а)-(2.4^б) введем также матрицы (векторы):

единичная матрица размерности п х п;

вектор-столбец неизвестных значений параметров;

вектор-столбец регрессионных остатков;

вектор-столбец высоты п, состоящий из одних нулей;

ковариационная матрица размерности п х п вектора остатков;

вектор-столбец оценок неизвестных значений параметров;

ковариационная матрица размерности (р+1)*(р+1) вектора несмещенных оценок  неизвестных параметров  (в соотношении (2.13) _lj() = Е[(_l -_l)(_j -_j ))

Тогда матричная форма записи КЛММР имеет вид:

(2.5`)

Когда дополнительно к условиям (2.5) (или (2.5`)) постулируют нормальный характер распределения регрессионных остатков  = (₁,₂,..., _n)^T(что записывается в виде   N_n (0; ² I_n)), то говорят, что у и X связаны нормальной КЛММР.

Коренное отличие обобщенной модели от классической состоит только в виде ковариационной квадратной матрицы вектора возмущений: вместо матрицы Σ_ε = σ²E_n для классической модели имеем матрицу Σ_ε = Ω для обобщенной. Последняя имеет произвольные значения ковариаций и дисперсий. Например, ковариационные матрицы классической и обобщенной моделей для двух наблюдений (п=2) в общем случае будут иметь вид: Формально обобщенная линейная модель множественной регрессии (ОЛММР) в матричной форме имеет вид: Y = Xβ + ε                                                 (1) и описывается системой условий: 1.     ε – случайный вектор возмущений с размерностью n; X -неслучайная матрица значений объясняющих переменных (матрица плана) с размерностью nх(р+1); напомним, что 1-й столбец этой матрицы состоит из пединиц; 2.     M(ε) = 0_n – математическое ожидание вектора возмущений равно ноль-вектору; 3.     Σ_ε = M(εε’) = Ω, где Ω – положительно определенная квадратная матрица; заметим, что произведение векторов ε‘ε дает скаляр, а произведение векторов εε’ дает матрицу размерностью nxn; 4.     Ранг матрицы X равен р+1, который меньше n; напомним, что р+1 - число объясняющих переменных в модели (вместе с фиктивной переменной), n - число наблюдений за результирующей и объясняющими переменными. Следствие 1. Оценка параметров модели (1) обычным МНК b = (X’X)^-1X’Y                                                (2) является несмещенной и состоятельной, но неэффективной (неоптимальной в смысле теоремы Гаусса-Маркова). Для получения эффективной оценки нужно использовать обобщенный метод наименьших квадратов. Следствие 2. Для классической модели ковариационная матрица вектора оценок параметров определялась формулой: Σ_b = σ²(X’X)^-1                                                         (3) Эта оценка для обобщенной модели является смещенной (следовательно, и неэффективной).  Следствие 3. Для обобщенной модели ковариационная матрица вектора оценок параметров определяется другой формулой: Σ _b* = (X’X)^-1X’ΩX(X’X)^-1                                         (4)

При оценке параметров уравнения регрессии мы применяем метод наименьших квадратов (МНК). В модели у =  + ₁х + ₂ р + е, случайная составляющая (е) представляет собой «необъясненную или ненаблюдаемую величину». После того, как произведено решение модели, то есть дана оценка параметрам, мы можем определить величину остатков в каждом конкретном случае как разность между фактическими и теоретическими значениями результативного признака е_i=y_i-. Поскольку это не есть реальные остатки, то мы их считаем лишь выборочной реализацией неизвестного остатка заданного уравнения. При изменении спецификации модели, добавления в нее новых наблюдений, выборочные оценки остатков могут меняться, поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений, то есть остаточных величин.

В предыдущих разделах мы останавливались на формально-математических проверках статистической достоверности коэффициентов регрессии и корреляции с помощью Т-критерия Стьюдента и критерия Фишера. При использовании этих критериев делаются предположения относительно поведения остатков: предполагают, что 1) остатки представляют собой независимые случайные величины и их среднее значение равно нулю; 2) остатки имеют постоянную дисперсию и подчиняются закону нормального распределения.

Пока мы не построим модель, остатки определены быть не могут, и поэтому мы не можем проверить, обладают ли они этими свойствами или нет. Таким образом, проверяя статистическую достоверность параметров связи, мы опираемся всего лишь на непроверенные предпосылки о распределении случайной составляющей уравнения регрессии. Но после построения уравнения регрессии мы уже можем определить остатки и проверить у них наличие тех свойств, которые предполагались вначале.

С чем связана необходимость проверки таких свойств? Связано это с тем, что выборочные оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют важное практическое значение в использование результатов регрессии и корреляции.

Несмещенные оценки означают, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оценок коэффициента регрессии в найденный параметр по результатам одной выборки можно рассматривать как среднее значение из большого числа несмещенных оценок.

Оценки считаются эффективными, если они характеризуются меньшей дисперсией (то есть мы имеем минимальную вариацию выборочных оценок).

Оценки считаются состоятельными, если их точность увеличивается с увеличением объема выборки.

Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Предпосылки МНК:

1. случайный характер остатков;

2. гомоскедастичность – дисперсия остатков одинакова для всех значений фактора;

3. отсутствие автокорреляции остатков (то есть остатки распределены независимо друг от друга);

4. остатки подчиняются нормальному закону распределения.

В тех случаях, когда эти предпосылки выполняются, оценки, полученные по МНК, будут обладать вышеназванными свойствами, если же некоторые предпосылки не выполняются, то необходимо корректировать модель.

Итак, проверяем случайный характер остатков. С этой целью строится график зависимости остатков от теоретических значений результативного признака (рис.5.2.1.)

Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и МНК оправдан.

Возможны иные случаи (рис.5.2.2):

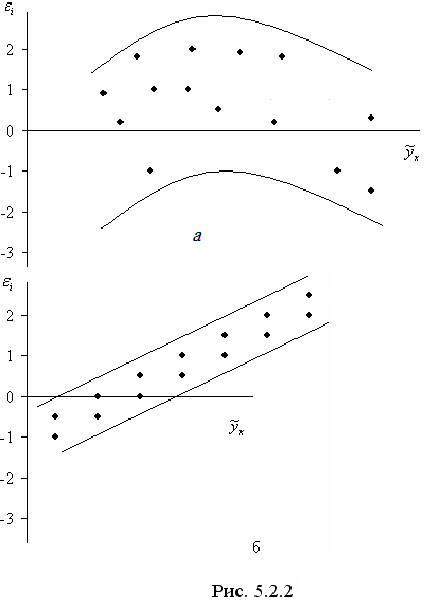
а) – остатки носят систематический характер, то есть отрицательные значения соответствуют низким значениям расчетных «у», а положительные – высоким;

б) – преобладание положительных остатков над отрицательными. В этих случаях необходимо применять либо другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.

Вторая предпосылка МНК требует, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора остатки имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гомо- или гетероскедастичности можно видеть по графику зависимости остатков от теоретических значений результативного признака (рис. 5.2.3.):

а) большая дисперсия остатков для больших значений «у» (гетероскедастичность);

б) большая дисперсия остатков для средних значений «у» (гетероскедастичность);

в) – большая дисперсия для меньших значений результата (гетероскедастичность);

г) – равная дисперсия (гомоскедастичность).

Наличие гетероскедастичности приводит к смещенным оценкам коэффициентов регрессии, а также уменьшает их эффективность. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии, которая предполагает единую дисперсию остатков.

Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- или гетероскедастичности. Однако, чтобы убедиться в наличии этих качеств, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят также ее количественное подтверждение. При малом объеме выборки, что характерно для эконометрических исследований для этих целей используется метод Гольдфельда –Квандта, который включает в себя следующие шаги:

1. Упорядочение наблюдений по мере возрастания фактора х.

2. Исключение из наблюдений нескольких центральных наблюдений (С). При этом должно выполняться условие, что (N – С)/2 должно быть больше р – число параметров в модели.

3. Распределение оставшихся наблюдений на две равные группы с малыми и большими значениями факторного признака.

4. Решение уравнения регрессии для каждой группы (имеем два уравнения).

5. Определение остаточной суммы квадратов отклонений для каждой группы и определение их отношения (отношение большей к меньшей).

6. Сравнение этого отношения с табличным значением критерия Фишера (d f = n - C – 2p/2). Если это отношение меньше табличного значения F- критерия, то мы имеем гомоскедастичные остатки. Чем больше это отношение превышает табличное, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.

Следующая предпосылка МНК – это отсутствие автокорреляции остатков. Это означает, что остатки распределены независимо друг от друга. Автокорреляция – это наличие тесной корреляционной зависимости между остатками текущих и предшествующих наблюдений, если наблюдения упорядочены по фактору х. Автокорреляционная зависимость определяется по линейному коэффициенту корреляции между текущими и предшествующими наблюдениями (более подробно с этой проблемой мы ознакомимся в теме «Моделирование рядов динамики»). Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

Соответствие распределение остатков нормальному закону распределения можно проверить с помощью критерия Пирсона как критерия согласия (изучалось в курсе «Математическая статистика»).

При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять или исключать некоторые факторы, преобразовывать исходные данные. В частности, при нарушении гомоскедастичности и наличии автокорреляции остатков рекомендуется традиционный МНК, который проводится по исходным данным, заменять обобщенным методом наименьших квадратов, который проводится по преобразованным данным.

22. Прогноз и оценка точности МНК на основе уравнений парной и множественной линейной регрессии

Метод наименьших квадратов (МНК, OLS, Ordinary Least Squares) — один из базовых методов регрессионного анализадля оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.

Сущность МНК

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

где — вектор неизвестных параметров модели

 — случайная ошибка модели.

Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть — номер наблюдения (). Тогда— значения переменных в-м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:

Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков (англ.Residual Sum of Squares^[1]) будет минимальной:

где:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ.Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:

Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценкамиметода максимального правдоподобия (ММП).

МНК в случае линейной модели

Пусть регрессионная зависимость является линейной:

Пусть y — вектор-столбец наблюдений объясняемой переменной, а — это-матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях).Матричное представлениелинейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):

.

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

 где все суммы берутся по всем допустимым значениям .

Если в модель включена константа (как обычно), то при всех, поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений, а в остальных элементах первой строки и первого столбца — просто суммы значений переменных:и первый элемент правой части системы —.

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итогестандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.

[править]Простейшие частные случаи

В случае парной линейной регрессии , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

Отсюда несложно найти оценки коэффициентов:

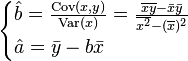
Несмотря на то что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели. В этом случае вместо системы уравнений имеем единственное уравнение

Следовательно, формула оценки единственного коэффициента имеет вид

Свойства МНК-оценок

В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенностиМНК-оценок необходимо и достаточно выполнения важнейшего условиярегрессионного анализа: условное по факторамматематическое ожиданиеслучайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если

1. математическое ожидание случайных ошибок равно нулю, и

2. факторы и случайные ошибки — независимые случайные величины.

Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Второе условие — условие экзогенностифакторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут дажесостоятельными(то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицык некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

• Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности):

• Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой

Данные предположения можно сформулировать для ковариационной матрицывектора случайных ошибок

Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными,состоятельнымии наиболееэффективнымиоценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуруBLUE(Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

Эффективностьозначает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещённымиисостоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективнымиоценками (оставаясьнесмещённымиисостоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становитсясмещённойинесостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайтаистандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемогообобщённого МНК.

Обобщенный МНК

Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную формуот вектора остатков, где— некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение. Следовательно, указанный функционал можно представить следующим образом, то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

Ковариационная матрица этих оценок соответственно будет равна

Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

Взвешенный МНК

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.