1.3 Показатели вариации

1.3.1 Размах вариации

Вариация ( изменчивость, колеблемость) значений признака- это характерная особенность любой статистической совокупности. Для ее измерения используется система показателей, включающая в себя абсолютные , средние и относительные величины. Наиболее простым с точки зрения расчета является такой абсолютный показатель вариации как размах вариации : R = . Он отражает максимальную изменчивость признака. Достоинство простоты расчета оборачивается таким существенным недостатком как опора только на два, тем более крайних в ранжированном ряду значения.

1.3.2 Среднее линейное отклонение

Для того, чтобы учесть изменчивость всех без исключения значений можно сравнить каждое значение с каждым, но в этом случае из-за равенства суммы отклонений 0 ( нулю ) не –возможно выйти на некий единый показатель. Учесть в едином показателе изменчивость всех без исключения значений можно путем сравнения каждого значения с постоянной величиной, взявв качестве таковой среднюю арифметическую ( гармоническую ).Однако , сумма этих отклонений также равна 0, что делает на первый взгляд расчет единого показателя вариации. Если же каждое отклонение взять по абсолютной величине ( по модулю ) , то

можно получить следующий абсолютный показатель вариации –

сумму линейных отклонений взятых по модулю , а на основе этого показателя среднее линейное отклонение :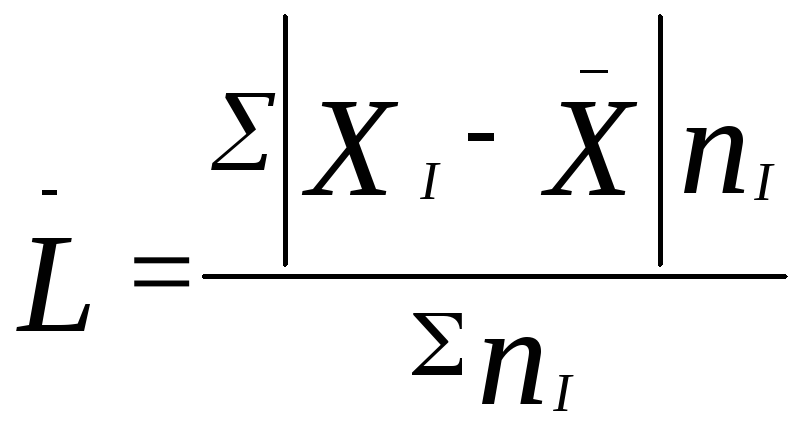. Данный показатель говорит о том насколько в среднем каждое значение признака по абсолютной величине отличается от средней арифметической ( гармонической ). Этот показатель представляет собой типичный размер отклонений лишь в том случае, если число отрицательных и положительных отклонений примерно одинаково, то есть распределение симметрично или близко к нему. В противном случае следует отдельно рассчитать среднее из отрицательных и среднее из положительных отклонений.

1.3.3 Объем вариации, дисперсия, стандартное отклонение

Уйти от 0 (ноля) при суммировании отклонений каждого

значения от средней можно также путем предварительного возведения отклонений в квадрат. В этом случае мы получим еще один абсолютный показатель вариации: объем вариации или сумму квадратов отклонений W = (, на основе которого может быть рассчитан объем вариации , приходящийся на единицу наблюдения ( дисперсия или средний квадрат отклонений ) :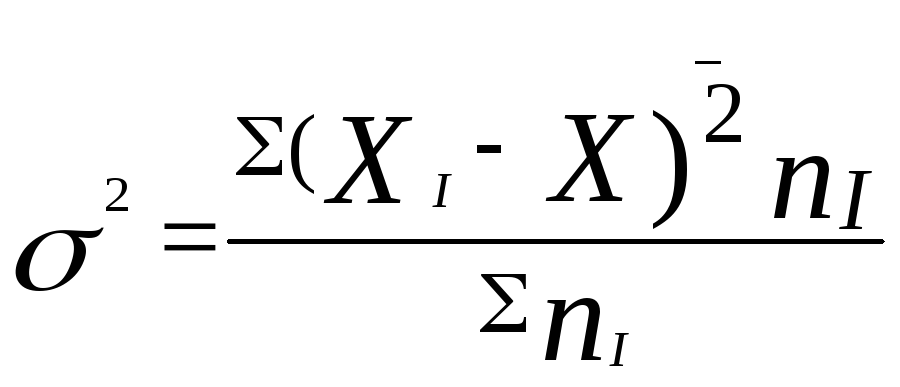. Извлекая корень квадратный из дисперсии получим типичный размер отклонений каждого значения признака от средней, а именно стандартное или среднее квадратическое отклонение ().которое показывает насколько в среднем каждое значение отличается от среднего значения. Поскольку отклонения возводятся в квадрат, определенный приоритет при расчете этого показателя отдается большим отклонениям, поэтому среднее квадратическое отклонение всегда больше среднего линейного отклонения. Как и в случае среднего линейного отклонения - среднее квадратическое отклонение будет типичным размером отклонений лишь в том случае, если распределение симметрично или близко к нему.

Для качественного альтернативного признака , его дисперсия равна , а среднее квадратическое отклонениегдеw- доля единиц с определенным свойством.