
- •Курс лекций Лекция 1 : Предмет математической статистики. Статистические ряды распределения
- •1.1. Какие закономерности познает математическая статистика
- •1.2 Основные понятия и термины математической статистики
- •1.2.1 Статистическая совокупность
- •1.2.2 Признаки и их классификация
- •2.1 Ранжированный ряд распределения
- •2.1.1 Сущность ранжированного ряда распределения .Табличное и
- •2.1.2 Аналитические возможности ранжированного ряда распределения.
- •2.2 Вариационные ряды распределения
- •2.2.1. Вариационный ряд распределения для дискретного призна
- •2.2.2 Интервальный вариационный ряд распределения
- •2.2.3 Вариационный ряд распределения по качественному признаку
- •2.2.4 Аналитические возможности вариационных рядов распределения
- •2.2.5 Распределение накопленных частот
- •1.1. Система показателей для количественной характеристики статистических распределений.
- •1.2.1 Виды показателей центральной тенденции
- •1.2.3 Средняя гармоническая
- •1.2.4 Средняя геометрическая
- •1.2.5 Мода и медиана
- •1.3 Показатели вариации
- •1.3.1 Размах вариации
- •1.3.2 Среднее линейное отклонение
- •1.3.3 Объем вариации, дисперсия, стандартное отклонение
- •1.3.4 Коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации.
- •1.3. 5 Математические свойства показателей вариации
- •1.4 Показатели ассиметрии распределения
- •1.5 Показатели эксцесса распределения
- •2.1 Закон сложения ( разложения ) вариации
- •2.2 Показатель эффективности разбиения на группы
- •1.1. Сущность и необходимость использования выборочного наблюдения
- •1.2 Основные понятия выборочного наблюдения
- •2.1 Ошибки систематические и случайные
- •2.2 Конкретная, средняя и предельная ошибки выборки
- •3.1 Два типа задач решаемых на основе выборочного метода.
- •3.4 Определение вероятности появления заданной ошибки
- •1.2 Общая схема проверки гипотез
- •2.1 Проверка гипотез относительно средних по данным двух независимых выборок
- •2.2 Проверка гипотезы относительно средней по данным двух зависимых выборок
- •2.1 Конкретизация результатов дисперсионного анализа
- •2.2 Модели дисперсионного анализа
- •1.3 Интерпретация коэффициентов уравнения связи
- •2.1 Показатели тесноты связи
- •2.2 Оценка выборочных показателей связи
- •К расчету показателей центральной тенденции
- •Вначале необходимо составить макет таблицы, внося туда результаты построения интервального ряда (занятие 1) и произвеcсти необходимые расчеты таб.3.1 )
- •Условие: имеются данные интервального ряда распределения (таб. 1.3)
- •1.Интервальная оценка генеральной средней и доли
- •3. Определение вероятности появления заданной ошибки
- •1.Интервальная оценка генеральной средней
- •3. Определение вероятности появления заданной ошибки
1.3 Интерпретация коэффициентов уравнения связи
Раскроем
содержание
полученных коэффициентов уравнения.
Если подойти формально математически
, то коэффициент а
– это значение результативного
признака у
при х=0.
Однако любое уравнение корреляции
строится ,как уже говорилось , на основе
некоторых эмпирических данных , поэтому
а – это
у при х=0 лишь в том случае если
факторный признак х
принимает
или может принять это значение. Иными
словами прежде чем интерпретировать
а надо
определить так называемую область
существования
корреляционного уравнения связи.
Область существования корреляционного
уравнения связи ограничивается
максимальным и минимальным значениями
факторного признака
![]() Если Х=0 входит в область существования,
только в этом случае можно говорить,
чтоа
– это значение результативного
признака у
при х=0.
Если же Х=0 находится вне области
существования, то а
является
неким условным началом и содержательной
интерпретации не подлежит. Коэффициент
в получил
название коэффициента регрессии .
Он показывает ( в случае линейной связи
) на сколько в
среднем изменится
результативный признак при изменении
факторного на единицу. Если изучается
связь между двумя признаками ( один
результативный, другой факторный ) ,
то такая корреляция носит название
парной и коэффициент в
в этом
случае называется коэффициентом полной
регрессии, который отражает влияние
фактора, игнорируя то обстоятельство,
что влияние могут оказывать и другие
факторы. Если изучается связь
результативного признака с несколькими
факторами, то такая корреляция
называется множественной и коэффициенты
(
Если Х=0 входит в область существования,
только в этом случае можно говорить,
чтоа
– это значение результативного
признака у
при х=0.
Если же Х=0 находится вне области
существования, то а
является
неким условным началом и содержательной
интерпретации не подлежит. Коэффициент
в получил
название коэффициента регрессии .
Он показывает ( в случае линейной связи
) на сколько в
среднем изменится
результативный признак при изменении
факторного на единицу. Если изучается
связь между двумя признаками ( один
результативный, другой факторный ) ,
то такая корреляция носит название
парной и коэффициент в
в этом
случае называется коэффициентом полной
регрессии, который отражает влияние
фактора, игнорируя то обстоятельство,
что влияние могут оказывать и другие
факторы. Если изучается связь
результативного признака с несколькими
факторами, то такая корреляция
называется множественной и коэффициенты
(
![]() )
в уравнении
)
в уравнении
![]() получили
название коэффициентов
чистой
регрессии
, которые
показывают насколько в среднем
изменится величина результативного
признака при изменении соответствующего
фактора на 1, при условии , что влияние
других факторов включенных в уравнение
учтено.
получили
название коэффициентов
чистой
регрессии
, которые
показывают насколько в среднем
изменится величина результативного
признака при изменении соответствующего
фактора на 1, при условии , что влияние
других факторов включенных в уравнение
учтено.
Коэффициенты
регрессии являются величинами
именованными, имя их определяется
именами результативного и факторного
признаков. Вследствие сказанного ,
коэффициенты чистой регрессии между
собой не сопоставимы. Сопоставимы
между собой стандартизированные
коэффициенты регрессии:
![]() -
коэффициенты ( бета- коэффициенты ) и
коэффициенты эластичности . Алгоритмы
их расчета следующие :
-
коэффициенты ( бета- коэффициенты ) и
коэффициенты эластичности . Алгоритмы
их расчета следующие : : , где
: , где![]() -
бета – коэффициент поi-
му фактору ;
-
бета – коэффициент поi-
му фактору ;![]() - коэффициент чистой регрессии по
этому фактору ;
- коэффициент чистой регрессии по
этому фактору ;![]() - средние квадратические отклонения
соответственно поi-ому
факторному признаку и признаку
результативному ; Эi
=
- средние квадратические отклонения
соответственно поi-ому
факторному признаку и признаку
результативному ; Эi
=![]()
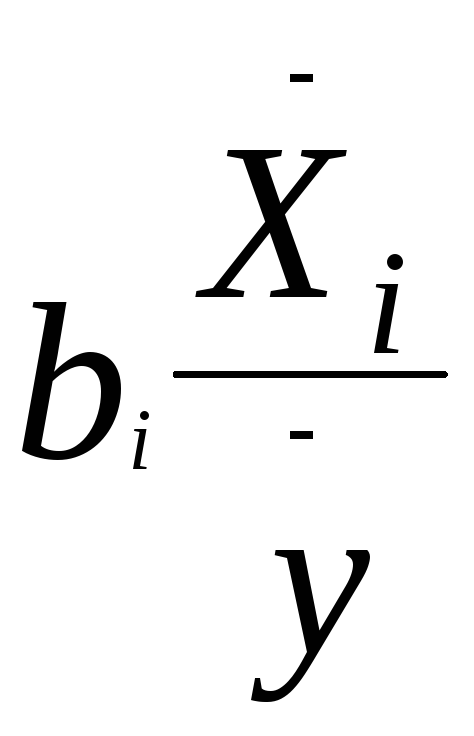 , где Эi-
коэффициент эластичности по i
–ому фактору,
, где Эi-
коэффициент эластичности по i
–ому фактору,
![]() -
коэффициент регрессии по поi
–ому фактору,
-
коэффициент регрессии по поi
–ому фактору,
 средние значения соответственно поi
–ому фактору и результативному
признаку.
средние значения соответственно поi
–ому фактору и результативному
признаку.
![]() -
бета – коэффициент показывает насколько
своих средних квадратических отклонений
в среднем изменится результативный
признак при изменении соответствующего
фактора на свое среднее квадратическое
отклонение. Коэффициент эластичности
показывает на сколько долей (процентов
) в среднем изменится результативный
признак при изменении соответствующего
фактора на долю ( процент ). По величине
стандартизированных коэффициентов
регрессии можно судить о степени
влияния соответствующего фактора на
результат .
-
бета – коэффициент показывает насколько
своих средних квадратических отклонений
в среднем изменится результативный
признак при изменении соответствующего
фактора на свое среднее квадратическое
отклонение. Коэффициент эластичности
показывает на сколько долей (процентов
) в среднем изменится результативный
признак при изменении соответствующего
фактора на долю ( процент ). По величине
стандартизированных коэффициентов
регрессии можно судить о степени
влияния соответствующего фактора на
результат .
Вопросы для повторения по модульной единице 1
18-1 В чем состоит отличие корреляционной связи от функциональной 7
18-2 Каковы этапы построения корреляционного уравнения связи ?
18-3 Какие существуют требования к признакам и совокупности при построении уравнения связи ?
18-4 Как выбрать вид уравнения связи ?
18-5 Каким методом определяются коэффициенты уравнения ?
18-6 Каково содержание коэффициентов уравнения ?
18-7 В чем отличие коэффициентов полной и чистой регрессии ?
18-8 Какие существуют стандартизированные коэффициенты регрессии ?
18-9 Каков алгоритм расчета стандартизированных коэффициентов регрессии ?
Резюме по модульной единице 1
В природе и обществе в силу многочисленных взаимосвязей и зависимостей присутствует прежде всего корреляционная связь. Квалифицированное построение уравнение связи предполагает установление причинно- следственных отношений, а также строгое выполнение требований к факторным признакам и к совокупности по которой строится уравнение связи.
Модульная единица 2 Показатели тесноты связи. Оценка выборочных показателей связи
Целью изучения данной модульной единицы является уяснения содержания термина « теснота связи» освоение алгоритмов расчета показателей тесноты связи и алгоритмов проверки гипотез относительно уравнения связи и показателей связи.
