2.1 Конкретизация результатов дисперсионного анализа

Принятие по критерию F –Фишера альтернативной гипотезы означает, что из всех имеющихся m средних хотя бы две не равны между собой. Это означает , что альтернативная гипотеза принимается , когда из всех средних только две не равны между собой и тогда, когда все m средних обнаружат неравенство. То есть альтернативная гипотеза имеет весьма значительный элемент неопределенности. Устранить этот элемент неопределенности можно конкретизировав результаты дисперсионного анализа, уточнив какие именно средние не равны между собой, а какие возможно остаются равными. Конкретизация результатов дисперсионного анализа может быть произведена с использованием различных критериев. Если число наблюдений по группам ( выборкам одинаково ), то в качестве такого критерия можно воспользоваться критериемQ- Тьюки . Использование критерия Q - Тьюки в целях конкретизации включает следующие шаги :

1. Рассчитываются средние значения признака по группам (выборкам )

, …...

2) Полученные средние ранжируются , например ранжированный ряд может выглядеть так : ,…..

3) Находятся разности первого порядка, под которыми понимаются

разности между средними соседними в ранжированном ряду, например, -;и так далее.

4)Находятся разности второго порядка, то есть разности между средними стоящими в ранжированном ряду через одну позицию, то есть

-,и так далее.

5) Находятся разности следующих порядков , если для этого имеются необходимые средние

6) Относительно каждой из разностей выдвигаются две гипотезы : нулевая ( Н0 ) –в генеральной совокупности разность равна 0 ( нулю ) иными словами в генеральной совокупности соответствующие средние равны между собой и альтернативная (НА ) - в генеральной совокупности разность нулю не равна, то есть соответствующие генеральные средние не равны между собой .

7 ) Для каждой разности находится ее средняя ошибка по формуле :

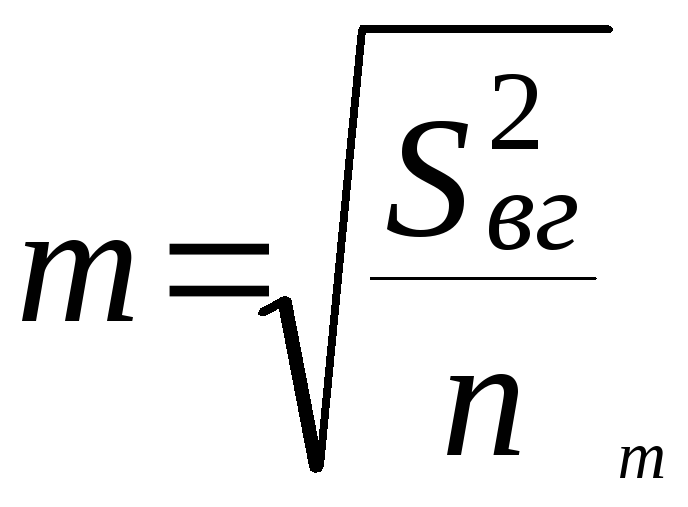, где - внутригрупповая дисперсия,- число наблюдений в каждой группе ( выборке ).

8) Каждую из разностей первого порядка разделим на среднюю ошибку ,получим фактические значения критерия Q-Тьюки для разностей первого порядка , то есть ,и так далее. Полученные фактические значения критерияQ-Тьюки следует сравнить с табличным , которое для всех разностей первого порядка одинаково. Табличное значение критерия Q-Тьюки зависит от уровня значимости, числа степеней свободы внутригрупповой вариации и от величины k , которая для разностей первого порядка равна 2 . Сравнение позволяет принять относительно пары средних или нулевую гипотезу ( средние равны между собой ) или альтернативную гипотезу ( средние составляющие пару не равны между собой )

9) Каждую из разностей второго порядка разделим на среднюю ошибку и получим фактические значения критерия Q-Тьюки для разностей второго порядка. Все фактические значения критерия Q-Тьюки сравниваются с одним и тем же табличным , которое зависит от принятого уровня значимости, числа степеней свободы внутригрупповой вариации и величины k , которая для разностей второго порядка равна 3. Сравнение даст основание для принятия нулевой ( равенство средних ) или альтернативной

( неравенство средних ) гипотезы.

Аналогичная процедура осуществляется относительно разностей третьего, четвертого и так далее порядков, что в конечном счете позволит решить задачу конкретизации дисперсионного анализа.

Равенство или неравенство двух средних может быть установлено путем сравнения их разницы с НСР, которая в данном случае определяется по формуле : НСР =Qтабл mВ связи с изменениемQтабл в зависимости от того какого порядка разность, НСР также меняется. Если фактическая разность между средними меньше или равна НСР, то в генеральных совокупностях эти средние равны между собой. Если же фактическая разность больше НСР , то генеральные средние не равны между собой.