Б. Расчеты с использованием Мастера функций

Выше приведенные методы расчета статистических показателей неудобны, так как для каждого из них необходимо вручную прописывать формулы. Поэтому для удобства работы в программе Excel предусмотрен мастер функций, позволяющий вводить их в полуавтоматическом режиме и практически без ошибок. Многие статистические показатели выборки и параметры генеральной совокупности можно очень быстро определить с помощью функций, тем более что наименование большинства функций совпадает с наименованием статистических показателей.

В Листе 1 файла Книга1 в столбце введем, символ Х и значения глубины вспашки по 8-ми точкам. В ячейки с А10 по А17 впишем наименование статистических показателей, которые приведены в работе 1.

Для определения средней выборочной (средняя арифметическая) активизируем ячейку В10 (выделенная ячейка со знаком =), в этой ячейке будут отображаться результаты наших вычислений. Для вызова мастера функций необходимо нажать кнопкуВставка функциина стандартной панели инструментов или на строке формул нажать на «fx».

Появляется контекстное меню «Мастер функций – шаг 1 из 2, в категории выбрать «Статистические» (рис. 2.12. )

Рис.2.12. Лист с исходными данными и контекстным меню «Мастер функций»

После выбора категории « Статистические».в окне появляется перечень конкретных статистических функций, выбираемСРЗНАЧ, что означает среднюю по выборке (рис. 2.13 ).

Рис. 2.13. Выбор функции СРЗНАЧ

Далее открывается окно для выбора аргументов функции. В поле Число 1ставим курсор и мышкой выбираем диапазон значений глубины вспашкиВ2:В9, нажимаем клавишуОК, в строке формул автоматически появляется наименование функции и диапазон ячеек(=СРЗНАЧ(В2:В9), а в ячейкеВ10появляется в скобках этот же диапазон (рис. 2.14 )

Рис. 2.14. Диалоговое окно для выбора аргументов функции.

После нажатия клавиши ОКили щелчка мышки в ячейкеВ10появляется значение выборочной средней – средняя глубина вспашки –20,25 см. (рис. 2.15 )

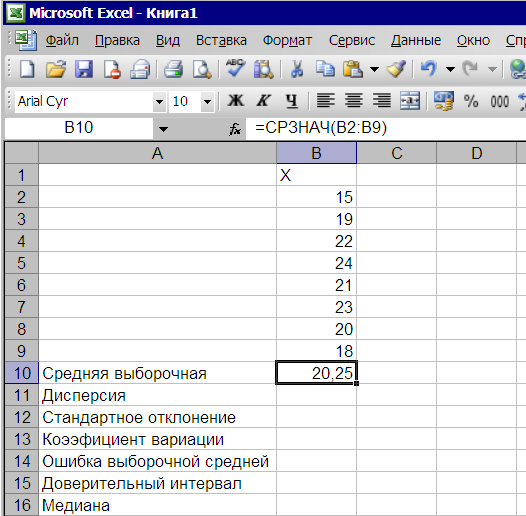
Рис.2.15. Средняя глубины вспашки – средняя выборочная – 20,25 см.

Находим объем выборки (n), который в Мастере функций называется счет (рис. 2.16)

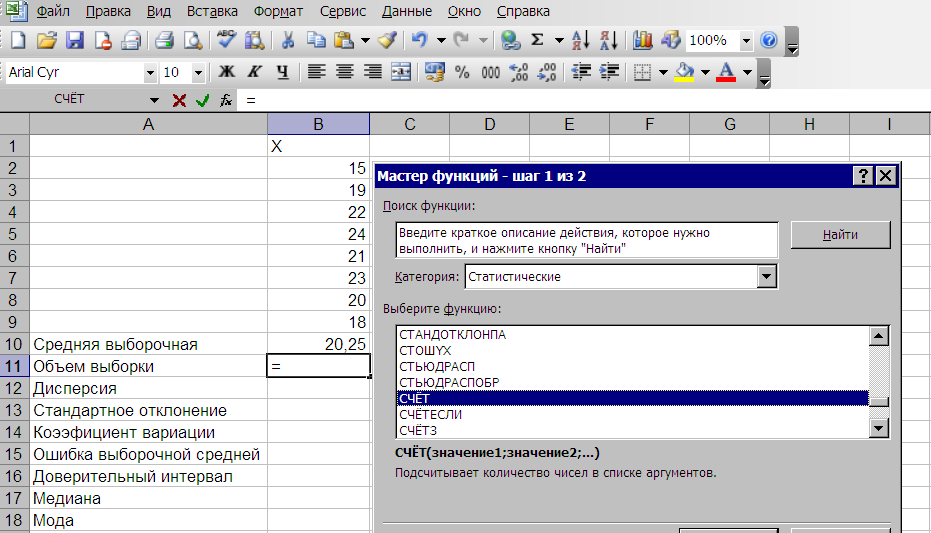
Рис.2.16. Диалоговое окно для нахождения объема выборки (счет)

Выбираем из списка функций ДИСП– дисперсия для выборки. Обратите внимание на то, что в списке имеетсяДИСПР – дисперсия для генеральной совокупности. При выборе конкретной дисперсии в подсказке указывается, что оценивает данная дисперсия (рис. 2.17 ).

Рис. 2.17. Диалоговое окно для выбора дисперсии

Для расчета дисперсии в поле Число 1ставим курсор и мышкой выбираем диапазон значений глубины вспашкиВ2:В9, нажимаем клавишуОК (рис.2.18)

Рис. 2.18. Выбор диапазона ячеек для определения дисперсии

Выбираем из списка функций СТАНДОТКЛОН– стандартное отклонение для выборки. Точно также как и для дисперсии в списке имеетсяСТАНДОТКЛОНП – стандартное отклонение для генеральной совокупности. При выборе конкретного стандартного отклонения в подсказке указывается, что оценивает данное стандартное отклонение (рис. 2.19 ).

Рис. 2.19. Диалоговое окно для выбора стандартного отклонения

В списке как математических, так и статистических функций нет такой функции с помощью, которой можно рассчитать коэффициент выборки (V), поэтому воспользуемся уже известной процедурой ручного набора формул.

Коэффициент вариации представляет собой отношение стандартного отклонения к выборочной средней, выраженной в %. Выделим ячейку для формулы коэффициента вариации В14, затем в строке формул пропишем формулу со ссылкой на ячейки, где находятся стандартное отклонение и выборочная средняя –(В13/В10*100)(рис. 2.20 )

В итоге получаем коэффициент вариации (V) = 14,3974%.

Рис. 2.20. Формула для определения коэффициента вариации

Расчет ошибки выборочной средней

Так как в списке функций нет очень важного статистического показателя – ошибки выборочной средней (стандартная ошибка), рассчитаем этот важный показатель с помощью формул. Выделим ячейку для размещения формулы и получения готового результата В15 , затем в строке формул сначала вставим символ=и укажем следующую формулу:В13/КОРЕНЬ (В11). В ячейкеВ13 значение стандартного отклонения, в ячейкеВ11– объем выборки. После нажатия на клавишуEnter в ячейкеВ15получаем результат –1,0307764.(рис. 2.21)

Рис. 2.21. Расчет ошибки выборочной средней

Расчет предельной ошибки выборочной средней для нахождения доверительного интервала генеральной средней. Предельная ошибка выборочной средней представляет собой произведение критерия Стьюдента на ошибку выборочной средней (t ₀₅*S_x). Значение критерия Стьюдента зависит от числа степеней свободы (n – 1) .

В Мастере функций для нахождения предельной ошибки средней выборочной имеется функция, которая имеет странное название ДОВЕРИТ. Поместим курсор в ячейкуВ16 . затем из списка статистических функций выберем функциюДОВЕРИТ (рис. 2.22 ), нажимаем ОК.

Рис. 2.22. Выбор в меню функции ДОВЕРИТ (предельная ошибка средней)

В появившемся диалоговом окне вводим:

- в поле Альфа введем уровень значимости –0,05,

- в поле Станд_откл. – ссылку на ячейку, где находится стандартное отклонение или готовое значение (2,915),

- в поле Размер – объем выборки (8)

После нажатия на клавишу ОК получаем результат – предельная ошибка выборочной средней равна2,019 (рис. 2.23)

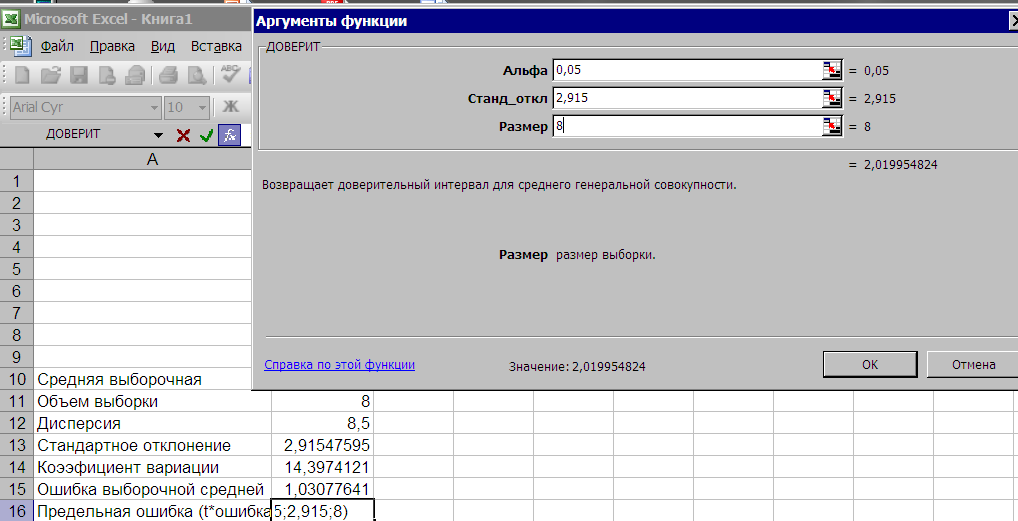
Рис. 2.23. Расчет предельной ошибки выборочной средней

95%-й доверительный интервал (ДИ) для генеральной средней ():

В ячейке А17вводим текст «Доверительный интервал», в ячейкуВ17 записываем значения ДИ следующим образом:20,25 ± 2.02(рис. 2.24 )

Для вычисления медианы – ячейка В18 выбираем функциюМЕДИАНА, в следующем окне указываем диапазонВ2:В9 и в итоге получаем значение –20,5

На рис. 2.24 показаны результаты расчета основных статистических показателей 50 клубней картофеля по массе, г. (Работа 2)

Рис. 2.24. Основные статистические показатели выборки - 50 клубней картофеля