Арифметические операторы

• «+» — сложение (Пример: «=1+1»);

• «-» — вычитание (Пример: «=1-1»);

• «*» — умножение (Пример: «=2*3»);

• «/» — Деление (Пример: «=1/3»);

• «^» — Возведение в степень (Пример: «=2^10»);

• «%» — Процент (Пример: «=3 %» — преобразуется в 0,03; «=37*8 %» — нашли 8 % от 37). То есть если мы дописываем после числа знак «%», то число делится на 100.

Результатом вычисления любого арифметического выражения будет число

Логические операторы

• ">" — больше;

• "<" — меньше;

• ">=" — больше, либо равно;

• "<=" — меньше, либо равно;

• "=" — равно (проверка на равенство);

• "<>" — неравно (проверка на неравенство).

Функции в Microsoft Excel

В формулах Microsoft Excel можно использовать функции. Сам термин «функция» здесь используется в том же значении, что и «функция» в программировании. Функция представляет собой готовый блок (кода), предназначенный для решения каких-то задач. Функции - это встроенные инструменты, которые применяются в формулах. В Microsoft Excel имеется большое число стандартных функций. Они используются как для простых, так и для сложных вычислений. Каждая функция имеет свое название. Все функции разделены на 12 категорий, наибольший интерес представляют математические и статистические (рис. 1.5.).

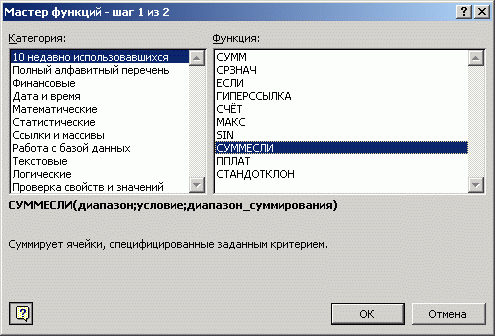
Рис.1.5. Диалоговое окно Мастер функций

 

2. Определение основных статистических показателей выборки (Работа 1) в программе Excel

Работа 1. Произведено измерение глубины вспашки (X, см) в 8 точках (n=8). Необходимо рассчитать основные статические показатели выборки

Значение признака, Х,см	От нуля (А=0)
		2
15 19 22 24 21 23 20 18
Суммы	=	2=

Основные статистические показатели (характеристики) выборки

Выборочная средняя

Поправка

Сумма квадратов =–С =

Дисперсия

Стандартное отклонение

Коэффициент вариации

Ошибка выборочной средней

95%-й доверительный интервал (ДИ) для генеральной средней ():

95%-й доверительный интервал (ДИ) для всей совокупности (любого значения Х):

Медиана – центральное значение ранжированной выборки: Ме

Статистические расчеты в программе Excel можно провести 3 способами:

- Ввод формул в строке формул

- Использование Мастера функций

- Использование встроенного Пакета данных

Расчеты с использованием формул

Решение: 1. После запуска программы Excel в Лист 1 заносим таблицу исходных данных, для чего в ячейке В1 введем символ Х, в ячейке С1 – Х^2 , что означает Х² , а в ячейках столбца В – значения глубины вспашки по 8 точкам. (рис. 2.1. )

Рис. 2.1. Исходные данные по глубине вспашки

2. Для расчета сумм квадратов отклонений необходимо, прежде всего, возвести каждое число в квадрат, а затем найти сумму квадратов. Чтобы возвести в квадрат число 15 и полученное значение записать в ячейку С2, необходимо (рис. 2.2.):

- левой клавишей мыши одни кликом активизировать ячейку С2,

- в строке формул нажмите кнопку со знаком равенства =

- в строке формул после знака равенства =ввести формулуВ2^2

При этом введенная формула автоматически отображается в ячейке С2 и одновременно синим цветом выделяется контур ячейкиВ2. (рис. 2.2.)

Рис. 2.2. Формула – возведения в квадрат

После нажатия на клавишу Enter или нажатия на левую клавишу мыши формула закрепляется для данной ячейки и в ячейке С2 получаем результат возведения в квадрат 15 – 225. (рис.2.3. ) Теперь, при введении любого значения в ячейкуВ2, в ячейкеС2 будет получен квадрат этого числа.

Рис. 2.3. Квадрат числа значения ячейки В2в ячейкеС2(225).

Для возведения в квадрат последующих данных в квадрат можно было бы повторить вышеуказанную процедуру по всем строкам. Однако, это займет много времени и эту операцию намного проще и быстрее выполнить на простом калькуляторе.. В программе Excelесть замечательная функция «Перенос» с помощью которой очень быстро возвести в квадрат любой массив данных.

С помощью мыши активизируем ячейку С2, левой клавишей подводим к нижнему правому углу выделенного прямоугольника ячейки, появляется значок+, закрепляем левой клавишей мыши и нажимая на нее, выделяем диапазон ячеекС2:С9 (Рис. 2.4. ) – в выделенных ячейках получаем квадраты по всем значениям.

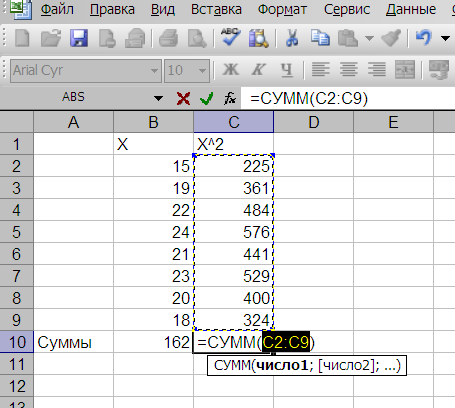
Рис. 2.4. Возведение в квадрат и суммирование

Теперь необходимо определить в ячейке В10суммы значений Х и в ячейкеС10суммы квадратов Х². Для определения сумм воспользуемся значком ∑ из строки инструментов и затем последовательно выделим диапазоны ячеек с цифрами по столбцамВ2:В9 и С2:С9 (Рис. 2.4 )

Добраться до формулы можно по-разному. Вначале нужно выделить ячейку, в которой будет стоять формула. Саму формулу можно прописать вручную в строке формул либо воспользоваться ее наличием на панели задач – закладка «Главная», справа вверху есть разворачивающаяся кнопка со значком суммы Σ (рис. 2.5) . После вызова формулы в скобках потребуется прописать диапазон данных С2:С9, по которым будет рассчитываться сумма. Сделать это можно мышкой, нажав левую клавишу и протянув по нужному диапазону.

Рис. 2.5. Знак суммирования

В итоге получаем: ∑X= 162 и ∑X² = 3340 (рис. 2.6. )

Рис. 2.6. Сумма значений Х и сумма квадратов Х².

Далее необходимо рассчитать поправку (). Для этого активизируем ячейкуВ11, . затем в строке формул записываем формулуB10^2/8 (рис 2.7. ) и итоге получаемС= 3280,5

Рис. 2.7. Расчет поправки

В строку А12 введем текст «Сумма квадратов отклонений» (рис.2.8. )

Рис.2.8. Текст «Сумма квадратов отклонений» в ячейке А12

Несмотря на то, что в каждую отдельную ячейку можно ввести до 32000 символов, после введения больших текстов и перевода курсора в другую ячейку, в первой ячейке видна только часть текста. Поэтому каждую ячейку или столбец можно раздвинуть вправо или сформатировать ячейку, указав на перенос слов. Для того, чтобы расширить ячейку А12, наведите курсор мыши в шапке между столбцами А и В, курсор изменяет форму. Появится значок «прямоугольный крест» Зажмите левую кнопку мыши и, не отпуская ее, переместить курсор вправо, будет изменяться ширина столбца А. (рис.2.9. )

Рис.2.9. Ширина столбца после изменения.

Расчет сумм квадратов отклонений =–С = произведем в Excel следующим образом. В строку формул введем формулу со ссылками: сумма квадратов (С10) – поправка (В11) и в результате получаем сумму квадратов – 59,5 в ячейке В12 (рис.2.10)

Рис. 2.10. Расчет сумм квадратов отклонений

Дисперсия . Для расчета дисперсии в строку формул введем формулу В12/7 и в итоге в ячейке В13 получаем значение дисперсии –8,5 (рис. 2.11.)

Рис.2.11. Расчет дисперсии